大数の法則の視覚化から理想の推定量を考える

概要

シミュレーションで「大数の法則」を視覚的に表しながら説明してみる.
推定量の「一致性」「不偏性」「有効性 (効率性)」とはなんなのかも説明
異なる性質を持つ推定量が大数の法則のもとでどういう違いが出るのかを視覚的に表す.
というか中心極限定理の視覚化 (【統計学】中心極限定理のイメージをグラフで掴む - Qiita とか可視化で理解する中心極限定理 #rstatsj - Qiita) に影響された.

2015/5/11 最後の具体例について続編を書きました

図: 算術平均と不偏性・有効性を満たさない推定量の比較

f:id:ill-identified:20150504230712p:plain

大数の法則

まず, 大数の法則 (Law of Large Numbers) についてのおさらいになる.

なにかの数値を集計して全体的な傾向を考えるとき, われわれは深く考えずに $(1+2+3+\cdots)/N$ のように $N$ 個の数を足して $N$ で割る「算術平均」を用いているが, 母集団のすべての情報を得ているわけではない場合でも, なんとなく算術平均をもとに, 全体の平均がそうであると解釈している.

しかし実際には, そのような場合でも「大数の法則」によって算術平均が非常にすぐれた指標であることが分かっている. ある $X$ という変数が, 平均 $\mu$ の分布に従うとする. この $X$ というのは, 母集団全体について, 代表して特徴を表す未知の法則で, $\mu$ はその特徴を表す指標 (母数; パラメータ) と考える (特に母集団の平均なので, 「母平均」と呼ばれる.). この未知の数値をいくつかの観測によるデータ (サンプル) を用いて推定するのが統計推測である. 大数の法則とは, この母集団から標本として取り出した $N$ 個の値 $X_{1},X_{2},\,\cdots,\, X_{N}$ の算術平均 (標本平均)

$\begin{align} \bar{X}_{N}= & \frac{X_{1}+\cdots+X_{N}}{N}\end{align}$

について,

$\begin{align} \lim_{N\to\infty}\bar{X}_{N}= & \mu\end{align}$

が成り立つという定理である. つまり, サンプルサイズである $N$ が増えれば増えるほど, 算術平均は母平均 $\mu$ の値に近づく. 算術平均というとありふれたもののように聞こえるが, 算術平均もれっきとした「推定量」の1つである. そして, 大数の法則では, $X_{1},\, X_{2},\,\cdots$ がすべて互いに独立で, かつ同一の分布にしたがう必要がある (同じ $X$ という法則から取り出した値なので, 同一の分布に従うと考えるのは自然である) が, どのような分布かは条件を課していない. よって, 正規分布でもポアソン分布でも, (平均さえ定義できるなら) どんな分布のデータに対しても大数の法則は適用できる.

厳密には, 大数の法則は「弱法則」と「強法則」があり, 今紹介したのは弱法則で, 証明*1も比較的簡単である. しかし, 今回は証明を見せられてもいまいちよく分からない, という人のために, シミュレーションで視覚的に大数の法則を表現する.

シミュレーションといっても大したものではない. 擬似的なサンプルとして, 平均10, 分散1の正規分布 *2にしたがう乱数を大量に作成する. つまり, 母集団の分布が標準正規分布なので, 母平均 $\mu$ は10である. そこで, 算術平均を計算するための乱数の数をすこしづつ増やして, 横軸に $N$ を, 縦軸に $\bar{X}_{N}$ をとって, 実際に真の値に近づいているのかを確認する. せっかくなので, 10000個の乱数を10パターン作成して, それぞれの算術平均の推移を表すことにした.

これがその結果である.

図1: 大数の法則によって収束する算術平均

f:id:ill-identified:20150504225340p:plain

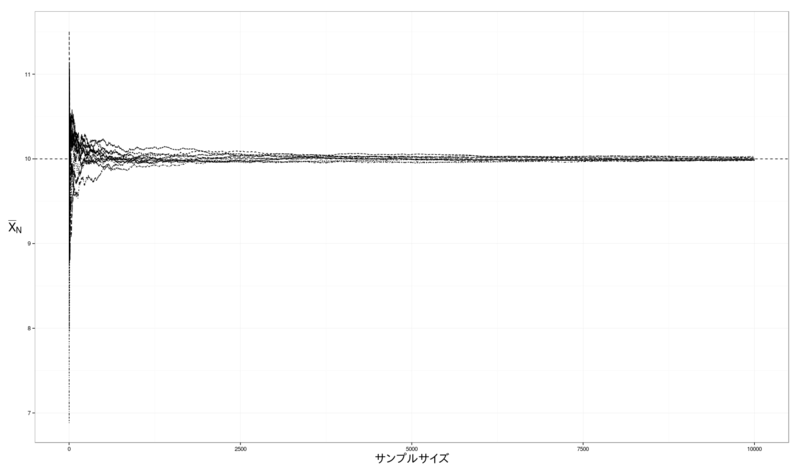
しかし, 収束のスピードは $N$ に対して線形でないので, 最初のうちは非常に振れ幅が大きい. そこで, 見やすくするために横軸を対数尺度にしてグラフを作り直す.

図2: 対数尺度で表した場合

f:id:ill-identified:20150504231052p:plain

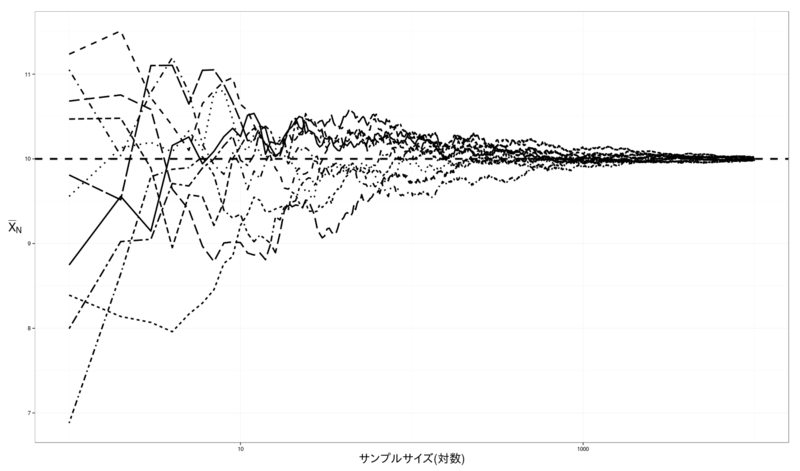
図2 から, サンプルサイズの小さいうちは真の値の上下に大きく振れながら動き, サンプルサイズの増加によってしだいに真の値に近づいていく様子がわかる.

図1, 2 は以下のコードで作成した. ggplot2, reshape2, ggthemes パッケージさえインストールされていれば特に下準備は必要ない. また, 5行目で set.seed() 関数を使っているのは擬似乱数を固定し, 全く同じグラフを作るためである. この1行を消して, 違う乱数で繰り返し試してもよい.

# 本体 ver. 3.2.0
library(ggplot2)  # ver. 1.0.1 グラフ作成に必要
library(ggthemes) # ver. 2.1.2 ggplot2のデフォルトのカラーパレットが毒々しすぎるので
library(reshape2) # ver. 1.4.1 データフレームの加工用
set.seed(1)
size <- 10^4 # 乱数の数
ser <- 10 # 系列の数
m <- 10 # 母平均
df <- data.frame(N=1:size)
X    <- matrix(rnorm(n=size*ser, mean = m),ncol = ser) # 10通りの原系列作って比較
avgs <- data.frame(apply(X,2,function(x){cumsum(x)/1:size}) )
colnames(avgs) <- paste("avg", 1:ser, sep ="")
df <- cbind(df,avgs)
df.melt <- melt(df, measure.vars=colnames(df)[-1])
# グラフ作成
(
LLN <- ggplot(data=df.melt) + geom_path(aes(x=N,y=value, group=variable, linetype=variable)) +
    geom_hline(yintercept = m, linetype="dashed") +
    labs(x="サンプルサイズ", y=expression(bar(X)[N])) +theme_bw() +
    theme(axis.title= element_text(size=20), axis.title.y = element_text(angle = 0, hjust = .5)) +  scale_linetype_discrete(guide=F)
)
# 対数尺度に
(LLN2 <- LLN + scale_x_log10() + labs(x="サンプルサイズ(対数)"))

一致性・不偏性・有効性

一致性

サンプルサイズ $N$ が無限大になったとき, 母数の真の値に収束するような性質を一致性 (consistency) といい, そういう推定量を一致推定量と呼ぶ. 一致性があるかどうかは, ほとんどの場合, この大数の法則をもとに判断できる. ここまでの話から, 算術平均はあきらかに母平均の一致推定量になる.

実際には, 「無限大のサンプル」というものは存在しない. 現実的にはサンプルサイズ $N$ は必ず有限である. が, サンプルサイズが十分に大きければ, 真の値との誤差の大きさも気にするほどのことではなくなると言える.

しかし, それでもなお, この, 「十分なサンプルサイズ」が手に入らない場合もある. 何にもまして, 一致性のある推定量を使うのが大前提だが, 一致性だけでは信頼できる推定をすることはできない. そこで, 一致性以外の性質についても考える必要が出てくるのだ.

不偏性

まず, 不偏性 (unbiasedness) とは, 算術平均で言えば, 算術平均の期待値が母平均に等しい, つまり

$\begin{align} \mathrm{E}\bar{X}_{N}= & \mu\end{align}$

であることをいう. 「平均の期待値」というのがもしかするとわかりづらいかもしれないが, サンプルの個々の観察値 $X_{1},\, X_{2},\,\cdots,$ もなんらかの分布に従っている以上, それらの和に定数 $N^{-1}$ を掛けた算術平均も何らかの分布に従っているので, $\bar{X}_{N}$ をひとつの確率変数と考えると, 期待値が存在することになる.

不偏性は, $N$ の大きさについて言及がない. つまり, $N$ が小さくても, 常に期待値が真の値と一致する性質である. そして, 算術平均はこの不偏性をもつ不偏推定量でもある. 証明はやはり省略する*3.

有効性

一致性と不偏性のある推定量でも, 有効性 (efficiency) を持つかどうかは分からない. 有効性とは, あらゆる不偏推定量の中で*4, その推定量の分散が $N$ によらず最小である*5ということである.

$\begin{align} \mathrm{V}(\bar{X}_{N})\leq & \mathrm{V}(\tilde{\mu}),\,\forall\tilde{\mu},N\end{align}$

推定量の分散が小さいということは, 推定量の値と真の値のあいだに誤差がほとんどない可能性が高いことを意味する. 推定量の分散は, クラメル=ラオ (Cramér-Rao) の不等式により, 下限が存在することが知られている*6. この下限を達成するような推定量が有効推定量である*7. この有効性についても, $N$ の大きさは関係ない. よって, サンプルサイズが小さい場合でも意味のある性質である. なお, 算術平均は有効性も持っているので, 結局, 一致性・有効性・不偏性の3つの条件すべてを満たしている有効不偏一致推定量である.

各推定量を視覚化する

一致推定量

算術平均が推定量として優れた性質を持っていることがわかったので, 逆に有効性や不偏性のない推定量とも比較してみる. まず,

$\begin{align} \hat{\mu}= & \frac{X_{1}+\cdots+X_{N}}{N+1}\end{align}$

という推定量の性質を考える. 算術平均の分母 $N$ を $N+1$ に置き換えただけなので, $N\to\infty$ のとき結局同じだから, $\hat{\mu}$ でも母平均の一致推定量になる. しかし, $X_{1},\,\cdots,\, X_{N}$ が互いに独立であることに注意して $\hat{\mu}$ の期待値を計算すると,

$\begin{align} \mathrm{E}\hat{\mu}= & \frac{1}{N+1}\sum_{i=1}^{N}(\mathrm{E}X_{i})\\ = & \frac{1}{N+1}N\mu\\ = & \frac{N}{N+1}\mu\end{align}$

となるので, 不偏性を満たさない*8. この推定量 $\hat{\mu}$ では, 実際の $\mu$ よりも値が小さくなる傾向 (下方バイアス) がある.

また, この式から, あらためて不偏性と一致性の違いがわかる: $N\to\infty$ のとき, 明らかに右辺は $\mu$ になる. よって, 一致性とは, サンプルサイズが無限のときに限定して不偏性を持つ性質, とも解釈できる*9 *10. では, $\hat{\mu}$ の有効性はどうかというと, 不偏性があるため有効性が満たされない. よって, $\hat{\mu}$ が持つ性質は一致性のみである.

不偏一致推定量

つぎに, 不偏一致推定量で, 有効性を満たさない推定量も用意する. $a_{1},\,\cdots,\, a_{N}$ を正の実数の列とする. 以下のような $\bar{\mu}$ を考える.

$\begin{align} \bar{\mu}= & \frac{a_{1}X_{1}+a_{2}X_{2}+\cdots+a_{N}X_{N}}{a_1 +\,\cdots \,+a_N}\end{align}$

要するに, 加重平均である. ここで, $a_{1},\,\cdots,\, a_{N}$ を全て同じ一定の数 $1/N$ にすると $\bar{\mu}$ は算術平均 $\bar{X}_{N}$ と全く同じになるが, 今は算術平均以外の推定量を考えたいので, このケースは除外する. 加重平均も一致性をもつ (証明は略) し, 期待値をとると

$\begin{align} \mathrm{E}\bar{\mu}= & \frac{\mathrm{E}a_{1}X_{1}+\mathrm{E}a_{2}X_{2}+\cdots+\mathrm{E}a_{N}X_{N}}{a_1 +\,\cdots,\,+a_N}\\ = & \frac{a_{1}\mu+\cdots+a_{N}\mu}{a_1 +\,\cdots,\,+a_N}\\ = & \frac{\mu(a_{1}+\cdots+a_{N})}{a_1 +\,\cdots,\,+a_N}=\mu\end{align}$

なので不偏性も持つ, しかし, 分散を求めると,

$\begin{align} \mathrm{V}(\bar{\mu})= & \mathrm{V}\left(\frac{\sum_{i=1}^{N}a_{i}X_{i}}{\sum_{i=1}^N a_i}\right)\\ = & \frac{1}{N^{2}}\mathrm{V}\left(\sum_{i}a_{i}X_{i}\right)\\ = & \frac{1}{N^{2}}\sum_{i}a_{i}\mathrm{V}(X_{i})\\ = & \sigma^{2}\frac{\sum_{i}a_{i}^{2}}{(\sum a_{i})^{2}}\end{align}$

$\{a_{N}\}$ の定義から, 分数部分は $0<\sum_{i}a_{i}^{2}/(\sum_{i}a_{i})^{2}\leq1$ の範囲にある定数である. 一方で, 有効推定量でもある算術平均の分散は

$\begin{align} \mathrm{V}(\bar{X}_{N})= & \mathrm{V}\left(\frac{\sum_{i=1}^{N}X_{i}}{N}\right)\\ = & \frac{1}{N^{2}}\sum_{i=1}^{N}\mathrm{V}(X_{i})\\ = & \frac{N}{N^{2}}\sigma^{2}=\frac{\sigma^{2}}{N}\end{align}$

である. よって, 有効推定量であるには, 分散が $N$ の増加にしたがって減少する, $\sigma^{2}/N$ でなければならない*11. $\bar{\mu}$ は, $N$ の大きさと $\{a_{i}\}$ の値によっては分散が有効推定量の値以下になるが, 全ての $N=1,\,2,\,\cdots$ に対してこの値になるわけではない. よって, $\bar{\mu}$ は有効推定量ではない. 実際に視覚化するには, $\{a_{N}\}$ の値を決める必要があるので, 今回は $a_{k}=k^{4}$ と適当に決めた.

算術平均 $\bar{X}_{N}$ にくわえて $\hat{\mu},\,\bar{\mu}$ についても収束する様子をグラフ化したのが冒頭のグラフである.

図3: 算術平均と不偏性・有効性を満たさない推定量の比較

まず, 不偏一致推定量だが有効性を持たない $\bar{\mu}$ (青色) は, $\bar{X}_{N}$ (黒色) と同様に真の値に収束していっているが, あきらかに振れ幅が $\bar{X}_{N}$ より大きいことから「分散が大きい」ことが直観的にわかると思う. 次に, $\hat{\mu}$ (黄色) は, $N$ が大きくなるほど真の値に近づいているが, $N$ の小さいうちは大きく下に振れていおり, 斜め下から $\mu=10$ に漸近していっている. これが不偏性を持たない, つまりバイアスのある推定量の性質である. 不偏性を持つ $\bar{X}_{N}$ や $\bar{\mu}$ は, $N$ が小さいうちは振れ幅が大きいものの, $\mu=10$ の上下に「均等に偏っている」ように見える. これに対し, $\hat{\mu}$ は下に偏っている. もちろん, 上側に偏るバイアスをもつ推定量というのも考えられる.

グラフ作成は, 以前のコードに引き続き, 以下のコードの入力で作成できる.

#### バイアス推定量, 非有効推定量との比較 ####

# 一致性があるが不偏性がない (下方バイアス)
biased <- apply(X, 2, FUN =function(x){cumsum(x)/(1:size+1) } )
colnames(biased) <- paste("biased", 1:ser, sep="")
df2 <- cbind(df, biased)

# 有効性がない不偏一致推定量 (適当な加重平均)
uneff   <- apply(X, 2, FUN=function(x){weights <- (1:size)^4;                                        cumsum(x*weights)/cumsum(weights)}) colnames(uneff) <- paste("unefficient", 1:ser, sep="")
df2 <- cbind(df2, uneff)

# ggplot用に加工
df2.melt <- melt(df2, measure.vars = colnames(df2)[-1] )
df2.melt$type <- sub(x= df2.melt$variable, pattern = "^([a-z]+).+",  replacement="\\1")
df2.melt$series <- sub(x= df2.melt$variable, pattern = ".+([0-9]+)", replacement= "\\1")

# グラフ描画
ggplot(data=df2.melt) + geom_path(aes(x=N,y=value, group=variable, linetype=series, color=type)) +
    geom_hline(yintercept = m, linetype="dashed") +
    labs(x="サンプルサイズ(対数)", y=expression(mu)) +theme_bw() +
    theme(axis.title= element_text(size=20), axis.title.y = element_text(angle = 0, hjust = .5), legend.title=element_blank(), legend.text=element_text(size=15)) +
    scale_linetype_discrete(guide=F)+
    scale_x_log10() +
    scale_colour_colorblind(label=c(expression(bar(X)[N]), expression(hat(mu)), expression(bar(mu)) )) # 見やすい色

具体例

最後に, 算術平均の例だと実用性に欠けるので, 視覚化はしないが少し具体例を挙げておく. 最小二乗法から得られる最小二乗推定量も, ある仮定のもとで, 大数の法則によって, 真の値に一致することが分かっている. これが, 最小二乗法が統計学でよく使われる理由の1つである. しかし, この「ある仮定」というのがどんなケースでも常に成り立つとは限らず, 「バイアスのある一致推定量」や「有効性のない不偏一致推定量」を使わざるを得ない場合がある.

時系列データの回帰分析: 時系列データは誤差項が独立でない場合が多い (系列相関). この場合, 最小二乗推定量では不偏性があっても有効性がないことになる. また, 自己回帰モデルなら不偏性もない可能性がある (参考: 沖本, 2010, 経済・ファイナンスデータの計量時系列分析).
→ 続編: [R] 回帰分析で適切な方法を使わないとどうなるか (時系列編) - ill-identified diary
操作変数法: 以前 [GMM] 一般化モーメント法と操作変数 - ill-identified diary で言及したように, 2段階最小二乗法は一致性のみで, 普遍性も有効性も保証されない.
→ 続編: [R] 回帰分析で適切な方法を使わないとどうなるか (操作変数編) - ill-identified diary

参考文献

大谷一博 (2015). 基礎統計分析講義資料. http://www.econ.kobe-u.ac.jp/~ohtani/stat.html

竹村彰通 (1991). 現代数理統計学. 創文社.

沖本竜義 (2010). 経済・ファイナンスデータの計量時系列分析. 朝倉書店.

*1:大数の法則と言ってもいくつかバリエーションがある. 最もよく紹介される弱法則は, マルコフの不等式の特殊形であるチェビショフの不等式から導くことができる「チェビショフ (Chebyshev, Чебышев, ラテン字表記からチェビシェフとも) の弱法則」であり, 強法則はボレル・カンテリの補題から導かれる定理を指すことが多い.

*2:平均10には特に意味はない. 単にゼロ以外のきりの良い数字にしたかっただけである.

*3:この後の有効性についても, あわせて数理統計学の基本的な話なので, 数式で導出過程を知りたい場合, 大谷 (2015, 基礎統計分析講義資料) などを参考に.

*4:不偏性をみたさない推定量は必ず有効性を満たさない

*5:よって, 全ての $N$ に対して分散が最小という意味で, 一様最小分散性とも呼ばれることがある

*6:証明は竹村 (1991, 現代数理統計学) などを

*7:例えば以前科学史から最小二乗法 (回帰分析) を説明してみる - ill-identified diary で言及したように, ガウス=マルコフ定理によれば, 最小二乗推定量の分散はこのクラメル=ラオの下限に等しいので, 有効推定量である.

*8:このような期待値の計算方法は一博 (2015, 基礎統計分析講義資料)を参照

*9:そもそもある一点に収束するので, もはや一般の意味での確率分布ではなくなる

*10:逆に, 漸近的に不偏だからといって一致性を持つとは限らない. サンプルサイズどれだけ増加しても上下に均等に揺れ動いたままいつまでも揺れ幅が小さくならない, という状況なら, 不偏性はなりたつが一致性は成り立たない.

*11: $N\to\infty$ のとき, ある一点に収束するため, 分散はゼロになる. 有効推定量の分散と一致性は整合がとれている