ill-identified diary

所属組織の見解などとは一切関係なく小難しい話しかしません

トップ > 計量経済学 > [R] 回帰分析で適切な方法を使わないとどうなるか (操作変数編)

[R] 回帰分析で適切な方法を使わないとどうなるか (操作変数編)

計量経済学 R 視覚化 教材
この記事は最終更新日から3年以上が経過しています

概要


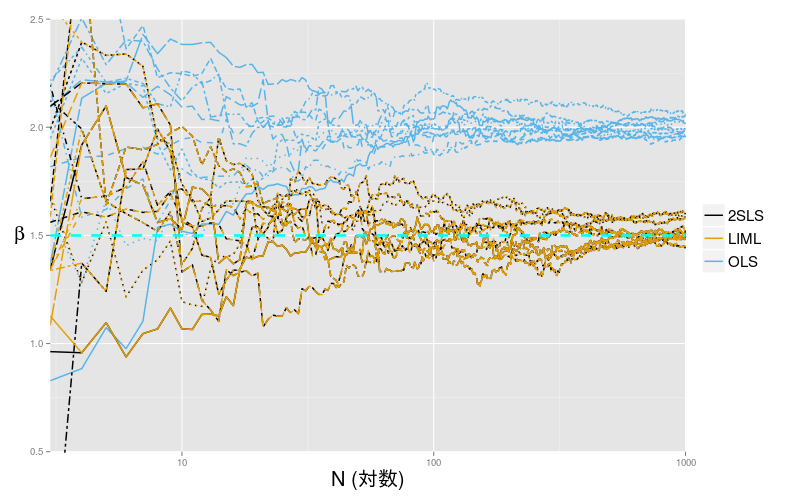
図1: OLS と 2SLS

f:id:ill-identified:20150511194955p:plain

操作変数

前回は大数の法則により, サンプルサイズを大きくすると算術平均が真の平均値に収束すること (一致性), また収束に偏りがないこと (不偏性), 収束のバラつきが小さいこと (有効性) の重要さを説明した. 前回の最後に, 「操作変数法では一致性しか保証されない」 という話をした. そこで, 今回はこれについてもシミュレーションにより視覚化してみた. 操作変数法による推定 (2段階最小二乗推定量) が, 一致性のみ不偏性・有効性を持たないという話の理論的根拠は [GMM] 一般化モーメント法と操作変数 - ill-identified diary などを参照してほしい.

操作変数法について, 簡単な説明だけしておく. 単回帰モデル

\begin{align} y_{i}= & \alpha+\beta x_{i}+\varepsilon_{i}\end{align}

では, 誤差項 \varepsilon_{i} と説明変数 x_{i} が相関していると, 通常の最小二乗法 (OLS) で推定しても, その結果は一致性を持たない. したがって不偏性も有効性もない. よって, 最小二乗法は推定として妥当ではない. こういうとき, 誤差項とは相関しないが, 説明変数 x_{i} と相関する第3の変数 z_{i} があれば, この変数を操作変数として計算に用いる2段階最小二乗法が利用できる. ここから得た結果は, 一致性が保証される. 一致性・有効性はないが, そもそも全く違う値に収束する最小二乗法にくらべれば妥当な選択である.

さらに, この2段階最小二乗法のバイアスを軽減した方法として, ジャックナイフ法を応用した Jackkife IV推定量 (JIVE) がある (これも [GMM] 一般化モーメント法と操作変数 - ill-identified diary で言及している).

加えて, モデルを操作変数を含めた多変量回帰モデルとみなして最尤推定する, 制限情報最尤法 (LIML) というのもある ([GMM] 非線形モデルでの一般化モーメント法と操作変数 - ill-identified diary). LIML は, サンプルサイズが大きくなると2段階最小二乗法に漸近的に一致するが, サンプルサイズの小さいうちは, 2段階最小二乗法より分散が小さい傾向があると言われている. そこで, LIML も比較対象にした.

コードと結果

2段階最小二乗法は, 計量経済学でよく使う手法をあつめた AER パッケージで提供されている ivreg() を使う. 一方, JIVE と LIML を一発で推定してくれる関数は存在しない*1ので, 自分で作成する必要がある. そこで, 方針の簡単な説明をする.

LIML についてだが, 尤度に正規分布をあてはめた基本的な最尤法の一種なので, 非線形最適化問題を解く nlm() 関数に尤度関数とデータを与えるだけでいい*2が, 前回掲載した尤度関数をそのまま nlm() に与えても計算できない. そこで, Hayashi (2000, Econometrics) の Chapter 8 にあるように, まず共分散行列について最適化問題を解き, それを尤度関数に代入することで, 共分散行列を消して未知数が係数パラメータだけの尤度関数

\begin{align} \ln\mathcal{L}(\bar{\boldsymbol{\Gamma}},\bar{\mathbf{B}})= & -\frac{1+L}{2}\ln2\pi-\frac{1+L}{2} \\ &- \frac{1}{2}\ln\left|\frac{1}{N}\sum_{i}(\bar{\boldsymbol{\Gamma}}\boldsymbol{y}_{t}+\bar{\mathbf{B}}\boldsymbol{x}_{t})(\bar{\boldsymbol{\Gamma}}\boldsymbol{y}_{t}+\bar{\mathbf{B}}\boldsymbol{x}_{t})^{\prime}\right|\\ = & -\frac{2}{2}\ln2\pi-\frac{L+1}{2}\\ & -\frac{1}{2}\ln\left|\frac{1}{N}\sum_{i}\begin{bmatrix}y_{i}-\alpha-\beta x_{i}\\ x_{i}-\gamma-\delta x_{i} \end{bmatrix}\begin{bmatrix}y_{i}-\alpha-\beta x_{i}\\ x_{i}-\gamma-\delta x_{i} \end{bmatrix}^{\prime}\right|\end{align}

にすることで解く*3. 各種検定量や標準誤差を求めるには共分散行列も続けて計算する必要があるが, 今回は省いた.

もう1点は, JIVE についてで, これは誘導方程式

\begin{align} x_{i}= & \gamma+\delta z_{i}+u_{i}\end{align}

について, j 番目のオブザベーションを除いた N-1 個のサンプル で 予測値 \tilde{x}_{j} を計算するためのパラメータ \tilde{\gamma}_{j} , \tilde{\delta}_{j} を求める, というのを N 回繰り返す. よって, 他の推定方法と比べてかなり時間がかかる. さらに, JIVE は, 最終的に

\begin{align} \tilde{\boldsymbol{\beta}}_\mathit{JIV}:= & \left[\tilde{\mathbf{X}}^{\prime}\mathbf{X}\right]^{-1}\tilde{\mathbf{X}}^{\prime}\boldsymbol{y}\end{align}

という形で求めるので, \tilde{\mathbf{X}} を求めたら後は lm() で簡単に, というふうにはできない. そこで, 線型方程式を解く solve() 関数で,

\begin{align} \left[\tilde{\mathbf{X}}^{\prime}\mathbf{X}\right]\tilde{\boldsymbol{\beta}}_{\mathit{JIV}}= & \tilde{\mathbf{X}}^{\prime}\boldsymbol{y}\end{align}

を解いて係数を求めることになる.

なお, JIVE には

\begin{align} \tilde{\boldsymbol{\beta}}_\mathit{JIV2}:= & \left[\tilde{\mathbf{X}}^{\prime}\tilde{\mathbf{X}}\right]^{-1}\tilde{\mathbf{X}}^{\prime}\boldsymbol{y}\end{align}

の別バージョンが存在する( split-sample 推定量と呼ばれる (Cameron & Trivedi, 2005, Microeconometrics: Methods and Applications)). そこで,今回はそれぞれを JIVE1, JIVE2 と呼び, 両方計算する. JIVE2 は \tilde{\mathbf{X}} さえ求めたら後は lm() でよい.

# 本体 ver. 3.2.0
library(ggplot2)  # ver. 1.0.1
library(ggthemes) # ver. 2.1.2 デフォルトのカラーパレットが毒々しすぎるので
library(reshape2) # ver. 1.4.1  データフレーム加工用
library(MASS)     # ver. 7.3-39 多変量乱数の作成・密度計算に必要
library(AER)      # ver. 1.2-3 操作変数法に必要
library(compiler) # ver. 3.2.0 計算を手軽にちょっと早くする

size     <- 10^3 # 最大サンプルサイズ
size.min <- 3    # 最小値
ser      <- 10   # 系列の数
x.mean   <- 2    # X の平均
x.sigma  <- 2    # X の分散
e.sigma  <- 2    # 誤差項の分散
z.mean  <- 0     # Zの平均
z.sigma  <- 2    # Zの分散
rho      <- 1    # 誤差項との共分散
kappa    <- 1.5  # 操作変数とXの共分散
Sigma    <- matrix(c(x.sigma, rho, kappa,
                     rho, e.sigma, 0,
                     kappa, 0, z.sigma), nrow=3 )
alpha    <- 1    # 切片
beta     <- 1.5  # 係数

# グラフ描画用関数
# type に指定した推定量だけ表示する
# width で beta を中心に表示する縦軸の幅を指定できる
ggLLN <- function(data, width=3, type=NULL, y.center=beta, x.max=size){
  if (is.null(type) ) gg <- ggplot(data)
  else gg <- ggplot(data[data$type %in% type,])
  gg + geom_path(aes(x=N, y=value, group=variable, linetype=series, color=type), size=.7) + scale_linetype_discrete(guide=F) + 
    
    geom_hline(yintercept = beta, linetype="dashed", color=5, size=1.2) +
    scale_x_log10() + coord_cartesian(xlim=c(3,x.max), ylim=c(y.center - width/2, y.center + width/2)) +
    labs(x="N (対数)", y=expression(beta) ) + 
    theme(axis.title =element_text(size=20), 
          axis.title.y =element_text(angle = 0),
          legend.title=element_blank(),
          legend.text =element_text(size=15)) +
    scale_color_colorblind()
}

# LIML 用の尤度関数作成
# 他の計算方法もあるが, せっかくなので素朴に最尤法で解く
nlnL <- function(pars, data){
  # pars = alpha beta gamma delta
  # y = alpha + beta * x  + error1
  # x = gamma + delta * z + error2
  alpha <- pars[1]; beta <- pars[2]; gamma <- pars[3]; delta <- pars[4]
  N     <- nrow(data)
  M     <- 2
  Gamma <- matrix(c(1, 0, -beta, 1), nrow=2)
  Beta  <- matrix(c(-alpha, -gamma, 0, -delta), nrow=2)
  Y     <- t(data[,c("y","x")])
  Z     <- t(cbind(1,data$z))
  con.L <- nrow(data)*log(2*pi)/2 + log(det( (Gamma %*% Y + Beta %*% Z) %*% t(Gamma %*% Y + Beta %*% Z) )/nrow(data) )/2 + M/2
}
# nlm(f = nlnL, p=c(a0, b0, g0, d0), data=df ) のように使う

# jackknife IVE 推定用の関数 (単回帰 just-identified の場合のみ)
# reduced に誘導方程式を書く
jive.reg <- cmpfun(function(formula, reduced, data){
  # 時間がかかるので cmpfun で高速化する
  Xtilde <- matrix(nrow=nrow(data), ncol=2)
  Xtilde[,1] <- 1
  for(i in 1:nrow(data) ){
    # Xtilde[i,2] <- lm(formula = reduced, data = data)$coefficients %*% c(1, data$z[i])
    Xtilde[i,2] <- lm(formula = reduced, data = data[-i,])$coefficients %*% c(1, data$z[i])
  }
  
  # JIVE1: 線形方程式の形にして解く
  Xtilde2 <- t(Xtilde) %*% matrix(data = c(rep(1,nrow(data) ), data$x), ncol=2 )
  Ytilde  <- t(Xtilde) %*% data[,as.character(formula[[2]])]
  res1 <- res <- solve(a = Xtilde2, b = Ytilde)[2,1]
  
  # JIVE2: X を両方 predict にしたバージョン
  df.jive <- data
  df.jive[,as.character(formula[[3]])] <- Xtilde[,2]
  if (sum(is.na(Xtilde[,2]) ) == 0 ){ # 1段階目の結果が NA だとエラーになるので
    res2 <- lm(formula = formula, data=df.jive)$coefficients[2]
  } else {
    res2 <- NA
  }
  return(list(res1, res2))
}
)

# 擬似データ作成
set.seed(1)
Xe   <- mvrnorm(n = size*ser, mu = c(x.mean, 0, z.sigma), Sigma = Sigma)
y    <- alpha + beta*Xe[,1] + Xe[,2]
w    <- cbind(y,Xe)
colnames(w) <- c("y", "x","e", "z")
df <- data.frame(N=rep(1:size,ser), w)
df$e <- NULL # 誤差項は未知なので消す

# OLS, 2SLS, LIML, JIVE の結果格納用行列
res.ols   <- matrix(nrow=size, ncol = ser)
res.2sls  <- matrix(nrow=size, ncol = ser)
res.liml  <- matrix(nrow=size, ncol = ser)
res.jackk1 <- matrix(nrow=size, ncol = ser)
res.jackk2 <- matrix(nrow=size, ncol = ser)

system.time({
  for (i in 1:ser){
    for(j in size.min:size){
      print (paste("series:", i, ",", "iter:", j) )
      df.temp <- df[seq(from =size*(i-1)+1, to = size*(i-1)+j),c("y","x","z")]
      # OLS
      res.ols[j,i] <- lm(formula = y~x, 
                         data=df.temp)$coefficients[2]
      # 2SLS
      res.2sls[j,i] <- ivreg(formula = y~x|z,
                             data = df.temp)$coefficients[2]
      #  LIML
      res.liml[j,i]  <- nlm(f = nlnL, p=c(1, 1.4, .5, 0.5), data=df.temp)[[2]][2] # 初期値は適当
      
      # jackknife iv
      res <-  jive.reg(formula = y~x, reduced = x~z, data=df.temp)
      res.jackk1[j,i] <- res[[1]]
      res.jackk2[j,i] <- res[[2]]
    }
  }
})

colnames(res.ols) <- paste("ols", 1:ser, sep="")
colnames(res.2sls)  <- paste("2sls", 1:ser,sep="")
colnames(res.jackk1) <- paste("JIVEi", 1:ser, sep="")
colnames(res.jackk2) <- paste("JIVEii", 1:ser, sep="")
colnames(res.liml) <- paste("LIML", 1:ser, sep="")

res.all <- cbind(res.ols, res.2sls, res.jackk1, res.jackk2, res.liml)
res.all <- data.frame(N =  1:size, res.all)
res.melt <- melt(res.all, measure.vars = colnames(res.all)[-1])

res.melt$type <- "OLS"
res.melt$type[grep("2sls", res.melt$variable)] <- "2SLS"
res.melt$type[grep("JIVEi", res.melt$variable)] <- "JIVE1"
res.melt$type[grep("JIVEii", res.melt$variable)] <- "JIVE2"
res.melt$type[grep("LIML", res.melt$variable)] <- "LIML"
res.melt$series <- sub(x= res.melt$variable, pattern = ".+([0-9]+)$", replacement= "\\1")

ggLLN(res.melt, width = 2, type=c("OLS", "2SLS","LIML"))
ggLLN(res.melt, width = 2, type=c("LIML", "JIVE1","JIVE2"))
ggLLN(res.melt, width = 2, type=c("2SLS", "JIVE1","JIVE2"))


図1: OLS と 2SLS

f:id:ill-identified:20150511194955p:plain

実行する場合, JIVE の推定のせいで2~3時間くらいかかるので注意*4. グラフを描画するあたりで警告メッセージが出るが, これはサンプルサイズが 1とか2とかのときに計算できずに欠損値を返しているのが原因なので, 気にしなくて良い.

図1 を見ると, 理論通り OLS は操作変数を用いた他の全ての推定量とは違う値に収束している. 確かに OLS は収束がきれいで誤差が小さいようだが, そもそも違う値に収束するのでは意味がない. 一方で, 2SLS と LIML は真の値である 1.5 に収束している (LIML は漸近的に 2SLS に近づくのだが, 今回のシミュレーションでは2SLSとLIML がほとんど完全に重なってしまった. 乱数をきれいな正規分布にしたからか?). では, 次に 2SLS とJIVE を比較してみよう.


図2: 2SLS と JIVE

f:id:ill-identified:20150511195036p:plain

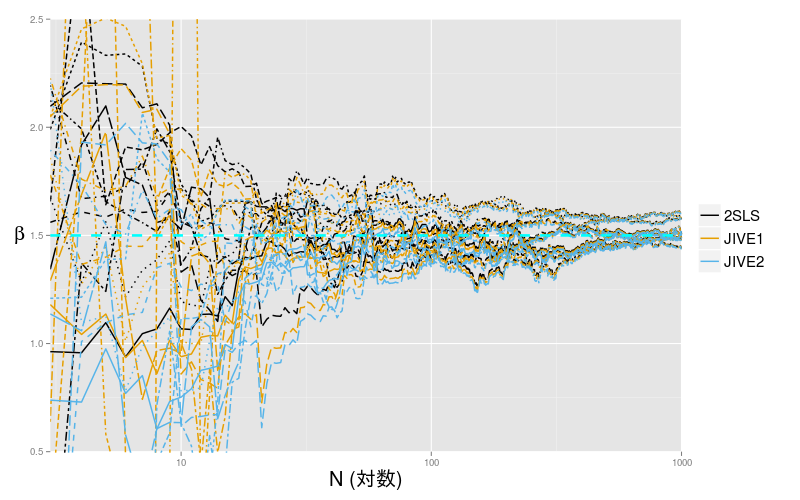
図2 ではサンプルサイズ 1000 以上では 2SLS と JIVE1, 2 の差は見られなくなるが, それより小さい時には JIVE1, 2 いずれも 2SLS よりだいぶばらつきが多いという結果になった. バイアスが減るとは言うが, 今回の例では分散の大きさのほうが気になる. バイアスがゼロ方向になるか, OLS 方向になるか, という違いがあるので, サンプルサイズがどうしても十分に得られないような限定的な状況でのみ, 使えるのだろう. R のパッケージでも実装しているものがないというのは, 使える機会が少ないからだろうか.

ところで, 操作変数法には1つ注意点があって, それは操作変数の相関が小さいと誤差が大きくなるというものである (弱相関操作変数の問題). そこで, すこし極端だが, 操作変数の相関パラメータ kappa を 1.5 から 0.2 に変えてもう一度同じシミュレーションをしてみる.


図3 弱相関操作変数

f:id:ill-identified:20150511195115p:plain

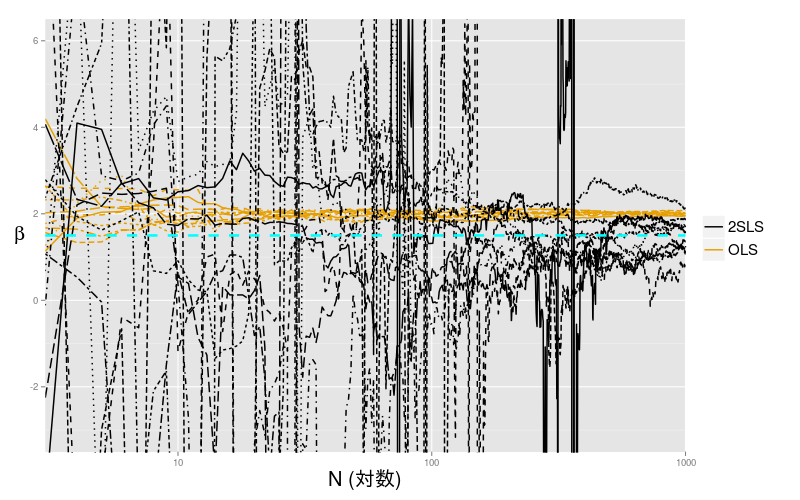
図3 を見ると 2SLS の線が跳ねまわっているが, このように弱相関操作変数を使うと (これは極端な例だが) 非常に不安定になる. たしかにOLS は一致推定量ではないが, 2SLS がここまで不安定ならば, むしろ2SLSの推定量を選ぶことで不確実さが増す. OLS の真の値とのずれは, 誤差項と説明変数の相関の大きさで決まるので, 誤差項と説明変数の相関と 操作変数と説明変数の相関のいずれも弱いような状況ならば, むしろ真の値とのずれを諦めて OLS を選択するという手もなくはない. そもそも操作変数がうまく機能しているか (識別されているか) を断定する方法はないので, 実用上はいずれにせよ, OLS と操作変数を用いた推定量を両方計算して比較することが多い.


参考文献

Cameron, A. C., & Trivedi, P. K. (2005). Microeconometrics: Methods and Applications. Cambridge University Press.

Hayashi, F. (2000). Econometrics. Princeton University Press.

*1:LIML は, 共分散構造分析をする SEM パッケージで利用可能だが, 構文が複雑なので今回は使わなかった

*2:ただし, nlm() は最小化問題を解くので, 通常の尤度関数と符号を逆にしなければならない.

*3:このような尤度関数を concentrated (集約?) 尤度関数と呼ぶ.

*4:JIVE の計算箇所だけコメントアウトすればかなり短くなる

ill-identified 読者になる

広告を非表示にする
コメントを書く