概要

讃岐富士とも呼ばれる*1 飯野山の形状が正規分布っぽいという説について, 本当にそうなのか, 標高データを非線形最小二乗法であてはめることで科学的に検証した.

はじめに

近年, 以下のツイートが話題を呼んでいる.

ぐぐってみると, 飯野山が正規分布ではないか, と考える人間は以前からいるようである. 正規分布ならばパラメータを持つが, 少し調べた限りでは, 飯野山のパラメータに関する研究は著者不明の pdf のみであり, 適当に切り出した画像に対して eye-fitting, つまり目分量で曲線を当てはめ, $y=k/(1+\alpha x^2)$ の双曲関数の当てはまりが良いとしたものである.

飯野山に限定しないならば, 富士山の画像に対して確率密度関数を当てはめた『富士山が美しすぎたので、フィッティングをしてしまいました... - プロクラシスト』が存在する. しかしこちらの当てはまりの評価もまた目分量で合わせただけである*2.

一方, 理論モデルとしては粒状体が滑り出さない最大角を意味する安息角という概念があり, 様々な事例に対して実験による安息角の検証が行われているようだが, 山の曲線を表現できる理論モデルまでは発展していないようだ.

幸いなことに, 国土地理院のサイトから標高データをダウンロードすることができる. そこで確率分布として見た場合の飯野山のパラメータを, 非線形最小二乗法で当てはめ, パラメータの推定と当てはまりの評価をしてみる. (2019/8/26: 先行研究のサーベイを追加.)

方法

標高データはランダムサンプリングではなく, グリッド状に等間隔にサンプリングされたものなので, 最尤法で当てはめることはできない. また, 以前『[R] 東京都の所得階級分布から元の分布を推定する方法 - ill-identified diary』で書いたようなヒストグラムから元の分布をパラメトリックに推定する, という方法を2次元分布に拡張すれば応用できそうに一見思えるが, z軸の情報が頻度ではないので不可能である. そこで, 密度関数を非線形最小二乗法で当てはめる方法を考える. つまり, 経度を $x$ , 緯度を $y$ , 標高 $z$ の観測点が $N$ 個存在するとして,

$\begin{aligned} \min\sum_{i=1}^{N}&\left(z_{i}-\kappa p(x_{i},y_{i}\mid\cdots)\right)^{2} \end{aligned}$

を満たすようなパラメータを選ぶ. 標高は確率として正規化されていないため, 密度関数に乗数パラメータ $\kappa$ を乗じている. よってこの方法では, 標高のスケールが変動するため「視覚的に正規分布っぽい」ということとは必ずしも一致しない*3ことに注意する.

当てはめる密度関数は2変量正規分布である.

パラメータが,

$\begin{align} \boldsymbol{\mu}:=\begin{bmatrix}\mu_{X}\\ \mu_{Y} \end{bmatrix}, & \boldsymbol{\Sigma}:=\begin{bmatrix}\sigma_{X}^{2} & \rho\sigma_{X}\sigma_{Y}\\ \rho\sigma_{X}\sigma_{Y} & \sigma_{Y}^{2} \end{bmatrix}\end{align}$

である2変量正規分布の同時密度関数は,

$\begin{align} p_{\mathcal{N}}(x,y\mid\cdots):= & \frac{1}{2\pi\sigma_{X}\sigma_{Y}\sqrt{1-\rho^{2}}}\\ & \exp\left[-\frac{1}{2(1-\rho^{2})}\left(\frac{(x-\mu_{X})^{2}}{\sigma_{X}^{2}}+\frac{(y-\mu_{Y})^{2}}{\sigma_{Y}^{2}}-\frac{2\rho(x-\mu_{X})(y-\mu_{Y})}{\sigma_{X}\sigma_{Y}}\right)\right] \end{align}$

と書ける (たいていの統計学の教科書には書いてあるので説明略).

しかし, 正規分布に似た形状の分布は他にもある. そこで, 2変量 t 分布と, 2変量ロジスティック分布についても当てはめてみる.

多変量 t 分布は, 例えばKotz & Nadarajah (2004), Shaw & Lee (2008) で与えられている. 2変量正規分布に合わせて書くならば, 自由度 $v$ , 位置・尺度パラメータ $\mu_{X},\mu_{Y},\sigma_{X},\sigma_{Y},\rho$ に対して,2変量 t 分布の同時密度関数は以下のようになる.

$\begin{align}p_{\mathit{student}}(x,y\mid\cdots):= & \frac{\Gamma( (v+2)/2)}{\Gamma(v/2)v\pi\sigma_{X}\sigma_{Y}\sqrt{1-\rho^{2}}}\\ & \left[1+\frac{1}{2v(1-\rho^{2})}\left(\frac{(x-\mu_{X})^{2}}{\sigma_{X}^{2}}+\frac{(y-\mu_{Y})^{2}}{\sigma_{Y}^{2}}-\frac{2\rho(x-\mu_{X})(y-\mu_{Y})}{\sigma_{X}\sigma_{Y}}\right)\right]^{-(v+2)/2} \end{align}$

今回は, 自由度 $v=1$ のとき, つまり2変量コーシー (Cauchy) 分布と, 自由度5の場合でのみ計算した.

多変量のロジスティック分布はあまり馴染みがないが, Gumbel (1961), Malik & Abraham (1973) で紹介されている標準多変量ロジスティック分布を参考にすると, 位置・尺度パラメータを加えた2変量の場合は,

$\begin{align} p_{\mathit{logis}}(x,y\mid\cdots):= & \frac{2\exp\left[-\left(\frac{x-\mu_{X}}{\sigma_{X}}+\frac{y-\mu_{Y}}{\sigma_{Y}}\right)\right]}{\sigma_{X}\sigma_{Y}\left[1+\exp\left(-\frac{x-\mu_{X}}{\sigma_{X}}\right)+\exp\left(-\frac{y-\mu_{Y}}{\sigma_{Y}}\right)\right]^{3}}\end{align}$

となる (アフィン変換とヤコビアンからすぐに求められる. 多変量分布の導出については竹村 (1991), Casella & Berger (2002) など統計学の標準的な教科書を参考に.). しかしこの定義では $X,Y$ の相関のある場合が考慮されていない. 相関パラメータを考慮すると, このタイプの分布は非常に複雑になる (簡単にできる方法を知っている人は教えてほしい) ためだ.

しかし, 実際にこれらの関数を当てはめ, 実測値とモデル値の誤差をプロットをしてみると, 正規分布, コーシー分布でいずれも頂上付近の誤差が大きくマイナスになっている (図1). 残差がマイナスということは予測値が過大であるということなので, これらの分布と比べて飯野山は頂点付近が平坦な形状の分布なのではないか, と考えられる.

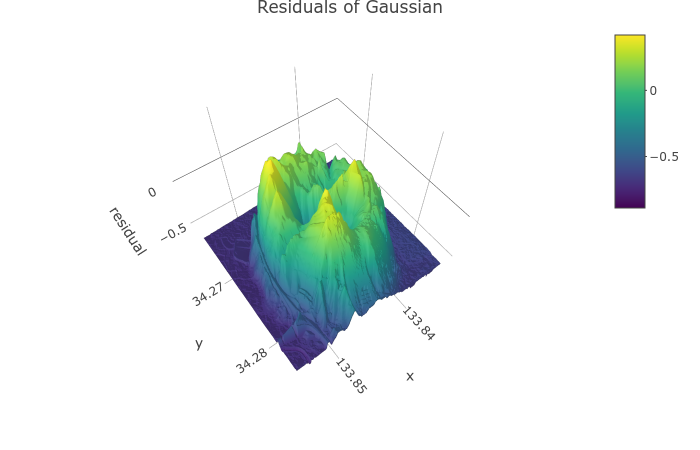
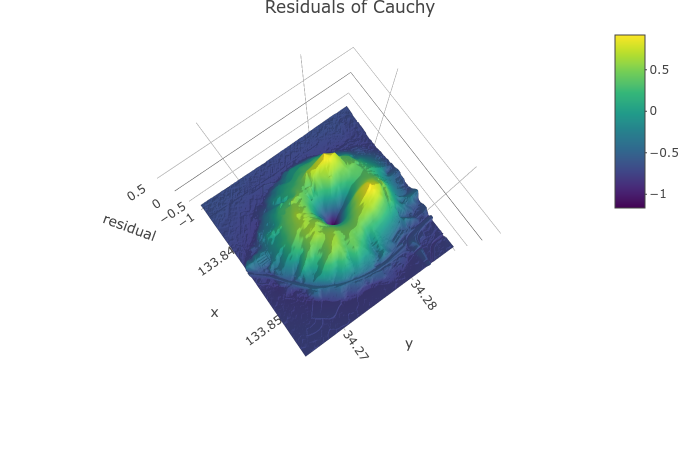
図1: (左) 正規分布に対する残差プロット, (右) コーシー分布に対する残差プロット

以下のページではピーク付近が平坦な分布がいくつか挙げられている.

Is there a plateau-shaped distribution? - Cross Validated

しかし, Subbotin (1923) のようないわゆる一般化正規分布をはじめ, 多くは関数が滑らかでないため非線形最小二乗法では計算できないので面倒である. そこで, この中でも非線形最小二乗法が適用可能な Is there a plateau-shaped distribution? - Cross Validated で提案されている関数を利用する. 以下, 参考ページのタイトルにならいこれを台地分布 (plateau distribution) と呼ぶ. パラメータは非負の $\alpha$ のみである.

$\begin{align} p_{P}(x\mid\alpha):= & \frac{\alpha}{\pi}\sin\left(\frac{\pi}{2\alpha}\right)\frac{1}{1+x^{2\alpha}} \end{align}$

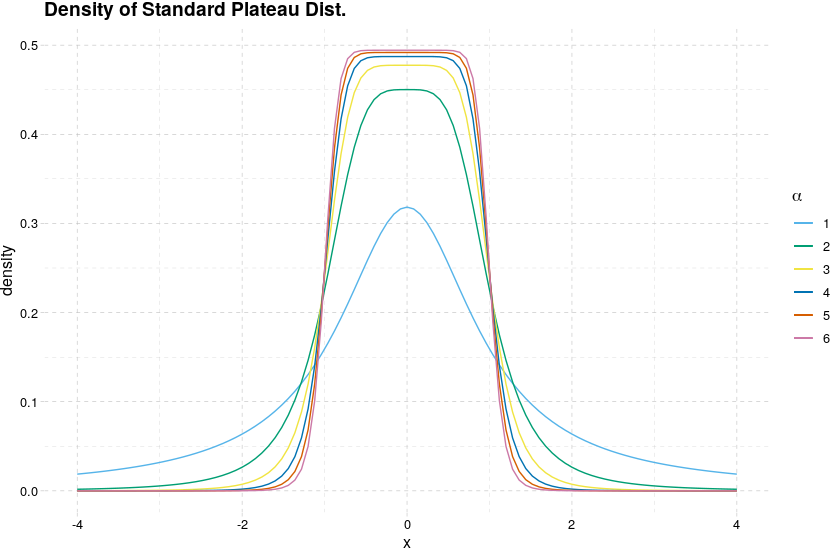
この分布は $\alpha$ が大きくなるほど一様分布 $U(-1,1)$ に近づく (図2).

この分布に位置パラメータと尺度パラメータを追加すると,

$\begin{align} p_{P}(x\mid\cdots):= & \frac{\alpha}{\pi\sigma}\sin\left(\frac{\pi}{2\alpha}\right)\frac{1}{1+\left(\frac{x-\mu}{\sigma}\right)^{2\alpha}} \end{align}$

となり, 正規分布やロジスティック分布の場合と同様に, 2変量に拡張するとその同時密度関数は,

$\begin{align} p_{P}(x,y\mid\cdots)= & \frac{\alpha^{2}\sin^{2}(\pi/2\alpha)}{\pi^{2}\sigma_{X}\sigma_{Y}}\left\{ \left(1+\left(\frac{x-\mu_{X}}{\sigma_{X}}\right)^{2\alpha}\right)\left(1+\left(\frac{y-\mu_{Y}}{\sigma_{Y}}\right)^{2\alpha}\right)\right\} ^{-1} \end{align}$

となる. こちらも相関係数を考慮すると複雑になりすぎるので, 相関のない分布を当てはめる. この分布は, $\alpha=1$ のとき, 先行研究1 でよく当てはまると評された曲線と同型になる. そこで今回は $\alpha=1$ と, 頂点付近がより平坦になる $\alpha=2$ の場合を考える (図3).

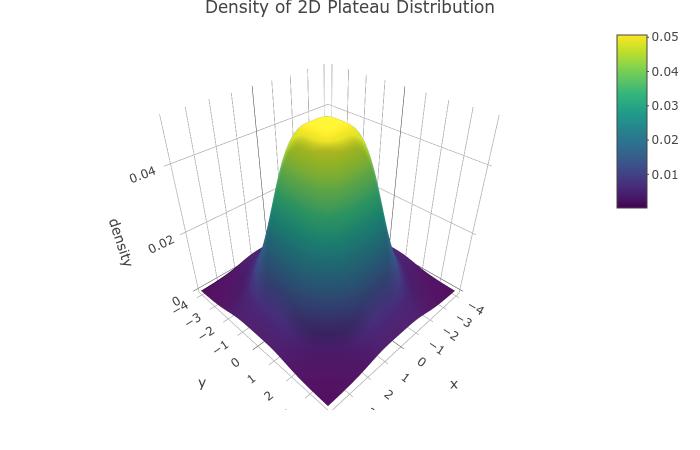
実際の処理

標高データは国土地理院の基盤地図情報ダウンロードサービスから取得した. 現時点では, ユーザー登録さえすれば誰でも情報にアクセスできる.

基盤地図情報ダウンロードサービス

飯野山が含まれるメッシュ番号は 513336 であり, この区画の数値標高モデルを取得した. 数値標高モデルは測量結果を5m/10mのメッシュ単位で整形したデータである*4.

ダウンロードした DEM データを R に読み込む方法は, 既に以下のサイトで紹介されていた.

国土地理院の数値標高モデルデータをラスタとしてRで扱う - cucumber flesh

このデータの構造はよくわからないのだが, いくつものファイルに分かれていてどこに何が含まれているのかよくわからないが, FG-GML-5133-36.+DEM5.+.xml でマッチする xml ファイルを片っ端から読み込めばいいらしい*5. ただし, 36A と 36B とあるファイルで, 座標が重複するため, 座標で一意になるように平均を取ることにした. このデータから等高線をプロットしたものが図 4である.

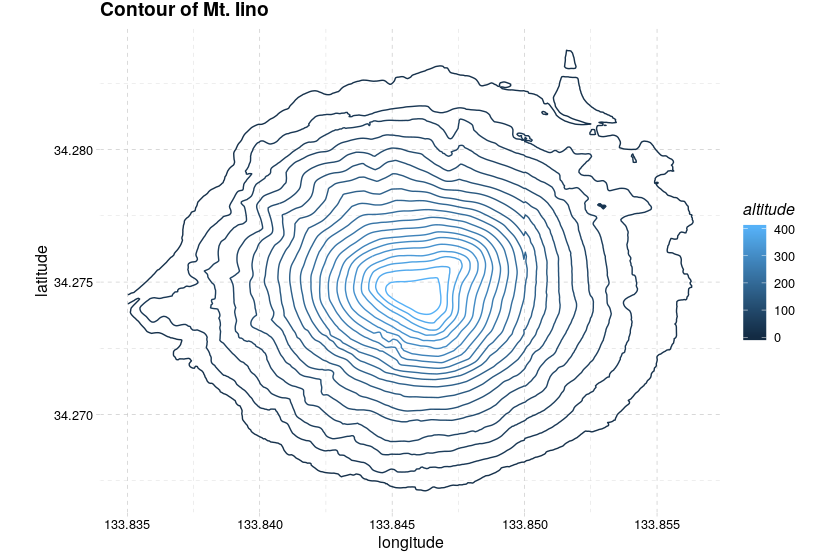
密度関数の形状は複雑で, また変数ごとにスケールも違うため, そのまま計算すると不安定となる. そのため, x, y, z 軸全てを標準化した上で計算した. よって, 計算結果をアフィン変換したものがパラメータの推定値になる.

一応解説しておく. 生データを $\boldsymbol{u}\in\mathbb{R}^{2}$ とすると, 今回密度関数に当てはめた $\boldsymbol{v}$ は,

$\begin{align} \boldsymbol{v}:= & \mathbf{B}^{-1/2}(\boldsymbol{u}-\boldsymbol{a})\end{align}$

で与えられている. $\boldsymbol{a},\mathbf{B}$ はそれぞれ生データの(標本) 平均と, 標準偏差を成分とする対角行列である:

$\begin{align} \boldsymbol{a}:=\begin{bmatrix}a_{X}\\ a_{Y} \end{bmatrix}, & \mathbf{B}:=\begin{bmatrix}b_{X}^{2} & 0\\ 0 & b_{Y}^{2} \end{bmatrix}\end{align}$

ここで, 正規分布や t 分布で現れる変数の2次形式部分は,

$\begin{align} (\boldsymbol{v}-\boldsymbol{\mu})^{\intercal}\boldsymbol{\Sigma}^{-1}(\boldsymbol{v}-\boldsymbol{\mu})= & (\mathbf{B}^{-1/2}(\boldsymbol{u}-\boldsymbol{a})-\boldsymbol{\mu})^{\intercal}\boldsymbol{\Sigma}^{-1}(\mathbf{B}^{-1/2}(\boldsymbol{u}-\boldsymbol{a})-\boldsymbol{\mu})\\ = & (\boldsymbol{u}-\boldsymbol{a}-\mathbf{B}^{1/2}\boldsymbol{\mu})^{\prime}\mathbf{B}^{-1/2}\boldsymbol{\Sigma}^{-1}\mathbf{B}^{-1/2}(\boldsymbol{u}-\boldsymbol{a}-\mathbf{B}^{1/2}\boldsymbol{\mu})\\ = & (\boldsymbol{u}-(\boldsymbol{a}+\mathbf{B}^{1/2}\boldsymbol{\mu}))^{\prime}\mathbf{B}^{-1}\boldsymbol{\Sigma}^{-1}(\boldsymbol{u}-(\boldsymbol{a}+\mathbf{B}^{1/2}\boldsymbol{\mu}))\end{align}$

と表せる. さらに, ヤコビアンは,

$\begin{align} \left|\mathbf{J}(\boldsymbol{v},\boldsymbol{u})\right|= & \left|\mathbf{B}^{-1}\right|=\frac{1}{b_{X}b_{Y}}\end{align}$

であることから, $\boldsymbol{u}$ の位置・尺度パラメータ $\boldsymbol{m},\mathbf{S}$ は,

$\begin{align} \boldsymbol{m}= & \boldsymbol{a}+\mathbf{B}\boldsymbol{\mu}=\begin{bmatrix}a_{X}+\sigma_{X}\mu_{X}\\ a_{Y}+\sigma_{Y}\mu_{Y} \end{bmatrix},\\ \mathbf{S}= & \mathbf{B}\boldsymbol{\Sigma}=\begin{bmatrix}b_{X}^{2}\sigma_{X}^{2} & \rho b_{X}\sigma_{X}b_{Y}\sigma_{Y}\\ \rho b_{X}\sigma_{X}b_{Y}\sigma_{Y} & b_{Y}^{2}\sigma_{Y}^{2} \end{bmatrix}\end{align}$

と表現できる. 一方で, ロジスティック分布と台地分布は積が存在しないが, 共分散も存在しないので単変量で個別に計算すれば,

$\begin{align} \boldsymbol{m}=\begin{bmatrix}a_{X}+\sigma_{X}\mu_{X}\\ a_{Y}+\sigma_{Y}\mu_{Y} \end{bmatrix}, & \mathbf{S}=\begin{bmatrix}b_{X}^{2}\sigma_{X}^{2} & 0\\ 0 & b_{Y}^{2}\sigma_{Y}^{2} \end{bmatrix}\end{align}$

となることがわかる.

プログラムは以下で公開している.

gist99c556d70f4cb99c40fb1e46a4077c28

結果と結論

パラメータの推定結果は表1のとおりである.

表1: 推定したパラメータ
name	$\kappa$	$\mu_x$	$\mu_y$	$\rho$	$\sigma_x$	$\sigma_y$
Cauchy	12.2513	133.8459	34.2747	-0.0221	0.0042	0.0033
Gaussian	4.4604	133.8459	34.2748	-0.0298	0.0028	0.0023
logistic	51.4076	133.8458	34.2747		0.0018	0.0014
plateau (1)	3.1101	133.8459	34.2748		0.0024	0.0019
plateau (2)	4.5275	133.8459	34.2748		0.0035	0.0028
Student (5)	230.3652	133.8459	34.2748	-0.0250	0.0192	0.0153

どのモデルがより当てはまっているかは, 実測値とモデル値の平均二乗誤差根 (RMSE) がより小さいかで判断した. RMSE は以下で定義される. 参考に, 平均絶対誤差 (MAE) もあわせて表2に掲載した.

$\begin{align} \mathit{RMSE}:= & \sqrt{N^{-1}\sum_{i=1}^{N}(y_{i}-\hat{y}_{i})^{2}}\end{align}$

表2 のように, モデルの候補の中では, 正規分布の当てはまりが最も良いという結果になった. だが, 当初の「飯野山は正規分布であるか」という問いに対しては, 「思ったほど正規分布の形状には似ていない」ということが残差プロットからわかる. 頂上付近の残差が特に大きいためだ.

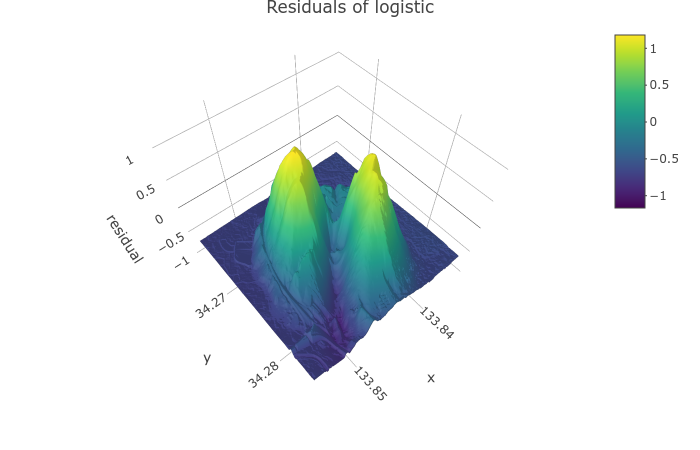
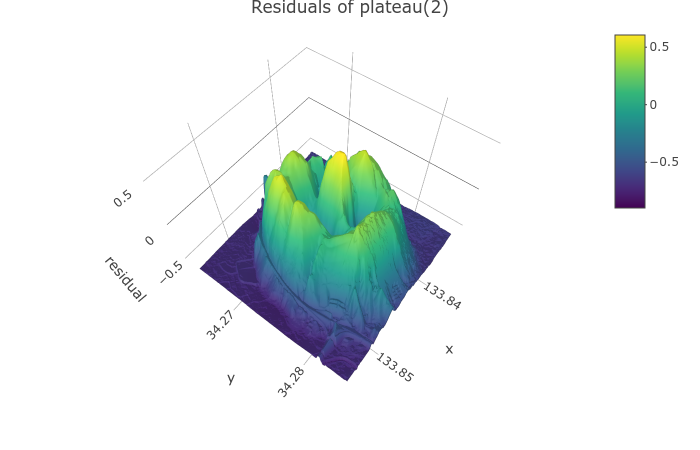
加えて, 2変量間の相関が見られることもわかる. 先行研究に反して $\alpha=1$ では台地分布の当てはまりが最も悪い一方で, $\alpha=2$ が正規分布の次に当てはまりが良いというのは興味深い. 正規分布や t分布など相関パラメータのある分布では, いずれも相関係数がある程度の大きさを持っているので, 相関のあるモデルのほうが当てはまりがよいなると考えられる. これはロジスティック分布に対する残差プロットの特徴的な形状からも裏付けられる (図5).

しかし, それでもなお台地分布の当てはまりが大きいということは, 頂点付近が平坦で, かつ相関のある2変量分布を作ることができればより当てはまりがよくなる可能性がある. 台地分布の台地部分は矩形に近づくため, 台地が楕円状になるようなものならより当てはまりが良くなるかもしれない (図6).

つまり, 相関係数の大きい2変量正規分布も正規分布ではあるが, 飯野山は実際には, 対称かつなめらかな「典型的な, 想像で思い描かれるような」曲線を描く正規分布とは, やや異なる形状をしていることがわかる.

表2: 当てはまりの結果
name	RMSE	MAE
Gaussian	0.4859	0.4191
plateau (2)	0.5040	0.4466
Student (5)	0.5175	0.4629
logistic	0.5672	0.5177
Cauchy	0.5850	0.5374
Plateau (1)	0.5866	0.5387

今回は, 飯野山がどのような分布に従うか, またそのパラメータが何かということを調べた. 一方で, 地学的な観点, つまり山の風化という物理現象の理論モデルを立てる, というところからアプローチすることでその分布形状を求めることもできるかもしれない. これは今後の課題である.

参考文献

著者不明 (2013) 『富士山の方程式 -自然は数理を模倣する-』URL: http://www10.plala.or.jp/mondai/columun/fuji.pdf
Casella, G., & Berger, G. L. (2002). Statistical inference. 2nd ed., Thomson Learning.
Gumbel, E. J. (1961). Bivariate Logistic Distributions. Journal of the American Statistical Association, 56(294), 335. doi:10.2307/2282259
Kotz, S., & Nadarajah, S. (2004). Multivariate t distributions and their applications. Cambridge ; New York: Cambridge University Press.
Malik, H. J., & Abraham, B. (1973). Multivariate Logistic Distributions. The Annals of Statistics, 1(3), 588–590. doi:10.1214/aos/1176342430
Shaw, W., & Lee, K. (2008). Bivariate Student t distributions with variable marginal degrees of freedom and independence. Journal of Multivariate Analysis, 99(6), 1276–1287. doi:10.1016/j.jmva.2007.08.006
Subbotin, M. F. (1923). On the Law of Frequency of Error. Matematicheskii Sbornik, 31(2), 296–301. Retrieved from http://mi.mathnet.ru/eng/msb6854
竹村彰通. (1991). 現代数理統計学. 創文社.