[QGIS] [R] QGIS と空間統計モデル (CARモデル)

概要・前置き

以前も何度か R で地図を作る方法を紹介していたが, 自分のプログラミングテクが雑なこともあり, 冗長なコードの掲載であまり便利でないのではという印象を持たれる恐れもあった. そこで, GUI で操作のできるわりに高機能な QGIS (Quantum GIS; QGISプロジェクトへようこそ!) の使い方についても紹介したいと考えていた.
すると先日, 岩波DSが発売され, CAR モデルが取り上げられていたので, これと絡めて書くことにした.
ただ, 実際は QGIS で直接 CAR の推定はできないので, 今回はあまり QGIS の出番はなく, 空間統計モデルの説明と R へのつなげ方がメインになってしまった…… 次回以降にデータハンドリングの場面での QGIS の強みを紹介したい……
分量は PDF 換算 6ページ.

空間計量経済モデル

主題である CAR ( Conditional AutoRegressive; 条件付き自己回帰) モデルに触れる前に, まず一般的な空間自己相関モデルについて話しておく. 株価などの金融時系列データならば, 過去の値を説明変数にして現在の値に当てはめ, 予測する時系列的な自己回帰モデルがよく使われる. つまり, $\{y_{1},\,y_{2},\,\cdots,\,y_{T}\}$ という時系列データがあって,

$\begin{align} y_{t}= & f(y_{t-j}),\,t=0,\,1,\,2,\,3,\, \cdots ,\, T \end{align}$

というような関係を意味する. 一方で, 自身の過去の値ではなく, 自身の周囲の周りの値によって, 自身の値を決定する「空間的な」自己回帰モデルというのもある. 時間以外のインデックス $i$ のついた $y_{1},\,\cdots,\,y_{i},\,\cdots,\,y_{N}$ があって, やはり

$\begin{align} y_{i}= & f(y_{j}),\,j\neq i\end{align}$

のように表される. 地理経済学の他にも, 伊東 (2015) の解説のように生態の調査でも用いられているようで, Lesage (1999) で挙げられている例も, ミシガン州のマイマイガの個体の分布である. マイマイガの幼虫は森林害虫であるため, 生態について昔から研究がなされているようだ. マイマイガの幼虫は, 飛ぶことはできないが風に吹かれることで移動する. つまり, まったくのランダムに自然に出現するのではなく, 最初にいた地点からわずかに近くに多く分布しやすい, という空間的な自己相関があると考えられる. ではこれを, 古典的な線形回帰モデルで表現できるだろうか?

空間統計モデリングでは空間的な関係を表す隣接行列 (contiguity or adjacency matrices) を得ることが重要になる. そこで, まずは簡単な例として, ミシガン州を9の区画に分けてマイマイガの個体数を調査したとする. 区画は碁盤の目のように分割され, 区画ごとに調査がなされたとしよう. 区画 $i$ の個体数を $y_{i}$ とする. 空間的な自己相関は, 隣接する区画にのみ作用し, 互いに隣接しない区画どうしでは相関がないものと仮定する*1. このとき, 全部で9区画の場合の中央の区画5は左右と上下の区画と隣接しているとみなせる. 他の区画も同様に上下左右と隣接しているので,以下のように各区画に順に番号を割り当てていくことで,

1	2	3
4	5	6
7	8	9

この各観測点ごとの隣接の情報を行列で表すことができる: 区画 $i$ が区画 $j$ に隣接しているとき, $(i,\,j)$ 成分が $1$ , 隣接していないならゼロとなる ( $i=j$ なら隣接ではないのでゼロ) ようにすると,

$\begin{align} \mathbf{W}= & \begin{bmatrix}0 & 1 & 0 & 1 & 0 & 0 & 0 & 0 & 0\\ 1 & 0 & 1 & 0 & 1 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 1 & 0 & 1 & 0 & 0 & 0\\ 1 & 0 & 0 & 0 & 1 & 0 & 0 & 1 & 0\\ 0 & 1 & 0 & 1 & 0 & 1 & 0 & 1 & 0\\ & & & & & \ddots\\ \\ \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 1 & 0 \end{bmatrix}\end{align}$

と表せる. 簡単のために碁盤の目状と言ったが, 都道府県や市区町村のようなより複雑な区域でも隣接行列を決定することはできる. また, 隣接の考え方にもいくつか種類があり, 上の例はチェスの駒にたとえて「ルーク型」である. 斜め方向を隣接というのなら「ビショップ型」, 上下左右と斜めを隣接していると定めるのなら「クイーン型」である. ただしどのタイプであれ, 定義から, $\mathbf{W}$ の対角成分は必ずゼロでなければならない. さらに, 重み付けに使う必要から, この $\mathbf{W}$ の各行の和が1になるように「標準化」する必要がある. よって, 上記のルーク型隣接行列は,

$\begin{align} \mathbf{W}= & \begin{bmatrix}0 & 1/2 & 0 & 1/2 & 0 & 0 & 0 & 0 & 0\\ 1/3 & 0 & 1/3 & 0 & 1/3 & 0 & 0 & 0 & 0\\ 0 & 1/3 & 0 & 1/3 & 0 & 1/3 & 0 & 0 & 0\\ 1/3 & 0 & 0 & 0 & 1/3 & 0 & 0 & 1/3 & 0\\ 0 & 1/4 & 0 & 1/4 & 0 & 1/4 & 0 & 1/4 & 0\\ & & & & & \ddots\\ \\ \\ \\ \end{bmatrix}\end{align}$

となる. この行列を掛けて,

$\begin{align} \begin{bmatrix}y_{1}\\ \vdots\\ y_{N} \end{bmatrix}= & \rho\mathbf{W}\begin{bmatrix}y_{1}\\ \vdots\\ y_{N} \end{bmatrix}+\begin{bmatrix}\varepsilon_{1}\\ \vdots\\ \varepsilon_{N} \end{bmatrix}\end{align}$

と表す. よって, $y_{i}^{\ast}=(\mathbf{W}\boldsymbol{y})_{i}$ とみなせば, $y_{i}^{\ast}$ は $y_{i}$ に隣接する区画での観測値の加重平均とみなせるので,

$\begin{align} y_{i}= & \rho y_{i}^{\ast}+\varepsilon_{i}\label{eq:far}\end{align}$

という通常の線形回帰モデルのようにあつかうことで, 隣接区画との自己相関パラメータ $\rho$ を推定できる1階の空間自己回帰 (FAR) モデル, あるいは時系列の類推から空間ラグモデルと呼ばれるものになる*2. これは定数項や他の説明変数を加えり, 誤差項にも自己相関を仮定したモデルへも拡張できて, それらは空間ダービン (Spatial Durbin) モデルとか, 空間自己回帰 (SAR) モデルとか呼ばれるものになる*3.

空間統計では, 単に自己相関といっても, 観測点どうしの距離が開くほど自己相関が減衰するという場合が多い. これは横軸に距離を, 縦軸を自己相関の大きさとしてプロットするとよくわかる. なお, このような距離と自己共分散の関係はバリオグラムという指標で表し, 空間統計でよく使われる*4. ここから, 隣接行列の代わりにより一般に, 成分に観測点どうしの距離に依存する関数を与えたウエイト行列を用いる場合があり, 地理的加重回帰 (GWR) モデルと呼ばれる.

ここまで紹介したモデルは, GWR モデルを除き, 古典的な計量経済学の枠組みでパラメータを適切に推定できる. また, R の spdep パッケージで実際の計算ができる. なお, Lesage (1999) には空間計量経済学のモデル全般について説明が書かれているが, CAR については言及されておらず, またサンプルコードが多く掲載されているものの全て matlab である.

CAR モデル

SAR モデル全般は, $\boldsymbol{\varepsilon}\sim\mathcal{N}(0,\,\sigma^{2}\mathbf{I}_{N})$ , というふうな正規分布か, さらに自己回帰項を合成して表されるという仮定だった. 一方で, CAR モデルの場合, さらに地点ごとに個別の誤差項を持つ分布であるとする. 言い換えると, 空間モデルに混合効果モデルを持ち込んだものとも言える. つまり, たとえば正規分布ならば, 分散共分散行列の対角成分以外にも非ゼロの成分が存在するため, 一般的な行列 $\mathbf{V}$ を用いて表される $\boldsymbol{\varepsilon}\sim\mathcal{N}(\mathbf{0},\,\sigma^{2}\mathbf{V})$ のような多変量正規分布となることを意味する. 伊東 (2015) などでは, CAR モデル, 特に intrinsic CAR, または Gaussian CAR と呼ばれるものの誤差項は

$\begin{align} \varepsilon_{i}|\varepsilon_{j\neq i}= & \mathcal{N}\left(\sum_{j}\frac{w_{i,j}\varepsilon_{j}}{\sum_{j}w_{i,j}},\,\frac{\sigma_{i}^{2}}{\sum_{j}w_{i,j}}\right)\end{align}$

というふうに表される (前後の記述と整合をとるため, 記号を変えている) が, そもそもこれはどういう意味かというのも書いておく. Besag, York, and Mollié (1991) では, 誤差項の事前分布を $\boldsymbol{\varepsilon}$ の同時分布として以下のように表している.

$\begin{align} p(\boldsymbol{\varepsilon}) & \propto\exp\left\{ -\sum_{i < j}w_{ij}\phi(\varepsilon_{i}-\varepsilon_{j})\right\} \end{align}$

$\phi(z)$ は任意の $|z|$ について増加する関数である. $w_{ij}$ は隣接行列の成分であるが, 先に紹介したものとは異なり, 隣接していれば 1, そうでなければゼロとなり, 列の和で除すことで標準化しない. 標準化しないのは最初の分布で表された完成形を見ての通りである. これは全ての $\{\varepsilon_{i}\}$ の同時分布だが, $\varepsilon_{i}$ 以外の残りの誤差項 $\varepsilon_{-i}$ に対する $\varepsilon_{i}$ の条件付き密度関数に書き換えると,

$\begin{align} p(\varepsilon_{i}|\varepsilon_{-i})\propto & \exp\left\{ -\sum_{j\in\delta_{i}}w_{ij}\phi(\varepsilon_{i}-\varepsilon_{j})\right\} \end{align}$

となる. ただし, このとき, $\delta_{i}$ は $i$ に隣接しているすべての地点という意味である.

さらに, $\phi$ を正数のパラメータ $\kappa$ を伴う $\phi(z)=z^{2}/2\kappa$ とおくと, 当初の正規分布の密度関数となる. これが intrinsic CAR である. 一方で, "intrinsic" でない CAR モデルとして, リモートセンシングなどでは $\phi(z)=|z|/\kappa$ がよく使われるらしい.

QGIS での操作

結論から言うと, 空間自己相関モデル全般を QGIS 単体で計算するのは難しい. しかし, 地理データのハンドリングに関しては QGIS は便利なので, モデルパラメータの推定の全段階までは QGIS でデータハンドリングを行い, それを R で読み込んで残りの工程を行う, という方針にする.

一番面倒なのは隣接行列の計算だろう. そこで, maps2WinBUGS というプラグインで WinBUGS フォーマットで隣接行列を出力し, R の CARBayes パッケージで CAR モデルを推定する, という予定だったのだが……, WinBUGS のグラフ機能用に地理データを変換する機能など, 今はあまり重要でない機能が多いので, 今回はこれを使わないことにした.

f:id:ill-identified:20151120002817p:plain

隣接行列の出力はできるが, R でやるよりも遅い……

QGIS で加工した地理データを R で読み込み, spdep と CARBayes で CAR モデルを推定することにする. WinBUGS は Windows 以外の OS での導入が面倒なので, より OS に依存しない CARBayes を利用することにした. もしも WinBUGS を利用したいというのなら, 伊東 (2015) を参考にすれば簡単にできるだろう. spdep は隣接行列を計算するのに必要である. 隣接行列を求めるだけなら rgeos パッケージでもいいが, spdep ならば SAR など他の空間自己相関モデルの推定ができるパッケージなのでこちらを採用した.

今回は例として, 国土数値情報ダウンロードサービスから東京都内の最新の公示地価データをダウンロードし, CAR モデルを適用してみた. 点データなので, ボロノイ分割してポリゴンに置き換える. 今回は, ボロノイポリゴンの隣接から隣接行列を求めることにした.

点データのレイヤを選択.
[ベクタ] -> [ジオメトリツール] -> [ボロノイポリゴン] を選択.
入力レイヤと出力ファイル名を選択し, バッファに 5% を指定して実行.

この処理は重いのでノート PC など, スペックが低いマシンを使っている場合は注意.

f:id:ill-identified:20151120001618p:plain

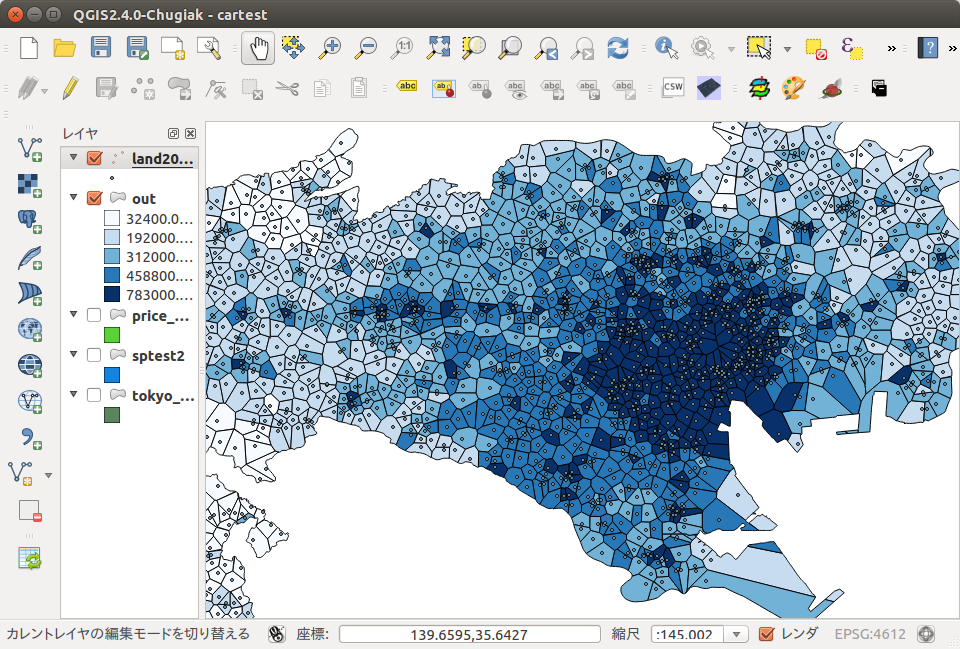
ポリゴン分割し単価で色分けした様子 (端は東京都の境界線でクリップしている)

2018/8/13: CARBayes を使った分析が色々とお粗末だったり GIS 関係のパッケージ事情が変わったりしたりしたので, 以降を大幅修正

出力されたポリゴンデータには, 変換前の点に対応した属性情報が紐付けられているので, これを R に読み込ませる.

まず, 地価の分布を確認する.

f:id:ill-identified:20180813004722p:plain — 地価の分布(対数)

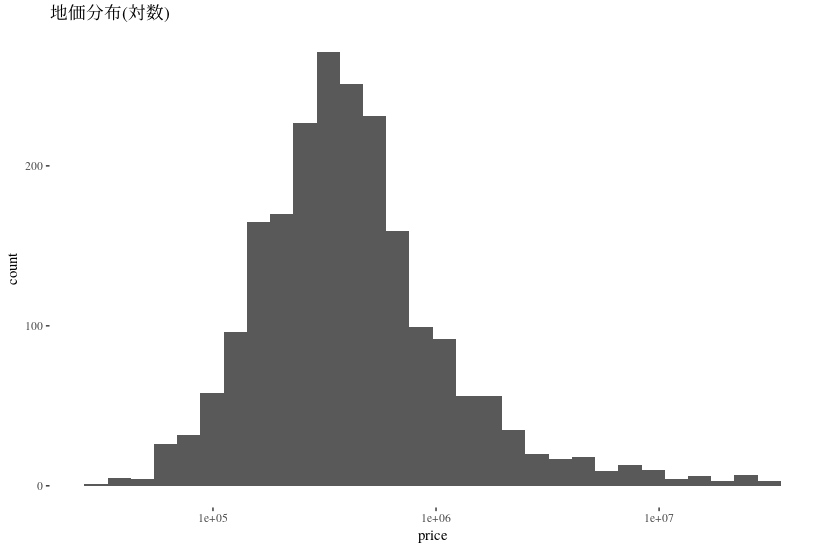
これは地価の対数のヒストグラムである. 変換前の値はもっと歪んだ分布をしており, CAR モデルの分布に合わない可能性が高い. よって, 地価の対数に対して回帰するモデルにする.

さて, CARBayes の使い方だが, Lee (2013, CARBayes: AnRPackage for bayesian spatial modeling with conditional autoregressive priors) の開発者自身による説明は丁寧だが, 古いバージョン準拠である. 最新の ver 5.0 いろいろと変更があるので動かない. 例えば, CARBayes 4.0をつかってみるテスト：Taglibro de H：SSブログでも紹介されている S.independent, S.CARiar が消えていることに注意. そのため, S.CARiar() で instrinsic CAR モデルを推定することができないが, どうやら代わりに S.CARleroux() で特定のパラメータを指定することで使用できるようだ.

そこで, 推定し直してみる*5. 推定結果のRMSEは 2,014,116 となり*6, 決して小さくはない. 残差ヒストグラムは以下のようになる.

f:id:ill-identified:20180813004907p:plain — CAR モデルの残差ヒストグラム

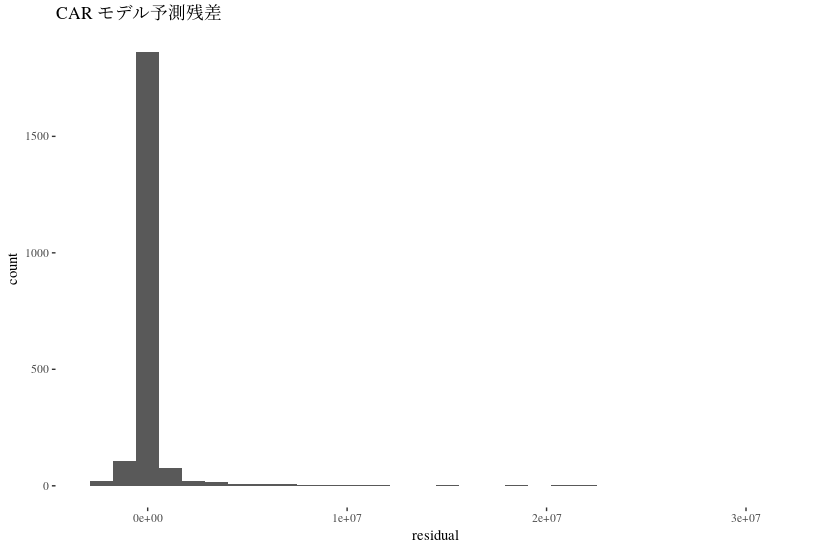
残差がゼロ周辺に手中しているが, 一方で外れ値も目立つ. そこで, 外れ値の原因を見るため, 地図にプロットしてみる.

f:id:ill-identified:20180813005021p:plain — モデルの残差を地図に表示

f:id:ill-identified:20180813005132p:plain — モデルの残差を地図に表示

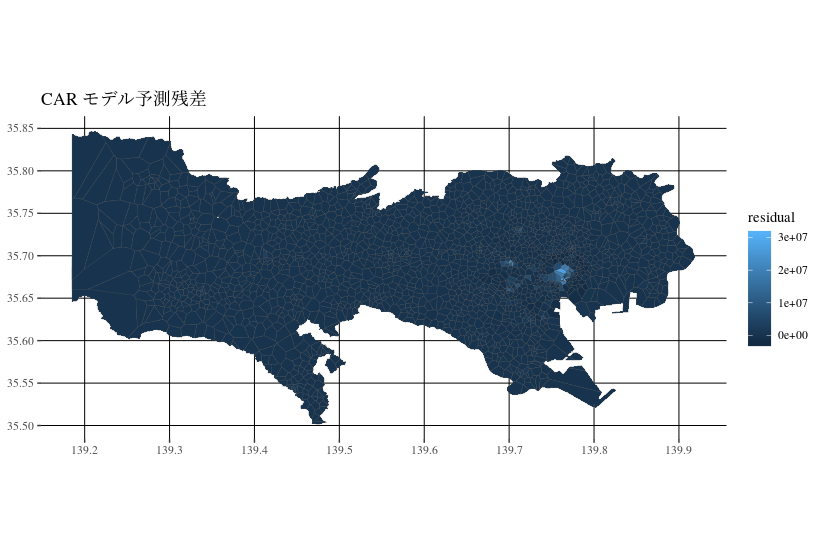
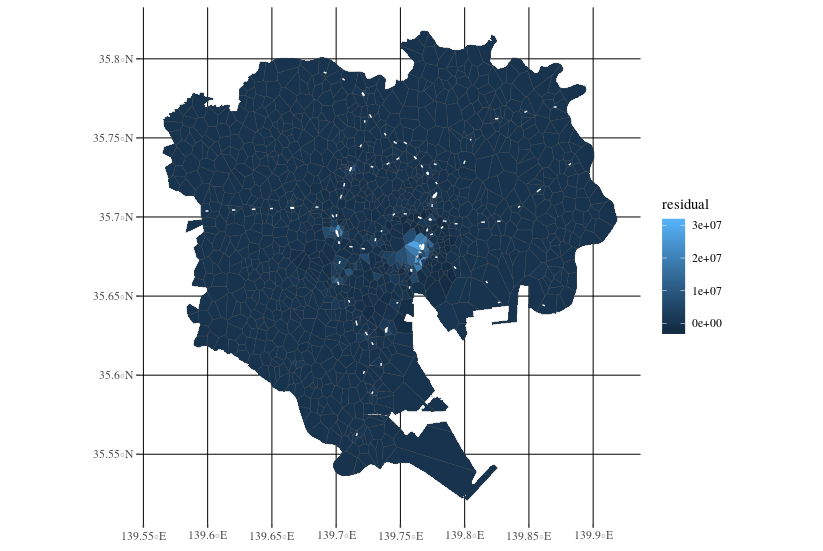
どうやら, 残差の外れ値は都心に集中しているようである. そこで, 23区だけを拡大してみると, どうもこの位置には心当たりがある. ということで, 国土数値情報から平成29年度版の駅情報を取得し, 23区内のJRの駅をオーバーレイしてみた. するとやはり, 外れ値は, 東京駅・渋谷駅・新宿駅・池袋駅といった複数路線のハブとなる駅の場所と一致する*7.

そこで, 今度は, 各ポリゴン内に, 駅が存在するかどうかの情報を追加して推定し直す. さらに, 上に挙げた4駅については, 「ハブ駅」の有無として別の変数を作成した*8.

その結果, RMSE は, 1,814,627 となった. 残差のマッピングは以下のとおりである.

f:id:ill-identified:20180813005314p:plain — 修正した CAR モデルの予測残差を地図に表示

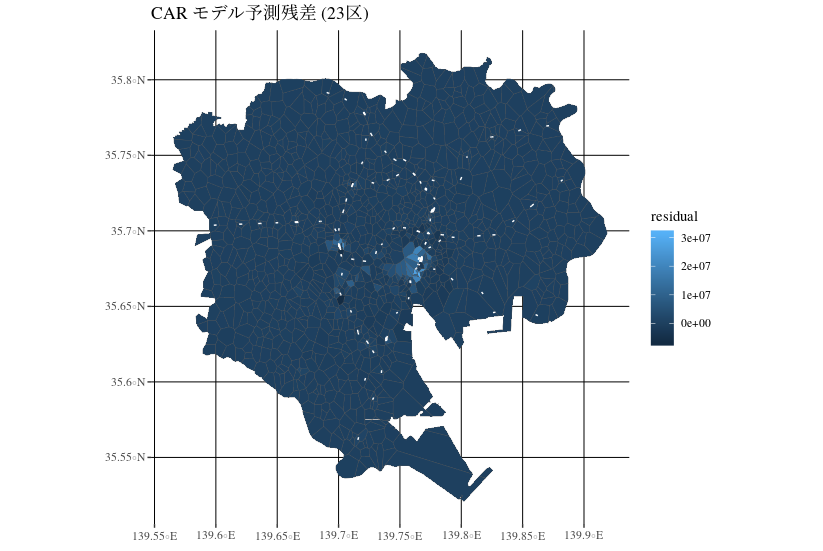
多少ましになっているようだが, まだ新宿と東京駅周辺では外れ値が多いようである.

以上の処理をしていたプログラムは以下の通り. 以前は sp, maptools などに頼っていたが, tidyverse と sf パッケージにより, 前処理がかなり楽になっている. たとえば隣接行列は sf_intersects() 関数だけで作成できる. グラフの多くも, ggplot2 に追加された geom_sf() でかなり簡単に描けるようになっており, 労力はテーブル形式に変換済みのデータを推定用の関数にかけるのと大差ない.

gist3f3331bb0206e67e82823c4c51027358

古いバージョンはここをクリックして展開してください. 現在は不要ですが, 参考として残しておきます.

出力されたポリゴンには, 変換前の点に対応した属性情報が紐付けられているので, これを R に読み込ませる. 以前 [R] Rで学ぶ都知事選のデータ可視化【地理データ編】 - ill-identified diary で書いたように, maptools でR に読み込ませたら, まず隣接行列を計算させる. すぐに隣接関係を出力できる. ポリゴンの隣接関係は spdep::poly2nb() で計算できる. 点と点の距離で判定したいならば, nb2WB() などを使う (rgeos なら gTouches() を使う. ). poly2nb() は隣接情報をリストで返すので, これを matrix 型に変換して, CARBayes::S.CARia() に渡す. CAR モデルの場合, 標準化は必要ないので, 隣接行列の成分 $w_{ij}$ は必ずゼロか1にする*9.

隣接行列を作成したら, あとは CARBayes::S.CARiar() 関数でフィッティングを行う. 空間自己相関モデルで都心の地価を推定した研究に, 唐渡 (2007) というのがあり, こちらはもっといろいろな説明変数を用意しているが, 今回はとりあえず実際のデータを持ってきて動くところを見せられれば, という考えなので, 説明変数は適当である (size は面積である.).

require(CARBayes) # 4.3
require(maptools) # 0.8-30
require(spdep)    # 0.5-88
require(ggplot2)  # 1.0.1
require(ggthemes) # 2.2.1
setwd("~/Documents/blog/20151027_GIS/") # 任意のディレクトリに変更
voronoi <- readShapePoly("out.shp")
# list 型から matrix へ
nbl2mat <- function(x, is.dev=F){
  w <- matrix(0, ncol=length(x), nrow=length(x))
  for (i in 1:length(x)){
    w[i,x[[i]]] <- 1
    if ( is.dev == T) w[i,] <- w[i,]/sum(w[i,])
  }
  return(w)
}
W <- nbl2mat(poly2nb(pl = voronoi, queen = F), is.dev = F)
fit <- S.CARiar(price ~ price + size, data=voronoi@data, family = "gaussian", W=W, burnin = 2000, n.sample = 32000, thin=10)
voronoi$predict <- fit$fitted.values
voronoi$id <- rownames(voronoi@data)
df <- fortify(voronoi)
df <- merge(x=df, y=voronoi[,c("id", "price","predict","region","region_2")], by="id")
df$region_2 <- as.character(df$region_2)
ggplot(df) + geom_polygon(aes(x=long, y=lat, group=group, fill=predict) ) + scale_fill_continuous_tableau() + coord_equal() 
ggplot(df) + geom_polygon(aes(x=long, y=lat, group=group, fill=price) ) + scale_fill_continuous_tableau() + coord_equal()
ggplot(df[grepl("区$",df$region_2),]) + geom_polygon(aes(x=long, y=lat, group=group, fill=predict ) ) + scale_fill_continuous_tableau() + coord_equal() 
ggplot(df[grepl("区$",df$region_2),]) + geom_polygon(aes(x=long, y=lat, group=group, fill=price ) ) + scale_fill_continuous_tableau() + coord_equal()

で, 適当な変数にしたからか全くフィットしていないようだ……

f:id:ill-identified:20151120002047p:plain

f:id:ill-identified:20151120002103p:plain

上:推定結果, 下:実際の値

f:id:ill-identified:20151120002145p:plain

f:id:ill-identified:20151120002153p:plain

上:推定結果 (23区),下:実際の値 (23区)

今回は QGIS の機能をほとんど紹介できなかったが, 地理情報のデータハンドリングに関しては便利な機能が多く存在するので, また別の機会にまとめておきたい.

参考文献

Besag, Julian, Jeremy York, and Annie Mollié. 1991. “Bayesian Image Restoration, with Two Applications in Spatial Statistics.” Annals of the Institute of Statistical Mathematics 43 (1): 1–20. doi:Bayesian image restoration, with two applications in spatial statistics | SpringerLink.
Kissling, W. Daniel, and Gudrun Carl. 2008. “Spatial Autocorrelation and the Selection of Simultaneous Autoregressive Models.” Global Ecology and Biogeography 17 (1): 59–71. doi:Error - Cookies Turned Off.
Lee, D. (2013). CARBayes: AnRPackage for bayesian spatial modeling with conditional autoregressive priors. Journal of Statistical Software, 55(13). doi:CARBayes: An R Package for Bayesian Spatial Modeling with Conditional Autoregressive Priors | Lee | Journal of Statistical Software
Lesage, James P. 1999. Spatial Econometrics. Econometrics Toolbox for MATLAB.
伊東宏樹. 2015. 『時系列・空間データのモデリング』「岩波データサイエンス」, 岩波データサイエンス刊行委員会編, 1巻 pp. 39–59.
岩波データサイエンス Vol.1
- 作者:
- 出版社/メーカー: 岩波書店
- 発売日: 2015/10/08
- メディア: 単行本（ソフトカバー）
唐渡広志. 2007. 『地価関数の推定と空間的自己相関の検出』 土地総合研究 5巻, 4号: 3—13.
間瀬茂. 2010. 『地球統計学とクリギング法 ―RとgeoRによるデータ解析―』オーム社.
地球統計学とクリギング法—RとgeoRによるデータ解析—
- 作者:間瀬茂
- 出版社/メーカー: オーム社
- 発売日: 2010/11/27
- メディア: 単行本（ソフトカバー）