2014/11/20 時事ネタと言いつつ時事ネタへの言及が皆無だったので加筆

前置き

時事ネタ (NHK: 自民党３５人学級見直し反対の決議案) というほど時事問題に踏み込んではいないが, 少人数教育に関する研究として, J. D. アングリストと V. レヴィによる1999年の論文 "Using Maimonides' Rule to Estimate the Effect of Class Size on Scholatic Achievement" をまず連想した. ネット上では日本語でこれに言及されているところは見られなかったので, せっかくだからここで解説することにした. また, 日本での研究事例として, アングリストらの研究と同様の手法を用いた赤林・中村(2011) にも言及した.

まず, アングリストらの研究の概要を書くと, こうなる. イスラエルの公立校のおよそ2000クラスについての, それぞれの生徒数とテストの得点のデータを回帰分析し, テストの (平均) 得点とクラスの生徒数の負の関係を発見した. つまりクラスの人数が少ないほど, テストの得点が向上するということだ. ただし, 回帰分析の係数は必ずしも因果関係の大きさを意味するわけではない*1. そこで, アングリストらは通常の回帰分析だけでなく, 「操作変数法」と「RDD」という2つの手法を用いて推定し, 因果効果のあることを主張した. 特に後者は, イスラエルの公教育制度におけるクラス編成の際の, 1クラスあたりの人数上限ルール, 通称「マイモニデス・ルール」を利用したものである.

マイモニデス・ルールとは

「1つの教室あたりの生徒は25人とし, 多くても40人を超えてはならない」

つまり, ある年の入学者が 40名である場合, クラスは1つだけ, そして入学者が41人なら, 1クラス辺り平均20.5 人のクラスに分けられる. 同様に, 80名なら40人クラスが2つ, 81名ならば 3クラスに分けられ, 1クラスの平均人数は27人, ……というふうに. イスラエルの公立校では1969年以来*2, このルールをクラス分けに用い続けている.

ある学校 $s$ の, あるクラス $c$ の平均人数 $N_{sc}$ は次の式 (以降これを「クラスサイズ関数」と呼ぶ) で表せる.

${\displaystyle N_{sc}=(学年の生徒総数)/( int( (生徒総数 -1 ) / 40 ) + 1 ) }$

$int(\cdot)$ は実数の整数部をとりだす関数である. 1学年1~40人なら, 40, 41~80 なら, 20.5 ~ 40, 81人~120人なら 27~40人…… と言うふうに求められる.

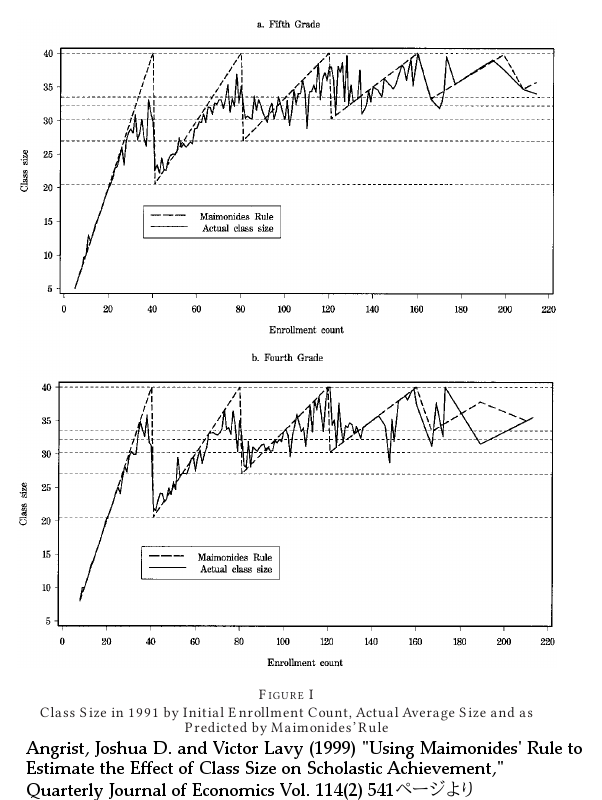
では, 実際のデータはどうなっているか. 実際にはイスラエルのクラス分けは必ずしもこのルールに厳密なわけではなかった. 上記の式で表されるクラスサイズ関数と実際の人数をプロットして比較したところ, 必ずしも一致しなかった. 例えば, ルール上は40人学級も許容されるが, 実際のデータでは40人より少ない学級が編成される場合も観察された. これは多くの学校でもう1つ学級を置く余裕があったことを意味する. 中央値は 31, 25% が35人以上で, 10% が38人以上だった.

図1: 元論文からの転載. 破線がクラスサイズ関数による理想のクラスサイズ, 実線が実際のクラスサイズ (平均値).

f:id:ill-identified:20141116173552p:plain

次に, 学校選択の自由について考える必要がある. もし親が児童を好きな学校に入学させられるなら, 教育が充実していると評判のいい学校に入学させたがるだろう. そうなると「評判のいい学校の持つ高い教育能力」と「相対的に成績の良くない児童」によって効果が打ち消し合い, 正確に結果が導かれない. その点, イスラエルでは越境入学は認められていない (ただし家族ごと移住すれば好きな学校へ入学できる). また, イスラエルでは私立校に通う生徒はかなり少ない. よって, 「成績の悪い児童を評判のいい学校に意図的に入学させる/転校させる」という可能性は薄い. つまり, この事実から, 擬似的なランダム化が成立している, と主張している.

学年の人数, クラスサイズ, テストの平均点をグラフにすると, 明らかにクラスサイズと得点には相関関係があるように見える.

しかし, 学年の人数が多い学校は, 都市部 (=富裕層が多い) に偏り, 逆に小規模な学校は郊外の比較的低所得層に偏っている可能性がある (家庭環境の良くない生徒ほど成績の悪くなる傾向があることは先験的に分かっている). これについては, 後ほど対処方法を述べる.

この学年の人数のトレンドを除去したところ, クラスサイズと得点には負の相関が見られた. つまり, 平均点をクラスサイズで線形回帰した傾きは, 第5学年の読解力テストの得点でおよそ -0.22, 第4学年の読解力テストの得点でおよそ -0.11 となった. つまり, (限界効果が一定でなら), クラス人数が10人減るごとにテストが2.2点良くなる, ということになる. もちろん, 相関係数 = 因果関係の大きさ, と判断しても良い理由も必要であるが.

検証方法

以上のことから, クラスサイズと成績には因果関係がありそうだと考えられる. そこでアングリストらは, これを次のような統計モデルで検証した.

${\displaystyle y_{isc} = \boldsymbol{x}_{s}^\prime \boldsymbol{\beta} + n_{sc}\alpha+\mu_{c}+\eta_{s}+\epsilon_{isc} }$

$\boldsymbol{x}_{s}$ はコントロール変数として, 学校の属性ベクトル, $n_{sc}$ は学校 $s$ のクラス $c$ の人数. $\mu_{c}$ は IIDなクラス単位の誤差項. $\eta_{s}$ は学校単位のそれで, $\eta_{isc}$ が生徒個人単位の誤差項. 今回はクラスサイズの効果なので, 主に興味があるパラメータは $n_{sc}$ の係数 $\alpha$ ということになる.

この回帰式は, 生徒個人単位を記述しており, クラスサイズが生徒個人の成績にどう影響するか, ということを表している. しかし, 今回のデータはクラス単位のデータで, 個人単位のデータはない.

なお, これ以前の少人数教育に対する研究では, 生徒を無作為に編成する「実験」も存在したが, 個人単位でなくクラス単位の実験であったため, アグリゲーションバイアスの問題があった.

上の回帰式を先に示したクラスサイズ関数と合わせ, さらにクラス単位に集計すると, ${\displaystyle \bar{y}_{sc} = \boldsymbol{x}_{s}^\prime \boldsymbol{\beta} + n_{sc}\alpha + \eta_{s} + ( \mu_{c} + \bar{\epsilon}_{sc} ) }$

ここで, コントロール変数 $\boldsymbol{x}_{s}$ には学年全体の入学者数を入れるのだが, 次の4通りの方法で加工してそれぞれ推定する. 入学者数をコントロール変数に (1) 含めない (2) 含める (3) 2次形式 $\beta_{1} x + \beta_{2} x^2$ の形で含める (4) マイモニデス・ルールによるクラス分けの閾値で区切った区分線形関数, とする. 区分線形関数は具体的には,

$\begin{align*} e_{s} & \textrm{if}\, e_{s} \in \left[0,40\right] \\ 20 + e_{s}/2 & \textrm{if}\, e_{s} \in [41, 80] \\ 100/3 + e_{s}/3 & \textrm{if}\, e_{s} \in \left[81,120 \right] \\ 130/3 + e_{s}/4 & \textrm{if}\, e_{s} \in \left[121, 160\right] \\ \end{align*}$

とする.

推定結果

OLSだと, 学年や科目によっては $\alpha$ がマイナスになる場合も存在した. この理由として, 次のような仮説が考えられる.

「生徒の各クラスへの割り当てはランダムではない」例えば私も日本の教育現場で「基本的には無作為にクラス分けするが, あまりにも相性の悪い生徒どうしはクラス分けを考慮することがある」という話を聴いたことがある. アングリストらの場合, 教師にとってのトラブルが起きないよう管理する上での利便性から, 学校生活を送る上で「問題児」を重点的に少人数クラスに割り当てる場合があるのかもしれない, と述べている.

この仮説が事実なら, 少人数クラスにもともと成績の芳しくない生徒が重点的に割り当てられ, 結果として少人数教育の効果が相殺され, 係数が過少に計算されることになる. そのため, なんらかの方法でこの「バイアス」を係数から除去する必要がある. アングリストらは, バイアスの除去のため, 操作変数法と RDD をそれぞれ利用している

RDD とは

RDD とは, Regression-Discontinuity Design のことで, 訳語としては, 「回帰非連続計画」「非連続回帰デザイン」「回帰切断デザイン」など表記にゆらぎがあり, 統一されていないようだ. Campbell (1969) で提案された手法で, サンプルにバイアスがある場合, なるべくバイアスのない部分だけを取り出して推定に用いる方法である*3. 今回の場合, 学年全体の人数と生徒の成績が相関することでバイアスが発生する可能性が指摘されている. それならば, 学年全体の人数が似たようなサンプルの個体だけを抜き出して推定すれば, そのバイアスは回避できることになる. 1クラスあたり40人を超えないようにするには, 学年全体の人数が 41人, 81人, 121人, ……の時点でクラス分けを行えばいいので, サンプル全体からその人数のプラスマイナス数人の範囲のものだけを取り出して推定する.

ただし今回は, 先の図でも見たように, 「学年全体の児童の数が40人を超えるごとに新しくクラス分けする」というルールに完全に従っているわけではない. 実際には40人を超える前に分割している場合もあった. つまり, 新しくクラス分けするかしないか, の判定ルールがあいまい (ファジー; Fuzzy) なのだ. このような場合に適用できる RDD を特に, Fuzzy RDD と呼ぶ (逆にはっきりしている場合は Sharp RDD と呼ぶ). 結論だけ言うと, このような曖昧なルールの場合には, 操作変数を用いることで RDDを適用できるというのが Fuzzy RDD である*4. 今回の場合, 操作変数は, さきほどのクラスサイズ関数から導かれる, 平均クラスサイズの予測値である.

操作変数

すでに書いたように, もうひとつ考えられるバイアスは, 少人数クラスへの児童の割り当て自体にバイアスがあるという話である. 少人数クラスのほうがもともと成績の良くない児童が割り当てられる, そして成績の良くない理由は家庭環境に由来する, というものだった. そこでこの研究では, 操作変数*5として PD指数を用いた. PD指数とは, イスラエル教育省が推計している「学校外での教育資源の大きさ」である. これは児童の親の教育水準や家族構成などから算出される*6.

結果*7, 第5学年では, コントロール変数の選択によらず, どれもクラスサイズの係数は負だった (つまり少人数ほど効果がある). ただし, 読解の点数は有意だったが, 数学の得点は標準誤差が大きく, コントロール変数の追加によって読解の得点の場合と同じ傾向が見られるものの, 有意ではない.

さらに, RDDの手法に基づいて, クラス分けの発生する人数 $\pm 5$ 人に限定したサンプルに対しても同様に推定を行った. つまり入学者数が, 41人まわりの $[36,45$ ], 81 人まわりの $[76, 85$ ], 121人まわりの $[116, 125$ ] の範囲のサンプルである. さらに, $\pm 3$ 人に絞った場合でも結果を示している.

結果, サンプルサイズを小さくした (サンプルサイズは471に減少した) にも関わらず, 被説明変数の数学と読解力に対して, それぞれ入学者数をそのままか二次形式で与えた場合で推定したところ, 数学・二次形式の組み合わせ以外の3つは全て有意になり, 係数自体 -0.41~-0.58 と倍以上大きくなっている.

図2: 元論文からの表IVの転載.

f:id:ill-identified:20141116163827p:plain

第4学年の結果*8は, 第5学年と比べて効果が小さいが, 同様の傾向を示すため, 推定結果の頑健さを示した (ただし2次形式は有意ではない).

また, 入学者数効果についても, 単純に人数を説明変数に加えるのではなく, どのカットオフポイント近傍に存在するかどうかを表すダミー変数 $d_{1sc}, \,d_{2sc}$ をコントロール変数として使用した (元論文の表VI). $\pm 5$ のRDDサンプルで推定したところ, このダミー変数は有意でなく, コントロール変数として意味をなさなかった. つまり, クラスサイズを狭い範囲に絞りこめば, 入学者数の大小による効果は無視できる, ということが示唆される.

さらに, 児童の生活環境とクラスサイズの関係を考慮するため, PD と交差項 $f_{sc}$ , $\mathit{PD}\times f_{sc}$ の2つを操作変数とした (元論文の表VII) 交差項は負で有意だったため, これらから, 少人数教育の効果は, 家庭環境の良くない児童に対して, より大きな効果があるということを強く示唆している.

また, 第3学年については, 同様にクラスサイズの係数は全て負だったが, 有意ではない. これについてアングリストらは, 学年が上がるほど係数の絶対値が大きくなること, そして有意になりやすくなるのは, 少人数教育の効果が累積的なものであるからとしている. 学年ごとの児童の人数はふつう大幅に変動しないから, 少人数のクラスで始まった学年はその後も少人数のクラス編成が続くからではないかとしている.

ただし, 一方で, Krueger (1999) の STAR 計画の再試験においては, 「教育の累積効果」は存在しないとしていることも注意しなければならない.

日本での研究事例は?

以上の結果から, 少人数教育にはある程度の効果があると判断できる. しかし, これはあくまで, イスラエルの公立校を母集団とした場合の結果である. 操作変数法やRDDを用いたことによって, 因果効果を正しく得られた (内的妥当性) としても, これが外国や高等教育でも同じ結果を適用してよいかどうかはまだ解らない (外的妥当性).

偶然だが, 日本でも1クラスあたりの生徒数は40人を上限とするルールがある. これに目をつけた赤林・中村(2011) ではアングリストらの研究と同様の方法を用いてクラスサイズの効果を調べている*9. こちらは 2014年11月16日時点で参考文献のリンク先で一般公開されており, 言語も日本語で, 手法もアングリストらのものを踏襲しているため, ここまでの説明が頭に入っているならそう難解ではない.

赤林・中村の研究では, 情報公開請求制度を利用して, 横浜市内の公立校の学力テスト (国語と算数) とクラス編成の情報を入手している. 分析手法は, アングリストらの研究を踏襲しており, まず OLS で推定するが, やはりクラス編成のバイアスを問題にしている: たとえば習熟度別授業が導入され, 成績で児童をどのクラスへ割り当てるかを決めている場合である. 実際に各学校が習熟度別授業を行っているかどうかのデータはないため, バイアスの原因になりうる. さらに, この研究で入手できた横浜市内の公立校では, 学級編制の弾力化が行われ, クラス編成のルールが緩和されている. やはりアングリストらの研究のように, Fuzzy RDD を適用する必要がある. 少人数・大人数クラスを識別するための操作変数は, やはりクラスサイズ関数によるクラスサイズの予測値である.

また, アングリストらの研究との違いとして, 学年初めと学年末のテストの結果を入手できたことがある. そこで, 赤林・中村らは, 被説明変数に学年末のテストの成績を与え, 説明変数に学年初めのテストの成績を含めるようにモデルを変更した. これは value added (付加価値) モデルと呼ばれるもので, いわば1年間の教育の効果の大きさを推定していることになる. この変更により, より純粋に1年間の教育の成果を推定できる.

結果, OLSでは有意でないが, 操作変数を用いた場合では有意な結果がでやすいという, アングリストらの研究と同じ傾向が見られた. また, 効果じたいの大きさについては, アメリカでの Krueger (1999) での研究とアングリストらのイスラエルでの研究結果を比較すれば, イスラエルの3分の1, アメリカの2分の1 となった.

ただし, 次のような事実にも気をつける必要がある.

ホームルームでのクラスサイズとは別に, 習熟度別授業が行われる科目が存在する
横浜市内のデータのみで推定を行った.
中学3年生のデータでは, 符号がプラスの場合もマイナスの場合もあり, また有意な結果は得られなかった.

(1) については, 算数は習熟度別授業が行われることが多い反面, 国語で習熟度別授業が行われることは少ない, という点に注意する必要がある. 文科省の『平成19・120年度全国学力・学習状況調査追加分析報告書』によれば, 小学校における国語と算数の習熟度別授業の未実施率はそれぞれ約80%, 35%となっている*10. そのため, 横浜市内でも多くの学校が算数科目で習熟度別授業を行っているなら, 有意にならなかったの原因がこれである可能性がある.

(2) についても, 横浜市内という限定的なデータのため, 他の市区町村, 都道府県でも当てはまる結果かどうかは, ここまでの情報では断定できない. そのため赤林・中村らは全国レベルでの学力データの蓄積とアクセスを訴えている.

(3) また, 中学3年の成績についても, クラスサイズ効果は有意ではなかった. これについては, 赤林・中村らは小学生の学年末テストが2月に行われるのに対し, 中学3年の学年末が11月に行われるため, 学年始めと学年末のテストの期間が短いこと, また多くの生徒は受験勉強を行うため, 教育と関係なく自発的に勉強する傾向があるから, という2つの仮説を挙げている.

所感

教育の効果というのは年齢に対して線形ではないのだろう. そして, この非線形な曲線を見つけるには, データの数, つまり全国規模に広めた調査だけでなく, 変数の数, つまり質が不足しているようだ. 今回紹介した2つの研究で, ただし, ただし, といくつもの条件を挟んだ上での主張が多かったが, 社会科学の実証研究においてこういうことは多い. 前述の理由により, 目的の推定値を得るためにもろもろのノイズを除去できず, 例えば力学のようにシンプルな因果関係を見つけられていないのが現状だからである.

だが, アングリストらの研究で最も特筆すべきなのは, クラスサイズ効果の大きさというよりもむしろ, 大規模で手間も費用もかかる実験環境 (今回の例で言うなら STAR 計画) を整備しなくても, かなり信頼できる推定が可能である, ということだ*11.

このようなアプローチは, もちろん学校教育の効果の分析にしか使えないわけではない. 学術研究一般, 政策を決定する場合全般, そしてさらに民間企業での新しい施策, 事業を打ち出す際の意思決定にも, 応用の可能性があるのではないか.

現実の政策への応用

また, ここから得られる現実の政策への応用についても述べたい (ここからは, 完全に筆者個人の主張で, ここまでで挙げた研究者の意見とはまったく関係ない).

発端となったニュースだが, 「学級編制の上限を35人から40人へ増加させよ」という提言である. 財務省の提言ということだから, 教育予算の削減が, この政策実施に対する効果なのだろう. しかしながら, ネット上のいくつかのニュース記事を見る限り, これに賛成する側も反対する側に (反対する側の声がかなり多いように見える) も, 客観性のある論拠が少ないように感じる*12.

例えば, 「アンケート調査で国民のどれくらいがこの政策を支持しているか」や「海外ではこれだけ教育に予算を投じている」といった資料は, 政策の判断材料としてほとんど意味をなさない. 前者は, 他人がどう考えているかと自分の判断は関係ないし, 後者について言えば, 今回の研究で示唆されたように, 国によって教育効果の推定結果はかなり異なることから, 国際比較は無意味である. その政策をすべきかすべきでないか判断がつかない人に対しては, その政策のメリット・デメリットを提示すればあとは勝手にその人が自分の価値観に基づいて判断するだけの話だろう.

では, 今回のアングリストらの研究, あるいは赤林らの研究は, この政策の是非に対する判断材料となるだろうか? 正直に言うと, これらの研究を持ち出すのは適切ではない. なぜかというと, いずれの研究も, 日本国内全体のデータを用いた推定結果ではないからである. もちろん, 以前書いたように, 統計的には全数調査ではなく, サンプリング調査でも推定できる. しかし, アングリストらの研究と赤林らの研究では係数が大きく違うことから, 国ごとに差異があるのは明らかだし, どうように地域によっても係数が変わる可能性がある. よって, 横浜市だけを対象にした赤林らの研究結を国内全体にも当てはめるのは早計である.

RDD を用いた分析は, 実験環境を用意しなくても行える, という強みがある. 例えば日本国内全体の効果を調べたければ, 横浜市から得られたデータを同様に各都道府県から収集できれば可能である (国や地域ごとの差異を単なる「国民性」とか「文化の違い」といったあいまいな理由で結論付けるのではなく, その奥にある, それ以上分解できない最小の因子を見つけ出すのがこういった研究の究極の目標である.).

実は, RDDには, その原理上もうひとつ, 今回の政策の判断材料として不適切となる点がある. これは次回のRDDの説明でも言及する.

補足: STAR計画とは

アングリストらの研究で言及された, STAR計画 (Project STAR) とは, 80年代にアメリカ, テネシー州で行われた, 教育の効率性のための大規模な実験である. この計画のもとでは, 生徒がランダムに, 大きさの異なるクラスに編成された. この計画では, 幼稚園児をサイズの異なるクラスに編成して, 4年間観察を行った (Hanushek, 2006). 観察対象となったのは約6000人の児童である. 先に書いた, 人間を対象とする実験は実行するのが難しい, という話とは矛盾するが, とにかくアメリカはこのような大規模な実験をやってのけた. なお, この計画で得られたデータをもとに分析した結果についても, やはり少人数のほうが大人数より効果があることが示唆されていた. ただし, 先にも言ったように, 教育の累積的な効果があるかどうかはわかっていない

参考文献

Angrist, Joshua D. and Victor Lavy (1999) "Using Maimonides' Rule to Estimate the Effect of Class Size on Scholatic Achievement," Quarterly Journal of Economics, Vol. 114, No. 2 pp. 533--575
Angrist, Joshua D. and Jörn-Steffen Pischke (2009) "Mostly Harmless Econometrics: An Empiricist's Companion," Princeton University Press, 邦題『ほとんど無害な計量経済学 − 応用経済学のための実証分析ガイド』大森義明, 田中隆一, 野口晴子, 小原美紀訳

「ほとんど無害」な計量経済学―応用経済学のための実証分析ガイド

作者: ヨシュア・アングリスト,ヨーン・シュテファン・ピスケ,大森義明,田中隆一,野口晴子,小原美紀
出版社/メーカー: エヌティティ出版
発売日: 2013/05/31
メディア: 単行本
この商品を含むブログ (1件) を見る

Mostly Harmless Econometrics: An Empiricist's Companion

作者: Joahua D. Angrist,Jorn-steffen Pischke
出版社/メーカー: Princeton Univ Pr
発売日: 2008/12/15
メディア: ペーパーバック
購入: 4人クリック: 12回
この商品を含むブログ (4件) を見る

Campbell, Donald T. (1969) "Reforms as Experiments," American Psychologist Vol. 24, pp. 409--429
Hanushek, Eric A. (2006) "School Resources," in Handbook of Economics of Education, chapter 14, pp. 866--908
Krueger, Alan B., "Experimental Estimates of Education Production Functions," Quarterly Journal of Economics, 114(2), pp. 497–532
赤林英夫・中村亮介 (2011) 『学級規模縮小が学力に与えた効果の分析―横浜市公開データにもとづく実証分析―』 KEIO/KYOTO GLOBAL COE DISCUSSION PAPER SERIES, DP2011-005
文部科学省(2009)『平成 19・20 年度全国学力・学習状況調査追加分析報告書』 (本文は国立教育政策研究所にあり)

*1:因果推論の話はきりがないのでここではしない.

*2:現在は不明

*3:RDD についての厳密な話を始めるとかなり冗長になるため, それは別の記事でまとめることにする. 参考文献として, Angrist and Pischke (2009) を挙げておく.

*4:Fuzzy RDD の具体的な方法についても別の機会に述べることにする.

*5:操作変数法については, すでに情報が多いと思うので解説しない

*6:詳しく解説している参考文献がヘブライ語なので詳細不明

*7:元論文の表IVに対応

*8:元論文の表V

*9:クラスサイズの効果に関する国内の研究自体はそれ以前にも存在する. 詳しくは赤林・中村 (2011) で言及されている文献を参照

*10:全国平均であることに注意

*11:このような手法を自然実験とか準実験とか呼ぶ.

*12:もちろんどの政策を支持するかは個人の信条次第である. しかし, メディアで発信するのだから質の高い「判断材料」を提示して欲しい, という気持ちがある

ill-identified diary

所属組織の見解などとは一切関係なく小難しい話しかしません

[時事ネタ] 少人数教育は実際どれくらい意味があるのか

前置き