2024/4/22: 先行研究とゴルトン゠ワトソン分枝過程の解説の追記
2024/4/23: 多数の言い回しのおかしい箇所の校正
2024/4/24: グラフ上の記載ミスとグラフ描画コードを修正
この記事の要約
- 先日報道された「500年後に日本人が佐藤だけになる」という試算の内容に違和感を覚えた.
- 資料を確認してみると, 大きな問題のある方法で試算がなされていることがわかった.
- 苗字の絶滅問題について, より実現可能性の高いシナリオをシミュレーションし, そのプログラムと結果を公開した
- 報道された試算とは大きく異なる結果を得られた
- より精緻な分析を行いたいが, 技術的・計算リソース的なハードルに阻まれている
- なんか良いアイディアあったら教えてください
注: 本稿のシミュレーションはまだ完了していません. 先日, 「500年後に日本人が佐藤だけになる」という試算がとある研究機関から発表されたという話を耳にした. しかし, 研究機関のWebサイトが見つからないため, 直接出しているプレスリリースやレポートを確認できない. そのため各種ニュースサイト等で書かれていることを元に判断せざるを得ない. 検索してすぐ見つかるものを適当に列挙する. 各サイトで共通する見解は, 以下である. さて, これは私の素朴な疑問であるが, 記事の筆者に専門的な知識がなかったとしても, 自分で書いていて違和感を覚えなかったのだろうか? 記事で紹介されている試算に問題があるという指摘をしている人を見つけたので引用しておく.
はじめに
佐藤姓が増えるにつれて、佐藤姓の出生率の相対的高さを生み出していた要因が平均に近づくから、同じ伸び率が続くはずがありません。むしろ、消えて行く絶滅危惧姓がどの程度あるか、夫婦別姓によってどう変わるか、もっとまともな試算を出した方が良かったのではないでしょうか。
大湾秀雄 (早稲田大学教授, 日経新聞Web上でのコメント)
「佐藤姓が100%になる3310年、「ただしこの時、日本人口は22人と推定される」と。つまり、22人の佐藤さんだけが住んでいる日本になるわけです。姓の多様性ももちろん大切であり、維持しなければならないと思う一方で、人口22人となってしまえば佐藤さんも何もないわけで、少子化対策の重要性を改めて感じる記事でもあります。
真鍋弘樹 (朝日新聞編集長, 朝日新聞Web上でのコメント)
2つ目に引用した真鍋氏は朝日新聞内部の人間らしいが, 朝日新聞の記事に対してツッコミを入れているのが面白い.
この2名が私の考えている問題点をほぼ代弁してくれたので, 指摘されている問題について, もう少し細かく書くことにする.
まず, (1) のシミュレーションの目的がおかしい. 夫婦別姓であってもなくても, 結婚によって苗字が新たに増えることはない. どちらを選ぼうが, いつかは佐藤以外絶滅する運命であり, 試算が正しいとしても, 佐藤以外が絶滅するのが500年後になるか, 1000年後になるかの違いしかない. 夫婦別姓のメリットをその程度のものとして扱って, 本当に良いのだろうか?
次に, 大湾氏が指摘するように, (2) の試算の方法に問題がある. この試算は佐藤姓の増加率が一定と仮定しているようだ. いくつかの新聞ではグラフ資料が引用されており, それらを見ると, 等比数列, つまり複利計算と同じ要領で計算されているらしい. つまりこれは, 佐藤姓が未来永劫際限なく増え, やがて現在の日本の人口すら突破してしまうような試算である. それに, 前提となる「佐藤姓の増加率が一定である」ことは絶対にない. 夫婦同姓ならば, どちらか一方の姓が子どもに引き継がれるのだから, 佐藤姓が増えるにつれて増加率も変わるはずだ. 直感的には, 佐藤姓が増えるほど, 増加率は加速していくように思える1が, 日本の未来の全てのカップルについて, 誰が結婚するか, 結婚した時にどちらの性が選ばれるかを, 我々は知ることができない. いずれにしても, ここ数年の増加率が今後も維持されるという想定は, かなり無理があるのではないか.
この試算の矛盾について, さらに厳密に堅苦しく説明することもできるが, 読者は求めていないと思うので有名なあの風刺画を取り出すことにする.

そして, 最後の (4) を取り上げているメディアは少ない. 日経新聞は, 夫婦別姓を許容した場合に, 絶滅が先送りされるが, その頃には日本人の人口がほとんどなくなる, という趣旨のことに少しだけ触れている. 朝日新聞は, この事実が書かれたグラフを引用しているが, 本文では全く言及していない. そして, 冒頭で引用したように, 朝日新聞の記者とは別の人物がツッコミを入れている. 上記に挙げた他のサイトでは, この問題は全く言及されていない. なぜ人口が減っているのかは全く触れられていないが, 人口問題であるからには, 佐藤姓の増加率と同じく, 現在の出生率や人口減少率がそのまま続くと仮定した試算ではないかと思われる. しかし, 日本の人口がたった数十人になってもまだ佐藤以外の姓が絶滅していないという結果を, 夫婦別姓のメリットだと考える人が果たしているのだろうか.
記者が誤解したのかもしれないし, 発表されたのが4月1日であるため, エイプリルフールに関連したなにかと考えて面白おかしく取り上げているのかもしれない. いろいろ疑念があるが, 研究機関の公式なレポートが見つからないため, これ以上は判断できない. 確実に言えるのは, 上で取り上げた各サイトの記述が全く論理的ではないということだけだ.
問題点の要約
つまり, 「500年後に日本人が佐藤だけになる」という試算が報道の通りの内容であれば, 以下のように二重に問題がある.
- 夫婦同姓制のあり方という問題提起に対する主張のために, 同姓・別姓に関わらず増えることのない苗字の絶滅危惧という, 論点の合わない話題を出している. 加えて, この試算では日本人そのものが絶滅寸前になるという, はるかに深刻な問題を軽く扱っている.
- 現代の日本の結婚制度ではありえない方法で結婚がなされた結果, 苗字が増減するという想定の試算であり, 数字に信憑性がない.
私個人は選択的夫婦別姓にはどちらかというと賛成している. 仕事の利便性から, 結婚後も旧姓を通称として名乗り続けている人間を男女どちらも知っている. しかしパスポートや戸籍など公的文書はそうもいかない. 学生時代に経済学をかじった人間として, 経済学者の奥野(藤原)正寛氏が, 結婚ではなく養子縁組が理由ではあるが, 戸籍上の姓が変わって不便に感じた当事者としてこの問題について言及していることを知っていることも影響している.
選択的夫婦別姓の是非を論じるほど強く支持も反対もしていないのでこれ以上深入りしないが, 最後に1つだけ言っておきたい. もし選択的夫婦別姓の導入を本当に支持しているのなら, このような稚拙な論理を根拠に主張するべきではないだろう.
追記: 発表機関の公式なレポートが公開されている場所を見つけた.
https://think-name.jp/assets/pdf/Sato_estimation_yoshida_hiroshi.pdf
レポートによれば, 対応する将来の人口は「日本の将来推計人口」 による値を引用したのみで, 苗字の多様性と人口増減が相互にどう影響するかは, この試算では考慮されていないようだ. ちなみに, 夫婦同姓を続けた場合の試算で佐藤姓だけになるとしている2531年は, 「日本の将来推計人口」では日本人口が約28万人になる. 残念ながら, 上記の各サイトでの紹介は, 元の分析レポートの趣旨をほぼそのまま反映したものであり, 記者が誤解して紹介していた可能性はなくなった.
(追記) 先行研究について
最初に公開したときは, 後述するTwitter上での投稿しか先行事例を書いていなかったが, 先行研究の簡単なサーベイをここに加筆する.
この記事公開後に, こういう指摘をもらった
twitter.comGalton-Watson分枝過程でモデリングする(≒各親の名字を継ぐ子の人数がi.i.d.と仮定)と、出生率=2の下で各名字はほとんど確実に消滅し、最後の1名字が残る時間がだいたいO(N)≒1億世代であることが言えますね。(cf. https://t.co/IPpRtjW3gd, https://t.co/dNkrWleshU, https://t.co/ApC8OxrId8
— 存在の耐えられない重さ (@genkinanodesu) 2024年4月21日
そういえばそういう話があったなと今更思い出したので, ゴルトン゠ワトソン分枝過程と他に適切な先行研究がないかを軽く調べ直したところ, 普通にいくつも見つかってしまった. 私が当初この記事でやろうとしていたものでは, 以降のシンプルなシミュレーションは導入に過ぎず, 後半で書いているような条件をいろいろと追加したシミュレーションを行うことだった. しかし, 大規模な乱数シミュレーションの技術的課題ばかり考えていたため, こういった確率過程を使ったモデルの話を掘り下げるのを忘れていた (言い訳).
指摘されたゴルトン゠ワトソン分枝過程とは, フランシス゠ゴルトンが最初に研究を始めたモデルで, 家系が何世代後に断絶するか, またその確率はどれくらいかという, まさに今回のテーマと同じ問題意識から発生しているらしい. ゴルトン自身はこの問題の答えにたどり着けなかったらしいが, ゴルトンといえば回帰分析という言葉を生み出すなど, 現代統計学の元勲の一人といえる人物で, かなり歴史のある研究テーマということになる. 分枝過程の話は, この後の理論分析のセクションにもう少し詳しく追記する.
さらに改めて確認すると, 日本国内に限定しても, 確率モデルに基づいた苗字の絶滅問題について扱った先行研究や資料がいくつも見つかった.
- 塩沢裕一『分枝過程の絶滅問題』は, 分枝過程を知らない人向けの資料としてよいだろう. 高校生向けの公開講座のために作られたスライド資料らしい.
- 戸田明志 『将来の日本における苗字の多様性についてのシミュレーション』はエージェントベースのシミュレーションを行っている. なお, この研究では, 夫婦別姓は苗字の多様性の維持に大きな効果はないとしている.
- 佐藤葉子・瀬野裕美 『姓の継承と絶滅の数理生態学―Galton-Watson分枝過程によるモデル解析』は, まだ内容を確認していないが, 目次を見ると理論モデルと実証研究の両方を紹介している書籍のようだ.
特に2つ目のスライドは, 細かい仮定をおき, かつ様々なシナリオを想定して複数のシミュレーションを実施している. これだけ豊富な先行研究があるのに, なぜ冒頭のようなおかしな試算を発表してしまったのか, 謎が深まる…
GARCH(っぽい)モデルによるシミュレーション
頭の「佐藤姓だけになるシミュレーション結果」の報道を信じるなら, これはかなり問題の多い試算である. 以降では, 未来の日本では佐藤姓だけになってしまうのか, それ以外の苗字だけになってしまうのか, という問題をシミュレーションで検証するなら, どうしたらより好ましいかということと, その結果を紹介する.
この報道に関連して, 過去にも苗字の絶滅問題についてシミュレーションをしている人がいることを人づてに知った.
twitter.com「将来、名字って減る一方なんじゃないの?」という長年の疑問を解決すべく、非常に単純化された婚姻-出生-世代交代モデルによる乱数シミュレーションを実行したところ、
— としゅきー™ (@toshchy) 2022年6月18日
約61億年後、日本人は全員 #佐藤 になる
という結論が得られた。
全国の佐藤さん、おめでとうございます。 pic.twitter.com/rZpH1gmuaU
リプライツリーを辿った限りでは, シミュレーションに使用したプログラムなどは公開されていないが, 投稿者である「としゅきー」氏が方法をかなり詳細に解説している. 分かる範囲では, 結婚は完全にランダムに二人のペアを組み合わせる想定のように見える. もしそうであれば, ランダムウォークのような, 長期になるほど結果の不確実性が増す現象となり, 多数派である佐藤や鈴木が絶滅し, マイナーな姓が日本人の全てを占めてしまう可能性が高くなるようなシミュレーションだと予想できる.
- 現在使われている日本人の苗字を人数上位から数万種類選び, 各苗字別人口をシミュレーションの初期値として設定する.
- の全ての人間が結婚すると想定して, ランダムで結婚する人間のペアを選ぶ.
- 単純化のため, カップルは必ず子供を2人生むと想定し, 子供は両親のどちらかの苗字を引き継ぐ.
- (1-3)までを世代交代時の手続きとして, 何世代も計算を繰り返す2
シミュレーション前の理論分析
シミュレーションを始める前に, 理論的に導き出せる結論がないか予め考える.
注: 何言ってるのかわからんって人はなんかグラフがたくさん並んでるとこまで飛ばせばいいと思います. または, どこがわからないか私に教えてください.
このシミュレーションは粒子フィルタを連想するかもしれないが, シミュレーション中に粒子が新たに発生することはない. 直感的には, ランダムウォークのような, 長期分散が発散する不安定な時系列になりそうだが, 陽に表すのがかなり大変そうである. だが, 分布が決まっているので, 実際の計算はギブスサンプリングと同じだろう. シミュレーションの前に, もう少し理論上の挙動を考察してみたい.
最初の世代交代は, 全員がペアを作り結婚し, どちらか一方の苗字になる. よって, ペアがランダムであるなら, 結婚後に残る苗字の数は, 現在の苗字別人口から, 試行回数を人口のちょうど半分を無作為に選んだ結果に等しい.3のような操作の結果, 選ばれる苗字は多変量超幾何分布に従うはずだ. 現在の苗字別人口のベクトルを , 最初の総人口を
とすると, 分布を
で表せる.
とすれば, 結婚で同姓が適用された後の名字別人口はその半分の
である. 子どもが常に2人生まれるという仮定なので, 次世代の苗字別人口
の期待値は, これを2倍したものに等しく, 結局
に等しくなる..
次の世代交代後の苗字別人口 もまた人口比に比例した多変量超幾何分布分布になるので,
で条件付ければ期待値は前世代と変わらない.
よって, 繰り返し期待値の法則を適用すれば, 同様に何世代交代しても, 世代後の苗字別人口の期待値
は
で一定であるとわかる.
次に分散4を考える. 多変量超幾何分布 の分散を
と表す. 子どもの数はカップルの数の2倍なので, 分散は
倍したものに等しい. よって, 次世代の苗字別人口
の分散は
と表せる.
さらに次の世代での結婚後の苗字別人口は となる. 同様にこの分布の分散を求めて4倍すれば, この世代の子どもの苗字別人口がわかる. 分散は分散分解定理を適用して求められるが, 期待値より複雑になる. 式が複雑になるので, 対角成分だけ書いておく.
今回は が非常に大きいため, 世代交代ごとに分散が増加する可能性が高い.
なんかもう眠いので計算間違えてる可能性があるが実際にシミュレーションすればわかるだろう
以上から, このシミュレーションで扱うモデルは, 期待値が一定で, かつ分散が世代を重ねるごとに増大することがわかる. よって, 「ベクトルGARCHモデル」と名付けることにした. ARCHモデルとは, 数理ファイナンス分野などでよく使われる自己回帰条件不均一分散モデルのことである. 上記の式では定数項が存在するため, 一般化ARCHモデル, つまりGARCHと表現した.
- 結果は確率に依存するため, どの苗字が最後まで残るかを確定的に予想できない
- 何世代交代しても, 苗字別人口の期待値は現在と同一で一定だが, シミュレーションする世代交代の数が多いほど, 分散が増大する. つまり, 現時点で人口の多い苗字が絶滅することもありえるし, 人口の少ない苗字が生き残ることもありえるため, 予測が難しくなる.
選択的夫婦別姓との比較
このGARCHモデルは夫婦同姓を想定しているため, 子どもの苗字が両親のどちらか一方になる. 夫婦別姓を採用した場合, このシミュレーションをどう修正するべきか考える必要がある. しかしながら, 両親あるいは子どもがどちらの苗字を選ぶかの意思決定は人それぞれであろう. 法則がわからなければ, シミュレーションすることが難しい. もし, 2人の子どもが必ず, それぞれ異なる苗字を選ぶなら, 苗字別人口が一定となり減らないことは自明であり, シミュレーションをする必要はない. それぞれ選ぶ苗字が完全にランダムならば, 上記の分散の値が少し変わるだけであり, 本質的な違いはない. 最後に, あまり現実的には思えないが, もし, 全ての人間がマイナーな苗字だけを選ぶなら, おそらく苗字の多様性はなかなか減らないだろう. 最後のケースはシミュレーションで確かめてみたいところだが, 後述するように時間がかかりすぎるため, 今回は検証していない.
(追記) ゴルトン゠ワトソン分枝過程について
すで書いたように, ゴルトン゠ワトソン分枝過程 (以下, 単に分枝過程と呼ぶ) という, 今回と同じ問題に取り組むためのモデルが以前から考案されている. ゴルトン゠ワトソン分枝過程 (以下, 単に分枝過程と呼ぶ) では, 各個体が子孫を残す確率が独立かつ同一の分布である (i.i.d.) であると仮定している. 本来は1つの家系をモデル化したものだが, ここでは同じ苗字を持つ人間のグループに置き換えられる. 世代のある苗字の人口を
とすると, 以下のような再帰式で定義される.
は,
世代のある個体
が残す子孫の数を表している. 個体数は確率で変動するため, 各世代での数は不定である. 個体が世代をまたいで生き残ることはない点は, 今回の単純化したシミュレーションと同じ想定である. 分枝過程を視覚的に表現すると, 一定間隔で, ランダムに枝分かれするネットワークが, ある時間が経過した後には何本に枝分かれしているかを表現するモデルといえる. その例が 以下の図である
グラフを描画するコード
import numpy as np import pandas as pd from plotnine import ggplot, aes, geom_segment, geom_point, annotate, labs, theme, element_blank rng = np.random.default_rng(42) nodes = [ pd.DataFrame({'t': [1, 1], 'y': [-4, 4], 'yparent': [0, 0] }), pd.DataFrame({'t': [2, 2, 2, 2], 'y': [-5, -3, 3, 5], 'yparent': [-4, -4, 4, 4]}), pd.DataFrame({'t': [3, 3, 3, 3, 3], 'y': [-4, -2, 3, 4, 6], 'yparent': [-3, -3, 3, 5, 5]}) ] nodes = pd.concat(nodes) ( ggplot(nodes) + geom_segment( aes(x='t-1', xend='t', y='yparent', yend='y') ) + geom_point(aes(x='t', y='y'), size=5) + annotate('point', x=0, y=0, size=5) + labs(x='世代', title="分枝過程の視覚的な表現") + theme( axis_title_y=element_blank(), axis_text_y=element_blank(), axis_ticks_y=element_blank() ) )

各世代で生まれた人間はノード (黒点) で表され, 親子関係はノードをつなぐ線で表される. 今回のシミュレーションに当てはめるなら, 例えば第2世代で途切れている枝は, 結婚により相手の姓に変化したため, これ以降はこの苗字の子孫を残せなくなったとみなせる. 第3世代で枝分かれしていない枝は, 1人だけ子孫を残したことを意味する. 今回のシミュレーションでは, 単純化のため子どもは必ず2人という仮定で計算しているが, 分枝過程では子どもの数がランダムに変化する場合にも対応できる.
この例では1人の個体から増加していっているが, 今回のシミュレーションは第0世代ですでにおよそ1億2千万の個体がいることになる. 一人一人が結婚するかしないかがランダムであり, かつ結婚した場合はかならず2人の子どもを残すという仮定なので, 一人が残す子どもの数は2か0のどちらかであり, 期待値はおよそ1になる. 分枝過程で1人が残す子どもの数の期待値が1以下である場合, 将来のその家系はほとんど確実に絶滅する. さらに, 期待値がちょうど1ならば, その絶滅までの世代の確率オーダーは現在の個体数と同じである.
よって, としゅきー氏のシミュレーションではなく分枝過程を想定した場合は, ではおよそ1億世代くらいで他の全ての苗字が滅亡する可能性がある. 後半のシミュレーションでは最後まで見届けることはできなかったが, 多項分布による近似では, 数千万から1億世代くらいで苗字1種類を残して絶滅しており, 結果的に分枝過程による理論解と近い結果となっている. 分枝過程は1つの家系だけを切り取って考えているという点が, 今回のシミュレーションとは異なる. 今回のとしゅきー氏の方法に基づいたシミュレーションでは, 総人口は一定であるため, いわば苗字の異なるグループどうしが「パイの取り合い」をしているため, 子孫を残す確率が互いに独立していないため, 厳密には分枝過程の条件を満たさないと思われる.5. そのため, このシミュレーションはむしろ, 分枝過程を拡張した「捕食者・被捕食者 (Predator-Prey) 過程」のほうが近いかもしれない.
人口の増減を取り入れたシミュレーションをするなら, 先行研究で取り上げた戸田の研究のように, 人口の増減スピードが現実の日本のものと同じになるよう分枝過程の出生率パラメータを調整してからおこなうと, 現実的な結果が得られそうだ. しかし, これも現実の人口と同じスケールで行うには, 計算量が多すぎる.
一般的な分枝過程の解説は, 先行研究のセクションで示した簡単なバージョンの他に, 以下がある. 他に日本語で細かく解説した資料がどこにあるかは知らない.
使用するデータ
苗字別人口は『名字由来net』の全国名字ランキングの1位から40000位までをそのまま丸ごと取ってきたものである.5 このサイトはユーザー投稿も受け付けているようで, どこまで信頼できる数値なのか判断する情報はない. だが, マイナーな苗字の順位まで大量に掲載されているため, 採用することにした. 順位を見られるのは40000位まである. しかし今回は, 計算時間の問題から, 上位100位までに削減してシミュレーションを行った. 後のセクションで詳細に述べるように, このシミュレーションは非常に計算量が多く, 普通のPCではとても時間がかかるので, いろいろと妥協している.
ライブラリの読み込みや基本設定など
from pathlib import Path from typing import Iterable, Optional import pandas as pd import numpy as np import scipy as sp from tqdm import tqdm import time from multiprocessing import Pool from plotnine import * from adjustText import adjust_text from mizani.formatters import percent_format, comma_format SEED = 42 N_PARALLEL = 4 OUTPUT_DIR = Path('name/output') rng = np.random.default_rng(SEED) theme_set(theme_classic(base_family='Noto Sans CJK JP'))
from surname_sim.loader import load_dataset d_myoji_full = ( load_dataset() .assign( t=0, rank=lambda d: (d.index + 1).astype(int), number=lambda d: d['number'].astype(int)) ) d_myoji = d_myoji_full.iloc[:100]
上位100種類までの合計は 40287000 人となる. 統計局による2023年10月時点での人口推計値6である1億2397万人と比較すると, 約 32.5 %に相当することになる. ちなみに私の苗字は上位4万件に含まれているが, 親の旧姓は含まれていない.
取得したデータの特徴を, 簡単に確認する. 図 2 は苗字別人口の偏りをパレート曲線で表したものである. 曲線が斜線に近いほど, 苗字別の人口の分布は均等になっていることになり, 曲線が左下に張り付いているほど, 偏りが大きいことになる.
グラフを描くコード
def tmp(data:pd.DataFrame): d_pareto = ( data.sort_values(['number'], ascending=True) .assign(cumsum =lambda d: d['number'].cumsum()) .reset_index(drop=True) ) return ( ggplot( d_pareto.reset_index().assign(index=lambda d: d.shape[0] - d['index']), aes(x='index', y='cumsum')) + geom_line() + geom_abline(intercept=d_pareto['number'].sum(), slope=-d_pareto.number.sum()/d_pareto.shape[0], linetype=':') + labs(x='苗字別人口の順位', title='名字別人口のパレート曲線(?)', subtitle=f'『名字由来net』全国苗字ランキング掲載の上位{d_myoji.shape[0]}位から作成') ) tmp(d_myoji_full).show() tmp(d_myoji).show()


「日本で一番多い苗字は佐藤と鈴木である」というのは昔から言われているので私も聞いたことがある. 今回取得したデータでも, 以下の 図 3 のように, この2つの苗字が多さにおいて1位と2位であった. しかし, 最も多いと言っても, どちらも全体の1.5%程度である.
グラフを描くコード
def tmp(data:pd.DataFrame)->ggplot: d_rank = ( data.sort_values(['number'],ascending=False) .reset_index() .assign(surname = lambda d: np.where(d['index'] < 10, d['surname'], 'その他')) .drop(columns=['index']) .groupby(['surname']).sum() .reset_index() .sort_values(['number'], ascending=False) .assign( surname = lambda d: pd.Categorical( d['surname'], list(d.loc[lambda d: d['surname'] != "その他"]['surname'][:10]) + ['その他'], ordered=True ) ) ) d_rank['ratio'] = d_rank['number'] / d_rank['number'].sum() return ( ggplot(d_rank.loc[lambda d: d['surname'] != 'その他'], aes(x='surname', y='ratio')) + geom_bar(stat='identity') + scale_y_continuous(labels=percent_format()) + labs(title="40000位内での人口上位10苗字の占める割合", subtitle=f'『名字由来net』全国苗字ランキング掲載の上位{d_myoji.shape[0]}位から作成') + theme(axis_title_x=element_blank()) ) tmp(d_myoji_full).show() tmp(d_myoji).show()


先ほどの数理的な分析から, 世代交代を重ねるほど, 苗字別人口分布の不確実性が増す可能性が高い. 一方で, 現在の人口で最大多数派である佐藤や鈴木でも, それぞれ全体の2%に満たない. そのため, どの苗字であれ, 単一の苗字が支配的になるには相当な時間が必要だろうと予想される.
シミュレーションの技術的な補足
実装は, なるべく多くの人が読みやすいよう Python で書きたいが, matplotlibはとても不便で使いたくないのでplotnineを使って描いている. 使い方を知らない人は私が昔作った pysocviz が参考になるかもしれない. 計算の重要な部分もPythonではなく C++ になっている.
シミュレーションの実装に関する技術的な説明をする.
次世代の苗字別人口は, 全人口から半分を, 人口比で重み付けした上で無作為非復元抽出したものと同等になるはずだ. よって, 愚直に全人口のランダムな組み合わせを考える必要はない. pandas.DataFrame.sample が一番簡単だが, 私のPCでは1世代の計算だけでも数分かかってしまう. 並列化もできない計算なので ここだけ pybind11 を使用して C++ で書き直した.7
乱数生成について
結局, 私の思いつく方法では超幾何乱数を効率よく計算できなかったため, 同数の無作為非復元抽出から計算する方法を採用した. なるべく計算量を少なくしたつもりだが, 苗字を上位100に限定してもなお, 1世代あたりの計算に10秒以上かかる. ここでは, 乱数生成に関する技術的な補足を述べる.
まず, 超幾何乱数を生成する関数はC++の標準ライブラリにはない. GSLやその他のいくつかのアルゴリズムを見つけたり試したりしていたが, いずれも試行回数が膨大な場合を想定したものではないため, 実際に使用してみると非常に遅く, 1世代ぶんの計算に何十分もかかるものが多かった. 例えばこれが復元抽出であれば, 多項乱数を二項乱数の繰り返しで計算できるため, かなり高速に計算できる. しかし, これが非復元抽出の場合は, 多変量超幾何分布が必要になる. 多変量超幾何分布もまた, 単変量の繰り替えしで求められるが, 今回は有限母集団が1億以上とかなり大きい. この場合は単変量であっても時間がかかる. GSLの実装でも1時間放置しても1世代ぶんすら終わらなかった. 計算の性質のため並列分散処理で速くすることも難しい. 超幾何分布の確率関数を効率よく計算する方法という話も見つけたが, 確率関数を元に逆関数法で乱数を求めるにしても, どうしても1つの乱数を得るたびに膨大な回数のループ処理が必要になる. 結局, 超幾何分布を陽に求めるアプローチは諦めて, 人口と同数のインデックスに対して非復元抽出する処理を採用した. 計算量は であり, 私が思いついた中ではこれが一番速かったが, それでも4000位までの全苗字に対する計算では, 1世代あたりに数分かかり, 全く実用的ではない. 採用した以外の実装も一応残しておいたので, C++が多少わかる人はソースを適当に書き換えて試せるだろう. というか分かる人は改善方法をプルリクマジで歓迎します.
シミュレーションは時間がかかるものの, 終わらないレベルではないので今もやり直している. 有限母集団が非常に大きい場合の(多項)超幾何乱数の高速な生成法か, 現在の私の実装を大幅に高速化する方法を知っている人がいたらマジで教えてください.8
技術的に注意すべきもう1つの点は, 出力データが膨大になるのでストレージの限界が先に来る可能性が高いということである. そのため, 適当な区間で区切ってデータを保存するなど, out-of-core な処理が必要になるが, 今回は分散処理ライブラリなど特に使わず適当に分割する処理を自分で書いている.
ファイルを分割しても合計すると相当なサイズになり, 私のストレージが溢れそうだった9ため, 今回は保存するデータを10000世代に1つ程度に間引きした. 事前の理論分析から, 短期間で大きな変化があるとは考えにくいため, 大きな問題はないだろう. pandasは普通に使っていてもあまり書きやすくなく, かといって大量のデータを処理する際にも工夫が必要になるため, いい加減新しいフレームワークが欲しいのだが, 結局いつも惰性で書いてしまっている.
もう1つ, 気になっている問題があるが, 私はあまり詳しくないので無視していいか自信がない. このシミュレーションでは, 実装方法によっては膨大な数の乱数生成が必要になる. そのため, 今回使用している疑似乱数アルゴリズムである, MT法が理論上保証している多次元一様分布の次元の限界を超えてしまわないか, というのが気になっている.
計算用のプログラムパッケージ化して公開している. Ubuntuなら以下のようにしてインストールできる.
sudo apt install libgsl-dev pip install git+https://github.com/Gedevan-Aleksizde/surname-sim
このパッケージに含まれているのはC++で書いたコアな部分と再現用のデータセットだけなので, 使いやすくするためPythonでラッパーを用意する.
シミュレーションを実行する関数
from surname_sim.sim import SimpleSimulat def simuoation_chunk_hg( df_initial:pd.DataFrame, total_iter:int, chunk_size:int, seed:int, saveto:Path, thinning:bool=True, colname_surname:str='surname', colname_number:str='number', colname_time:str='t', progress_bar:bool=True, drop_extinction:bool=True, early_termination:Optional[int]=1, fname_prefix='rw' )->bool: if early_termination is None: early_termination = 0 total_iter = int(total_iter) chunk_size = int(chunk_size) seed = int(seed) n_chunk = int(total_iter // chunk_size) mod = total_iter % chunk_size n_chunk += (1 if mod > 0 else 0) gen = SimpleSimulator(seed=seed) df_initial = df_initial.loc[lambda d: d[colname_time] == d[colname_time].max()] names = df_initial[colname_surname].values tmp = df_initial[colname_number].values for i in (tqdm(range(n_chunk)) if progress_bar else range(n_chunk)): chunk = gen.iterateChunkHG( tmp, chunk_size if i < n_chunk else mod, thinning ) chunk = pd.DataFrame(chunk, columns=names) if drop_extinction: dropped_col = (chunk.tail(1).values == 0)[0] chunk = chunk.loc[:, ~dropped_col] names = chunk.columns tmp = chunk.values[-1, :] chunk['chunk'] = i chunk['t'] = chunk.index + 1 + i * chunk_size chunk.to_parquet( saveto.joinpath( '{prefix}-{i:0{width}d}.parquet'.format(prefix=fname_prefix, width=len(str(n_chunk)), i=i), ), index=False ) if tmp.shape[0] <= early_termination: print(f'The number of the left surnames is {early_termination}. simulation temirnated at {i}-th chunk (total iteration is {chunk_size * i}/{total_iter})') break return True
OUTPUT_DIR.joinpath('test').mkdir(parents=True, exist_ok=True) simuoation_chunk_hg( df_initial=d_myoji, total_iter=10e8, chunk_size=10e4, seed=SEED, saveto=OUTPUT_DIR.joinpath('test'))
GARCHモデルの結果
計算量が膨大であるため, 100位までの苗字を, 10000回世代交代させた結果だけを計算した. としゅきー氏のシミュレーションでは30年ごとに世代交代すると仮定していたので, およそ3400万回の世代交代で1億年が経過することになるため, それくらいの回数あることが望ましいが, 計算時間もAWSの利用料もかなりかかりそうなので一旦打ち切った. 一方で, 確率の計算を妥協した, やや不正確なシミュレーションであれば, 高速で計算できるため, 次のセクションで何通りも試した結果を提示している.
結果の再現性のため, 乱数のシード値を固定している.10 SEED = 42 の数字を変えると, 違う結末を見られる.
苗字ごとの人口の推移を表すと 図 4 のようになる. 全順位を表示しても読めないので, シミュレーションで最後まで残った順で10種類の苗字だけを強調して表示する.
長大なコード
def make_plot_data( files:Iterable[Path], colname_number:str='number', colname_name:str='surname', max_rank:int=10, verbose:bool=False )->pd.DataFrame: files = list(files) flist = [str(x) for x in files] flist.sort() tmp = [None] * len(flist) for i, fp in enumerate(flist): tmp[i] = ( pd.read_parquet(fp) .drop(columns=['t', 'chunk']) .ffill().iloc[-1] ) tmp = pd.concat(tmp, axis=1).transpose() tmp = ( tmp.ffill().iloc[-1] .reset_index() .rename(columns={'index': 'surname', 0: 'number'}) .sort_values(['number'], ascending=False) ) last10 = ( tmp .head(n=max_rank) .reset_index(drop=True) .assign(rank=lambda d: d.index + 1) .drop(columns=['number']) ) if verbose: print(last10) l = [] for fp in files: if verbose: print(f'reading {fp}') tmp = read_sim_result_as_long(fp).merge(last10, on=colname_name, how='left') tmp[colname_name] = np.where(tmp['rank'].isna(), 'その他', tmp[colname_name]) tmp = tmp.assign( rank=lambda d: np.where(d['rank'].isna(), 11, d['rank']) ).reset_index(drop=True) tmp = tmp.groupby(['t', 'rank']).agg({colname_name: 'first', colname_number: 'sum'}).reset_index() l += [tmp] d_result = pd.concat(l) d_result[colname_name] = pd.Categorical(d_result[colname_name], last10[colname_name].tolist() + ['その他'], ordered=True) return d_result def read_sim_result_as_long(fp:Path)->pd.DataFrame: d = pd.read_parquet(fp) d = ( d .drop(columns=['chunk']) .melt(id_vars='t', var_name='surname', value_name='number') ) return d
def make_diversity_data( files:Iterable[Path], colname_number:str='number', colname_name:str='surname', max_rank:int=10, verbose:bool=False )->pd.DataFrame: files = list(files) flist = [str(x) for x in files] l = [] for fp in files: if verbose: print(f'reading {fp}') tmp = ( read_sim_result_as_long(fp) .loc[lambda d: d['number'] > 0] .groupby('t')['number'].nunique() ).reset_index() l += [tmp] d_result = pd.concat(l) return d_result || >|python| d_result = pd.concat( [ make_plot_data( OUTPUT_DIR.joinpath(f'rwhg100').glob('rw*'), verbose=False ).assign(series=1) ] )
d_result_diversity = pd.concat( [ make_diversity_data( OUTPUT_DIR.joinpath(f'rwhg100').glob('rw-*'), verbose=False ).assign(series=1) ] )
参考に, 現在の苗字別人口上位10を再掲する.
表を出力するコード
d_top10_init = d_myoji.sort_values(['number'], ascending=False).iloc[0:10].rename(columns={'number': 'number_2024'}).drop(columns=['t']) d_top10_ini
| surname | number_2024 | rank |
|---|---|---|
| 佐藤 | 1830000 | 1 |
| 鈴木 | 1769000 | 2 |
| 高橋 | 1383000 | 3 |
| 田中 | 1312000 | 4 |
| 伊藤 | 1053000 | 5 |
| 渡辺 | 1043000 | 6 |
| 山本 | 1029000 | 7 |
| 中村 | 1026000 | 8 |
| 小林 | 1010000 | 9 |
| 加藤 | 873000 | 10 |
結果をグラフに表す. シミュレーションのデータは膨大なので, 結果の数値を10世代ごとに間引きして保存している. 凡例の名前の後の数字は現在の順位を表している.
グラフを描くコード
( ggplot( ( d_result .loc[lambda d: (d['t'] >= 0) & (d['t'] < 3000 * 10e4 )] .drop(columns=['rank']) .merge(d_myoji_full[['surname', 'rank']], on='surname', how='left') .assign( mill=lambda d: d['number']/1000000, t=lambda d: d['t']/10, surname=lambda d: np.where( d['surname'] == 'その他', 'その他', d['surname'] + ' (' + d['rank'].fillna(-1).astype(int).astype(str) +')' ) ) .assign( surname=lambda d: pd.Categorical( d['surname'], d.sort_values(['t', 'rank'])['surname'].unique().tolist() ) ) ), aes(x='t', y='mill', group='surname', fill='surname') ) + geom_area(position='stack', stat='identity') + scale_fill_discrete(name='上位10苗字') + scale_x_continuous(labels=comma_format()) + labs( x='世代 (10世代)', y='人口 (/1,000,000人)', title='1万世代後の苗字別人口の推移', caption='カッコ内の数字は現在の人口順位') + guides(fill=guide_legend(nrow=2, order=1, byrow = True)) + theme(legend_position='bottom') )

多少の順位の変動はあるが, 1万世代の交代を経ても, 佐藤が大半になることはなく, 各苗字別人口のシェアは横ばいに見える.
よって, 暫定的にこう結論づける.
このシミュレーションでは, 特定の苗字の人口が一定率で増加し続けるという, 現実にほぼありえない仮定ではなく, 現在の人口比率に応じて相対的かつランダムにカップルが結婚することで苗字別人口が増減するという, より現実的な仮定のもとでシミュレーションを行った. 現時点では長期間かつ数万の苗字を使ったシミュレーションを行えなかったが, 1万世代後になっても, 人口で上位100に入る苗字はいずれも絶滅することがなかった. よって, 数百年や数千年程度の時間経過で日本の苗字が佐藤のみになる可能性は低いといえる.
シミュレーションの追試
上記のシミュレーションは, 上位100の苗字しか使用していないため, 現実の日本人口とはかなり異なってしまう. しかしながら, 計算リソースの制約により, これ以上高度なシミュレーションは難しい. そこで, 冒頭の仮定とは異なるが, 高速に計算可能なシミュレーションで, 仮説を補強するための傍証を追加しようと思う.
具体的には, 多変量超幾何分布を多項分布で置き換えて計算する. 多項分布と多変量超幾何分布は性質が似ているが, 多項分布は復元抽出であるため, 実現不可能な組み合わせのカップルによる結婚が発生してしまい, 結果として現実に可能な数より大きな人口変動が発生してしまう可能性があるため, シミュレーションとしては不正確である. しかし, 人数の多い苗字のほうが次の世代に残る数も多いという性質は変わらない. 二項分布と超幾何分布を比較すると, 期待値は等しく, 分散は超幾何分布のほうが小さいことを考慮すれば, このシミュレーションで他の全ての苗字の絶滅を見届けることができれば, 正確に超幾何分布で計算した場合と比べ, 苗字の絶滅はもう少し後であろう, という推論くらいはできる. 幸いなことに, 多項分布の計算は超幾何分布よりはるかに高速に計算できるため, 1億世代ぶんのシミュレーションを10回実行した結果をここに示せる.
さきほどの理論分析と同じように, 簡単にモデルの理論的な性質を簡単に確認しておく. 二項分布の期待値は, 超幾何分布と同様で, 現在の苗字別人口と一致し, 何世代後も同じである. 簡単なので式展開は省略する. そして各世代の苗字別人口の分散の対角成分は以下のような再帰式で表せる.
超幾何分布の場合の式を再掲する.
が大きいため, 注目すべきは両式の第2項である. 多項分布で近似した場合の分散の世代ごとの増分は 超幾何分布のおよそ2倍だということになる. よって, 多項分布を使ったシミュレーションでは, 苗字の絶滅速度を過大に見積もることになる.
シミュレーションを実行するコード
def simuoation_rw_mn_chunk( df_initial:pd.DataFrame, total_iter:int, chunk_size:int, seed:int, saveto:Path, thinning:bool=True, colname_surname:str='surname', colname_number:str='number', colname_time:str='t', progress_bar:bool=True, drop_extinction:bool=True, early_termination:Optional[int]=1, fname_prefix='rw' )->bool: if early_termination is None: early_termination = 0 total_iter = int(total_iter) chunk_size = int(chunk_size) seed = int(seed) n_chunk = int(total_iter // chunk_size) mod = total_iter % chunk_size n_chunk += (1 if mod > 0 else 0) gen = SimpleSimulator(seed=seed) df_initial = df_initial.loc[lambda d: d[colname_time] == d[colname_time].max()] names = df_initial[colname_surname].values tmp = df_initial[colname_number].values for i in (tqdm(range(n_chunk)) if progress_bar else range(n_chunk)): chunk = gen.iterateChunkMN( tmp, chunk_size if i < n_chunk else mod, thinning ) chunk = pd.DataFrame(chunk, columns=names) if drop_extinction: dropped_col = (chunk.tail(1).values == 0)[0] chunk = chunk.loc[:, ~dropped_col] names = chunk.columns tmp = chunk.values[-1, :] chunk['chunk'] = i chunk['t'] = chunk.index + 1 + i * chunk_size chunk.to_parquet( saveto.joinpath( '{prefix}-{i:0{width}d}.parquet'.format(prefix=fname_prefix, width=len(str(n_chunk)), i=i), ), index=False ) if tmp.shape[0] <= early_termination: print(f'The number of the left surnames is {early_termination}. simulation temirnated at {i}-th chunk (total iteration is {chunk_size * i}/{total_iter})') break return True
def tmp(s:int)->None: tmp_dir = OUTPUT_DIR.joinpath(f'rwbn{s:03}') if not tmp_dir.exists(): tmp_dir.mkdir(parents=True) print(f'simulating series {s}...') simuoation_rw_mn_chunk( df_initial=d_myoji_full, total_iter=10e8, chunk_size=10e4, seed=SEED + s, saveto=tmp_dir ) with Pool(N_PARALLEL) as p: p.map(tmp, range(1, 11))
出力ファイルを整形するコード
d_result_mn = pd.concat( [ make_plot_data( OUTPUT_DIR.joinpath(f'rwmn{s:03}').glob('rw-*'), verbose=False ).assign(series=s) for s in range(1, 11) ] ) d_result_diversity_mn = pd.concat( [ make_diversity_data( OUTPUT_DIR.joinpath(f'rwmn{s:03}').glob('rw-*'), verbose=False ).assign(series=s) for s in range(1, 11) ] )
異なる乱数で10回シミュレーションを行ったところ, いずれも1千万回程度の世代交代で, 1つの苗字を残して絶滅した. その結果が 図 5 である. どの苗字が生き残るかの予測は困難だが, 分散の大きさは計算可能なので, 絶滅する時期がおおむね1億回程度の世代交代後であることは分かる.
グラフを描くコード
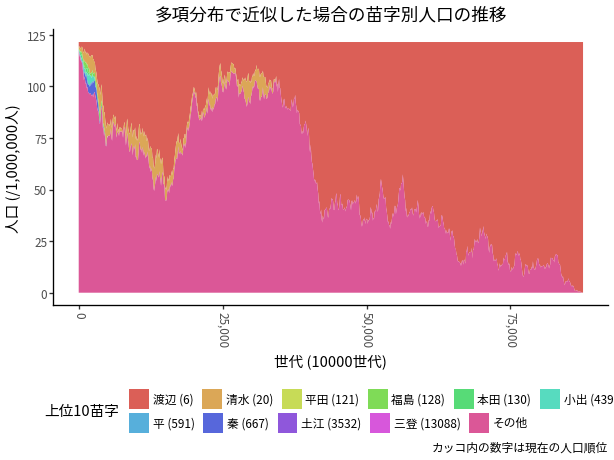
( ggplot( ( d_result_mn .loc[lambda d: (d['t'] >= 0) & (d['t'] < 3000 * 10e4 )] .sort_values(['t', 'rank']) .assign( mill=lambda d: d['number']/1000000, t=lambda d: d['t']/10000 ) ), aes(x='t', y='mill', group='surname', fill='surname') ) + geom_area(position='stack', stat='identity') + scale_fill_discrete(name='上位10苗字') + scale_x_continuous(labels=comma_format()) + labs(x='世代 (10000世代)', y='人口 (/1,000,000人)', title='多項分布で近似した場合の苗字別人口の推移') + facet_wrap('~series') + theme(legend_position='none', axis_text_x=element_text(angle=-90)) )

これらのうちの1系列だけを取り出すと, 図 6 のようになる. 最初の数万世代のうちに渡辺一強となり, 清水がしばらくしぶとく残りづづけるが, 8000万世代後くらいに絶滅し, 渡辺だけが生き残る.
グラフを描くコード
( ggplot( ( d_result_mn .loc[lambda d: d['series'] == 1] .loc[lambda d: (d['t'] >= 0) & (d['t'] < 3000 * 10e4 )] .drop(columns=['rank']) .merge(d_myoji_full[['surname', 'rank']], on='surname', how='left') .assign( mill=lambda d: d['number']/1000000, t=lambda d: d['t']/1000, surname=lambda d: np.where( d['surname'] == 'その他', 'その他', d['surname'] + ' (' + d['rank'].fillna(-1).astype(int).astype(str) +')' ) ) .assign( surname=lambda d: pd.Categorical( d['surname'], d.sort_values(['t', 'rank'])['surname'].unique().tolist() ) ) ), aes(x='t', y='mill', group='surname', fill='surname') ) + geom_area(position='stack', stat='identity') + scale_fill_discrete(name='上位10苗字') + scale_x_continuous(labels=comma_format()) + labs( x='世代 (10000世代)', y='人口 (/1,000,000人)', title='多項分布で近似した場合の苗字別人口の推移', caption='カッコ内の数字は現在の人口順位') + guides(fill=guide_legend(nrow=2, order=1, byrow = True)) + theme(legend_position='bottom', axis_text_x=element_text(angle=-90)) )
なお, 10回の異なるシミュレーション結果でそれぞれ生き残った苗字は, このようになった. generations は苗字が1つを残して絶滅するまでの世代交代の回数で, rank は現在の人口順である. それぞれ結果はばらばらで, 「宝蔵寺」「濱端」など, 現在はとてもマイナーな苗字が生き残る場合もある.
表を描くコード
( d_result_mn .sort_values(['series', 't']) .groupby('series') .last()[['t', 'surname']] .reset_index() .merge(d_myoji_full[['surname', 'rank']], on='surname') .rename(columns={'t': 'generations'}) )
| series | generations | surname | rank |
|---|---|---|---|
| 1 | 87600001 | 渡辺 | 6 |
| 2 | 102000001 | 宝蔵寺 | 13850 |
| 3 | 172200001 | 濱端 | 21652 |
| 4 | 74000001 | 生田 | 741 |
| 5 | 84700001 | 内田 | 63 |
| 6 | 108200001 | 藤木 | 683 |
| 7 | 117800001 | 臼杵 | 3040 |
| 8 | 86400001 | 田中 | 4 |
| 9 | 109100001 | 大島 | 169 |
| 10 | 116200001 | 重村 | 2826 |
次に, 苗字の多様性の減少をグラフにする.
グラフを描くコード
( ggplot( ( d_result_diversity_mn .assign( series=lambda d: d['series'].astype(str), t = lambda d: d['t']/10000 ) ), aes(x='t', y='number', group='series', color='series') ) + geom_line() + labs(x='世代(10000世代)', y='苗字の種類数', title='苗字の多様性の推移') + theme(legend_position='none') )

かなり極端なグラフとなった. 多項分布を使ったシミュレーションでは, 1万世代後には苗字が800種類程度にまで減少し, さらに5千万世代後までには10種類未満になる可能性が高いという結果となった. 図 7 を対数表記にしたものが 図 8 となる.
グラフを描くコード
( ggplot( ( d_result_diversity_mn .assign( series=lambda d: d['series'].astype(str), t = lambda d: d['t']/10000 ) ), aes(x='t', y='number', group='series', color='series') ) + geom_line() + scale_y_log10() + labs(x='世代(10000世代)', y='苗字の種類数 (対数)', title='苗字の多様性の推移 (対数表示)') + theme(legend_position='none') )

多項分布による簡易的なシミュレーションの結果, 事前の理論分析に基づく予想通りの結果となった. つまり, 以下の事実が確認できた.
- 生き残る苗字は毎回異なる
- 現在は人口の少ない苗字が生き残ることがある
実際の減少速度に注目すると, 1万世代後までには4万種類あった苗字が1000種類未満まで減少し, その後さらに数千万世代を経て1つの苗字に収束する. 理論上減少が速くなる多項分布でこの程度の速度であるなら, 実際の減少速度はこれの何倍も遅いだろう. よって, 少なくとも今後1万年以内に苗字が佐藤だけになる可能性は低いという結果がここでも得られた. これは個人的な感想だが, 苗字や姓や氏族という概念はたかだか数千年そこら程度の歴史しかないことを考えると, 思いの外長続きしていると思う. (日本に至っては, 国民の多くが苗字を持つようになって200年も経っていない.)
より複雑なシミュレーションについて
シミュレーションは単純化して考えられるのが利点である. それが非現実的であったとしても, どういう仮定がどういう結末を引き起こすがの議論ができる. 今回のような遠い未来を予想するシミュレーションは, 暗黙の前提がいくつも存在する. 今後1億年以内にコロナウイルスよりも恐ろしい致死性のウイルスが大流行して人類が絶滅する可能性も考慮していないし, 全人類が不老不死になり子孫を残さなくなる可能性も考慮していない. こういった環境そのものを変化させる事件が起こることで結果が変わる可能性はいくらでもあるため, あらゆる観点で「現実的な」シミュレーションを実施することは根本的に不可能である. そのため, 一部を切り取って仮定が非現実的であるとか, 計算が単純すぎるといった点だけで批判するのはナンセンスである. 仮定と結論のつながりが適切でないとか, 疑問に対して不適切な仮定を立てて都合の良い結果を導いていることを指摘することこそが, 建設的な批判というものだろう.
これに関連して, 国立社会保障・人口問題研究所が2012年に行った日本の将来推計人口の報告書の『解説および参考推計報告書』の序文の一節が含蓄のある文章だと思ったので引用する.
人口変動を含め、社会科学が対象とする事象について「予測」を行うということは、未来を言い当てるという種類の予測、すなわち予報 (forecast) をするということとは異なる。天体の起動や天候などと違って、社会経済は人間が変えていくものであるから、我々の今後の行動しだいで無数の展開の可能性を持っており、現在において定まった未来というものは存在しない。したがって、科学的にそれを言い当てる行為もあり得ないだろう。すなわち、将来の社会経済を予測するということは、標本データから母集団の未知の平均値を推定するといった作業とは本質的に異なるものである。すなわり、推定すべき真の値はわからないのではなく、(まだ) 存在しないのである。
(中略)
たがって、一般に社会科学における科学的予測とは、結果として将来を言い当てることに役割があるのではなく、科学的妥当性のある前提の下に、今後に何が起こり得るかを示すことを目的としている。将来人口推計についても同様であり、人口動態自称 (出生、死亡、ならびに人口移動) の現在までの趨勢を前提として、それが帰結する人口の姿を提示することを役割としている。
(中略)実際の人口推移が明らかとなったときに、仮にそれが将来推計人口と異なる動きを見せ始めたとすると、それは前提に含まれない新たな変化か、あるいは趨勢の加速、また減速といった状況変化が存在することを示している。こうした変化をいちはやく見出すことも、実は将来推計人口の重要な役割の一つである。
これはシミュレーションの価値を的確に言い表した言葉だと私は思う. 統計的推測とは「根本的に異なる」という主張には私は同意しないが, 社会現象を遠い将来まで予測することは技術的にとても難しいのは事実だ. 技術的困難さに対する妥協として, シミュレーションが「非現実的な」側面を持ってしまうことはあるが, 一方で現実とは異なる想定をすることで何が起こるのか, という思考実験を精巧に行う能力もある.11 今回の話題の根本的な問である, 夫婦同姓である現状に対し, もし夫婦別姓であったらどうなるか, という問いかけも, シミュレーションに向いた題材である.
とはいえ, 現実世界の未来をより高い確度で予想したいというのは, 多くの人間に共通する欲求でもある. 最後に, 今回のシミュレーションをさらに「現実的な」状況に近づけるために, 私が考えたアイディアをいくつか紹介する. 「佐藤以外絶滅した日本」という未来がどれくらい現実味があることなのかの検証のために, これらも試してみたいところだが, 現状は計算に時間がかかりすぎる問題があるため, 答えが出るのは当分先である. せめて現在の1000倍くらい速く計算できなければ, 実用的ではない.
なので現在のプログラムを改良するPRやAWSの利用料カンパをお待ちしています.
既に紹介したシミュレーションで, 特に現実的でないと思う箇所をいくつか挙げる.
- 全員が結婚する想定になっている
- 兄弟姉妹でも結婚している可能性がある
- 同世代どうしの結婚しか発生していない, あるいは幼児も老人も含め全ての世代が結婚し出産している
- 子どもの数が固定されており, 実際の日本社会で発生している少子化が起こらず, 未来永劫人口が一定になっている. 奇数だと1件減るが些細なことだろう.
- 新しい苗字が作られることがない
(a, d) は修正が比較的簡単である. 例えば, 現在の結婚率と合計特殊出生数の水準が将来も続くと仮定して, 人口全体で結婚する人間を一部に限定したり, 子どもの数を調整したりすると, より現実の推移に近づくかもしれない. (b) は, 完全にランダムということは, 兄弟姉妹どうしでも結婚している社会のシミュレーションをしている可能性がある, という指摘である. 個人的には, 計算が複雑になるわりに結果に大きく影響しなさそうだと予想しているが, 関心がある人は多そうなので試してみてもよさそうだ.
は, 現実に必ず同年齢の人間が結婚するとは限らず, 世代交代はそれぞれ重複しているという指摘である. しかし, 年齢を考慮してペアリングをするような計算をしても, あまり意味がなさそうだと個人的に予想している. 結婚年齢は出生数には影響すると思われるが, 苗字の選択に影響するとは思えない. シミュレーションには出生数だけ分かっていれば十分だ. だが一方で, この設定は幼児も老人も関係なく結婚している, と仮定しているとも取れる. 幼年期・成人期 (結婚・出産可能年齢)・老齢期, の3世代におおまかにわけてシミュレーションすることで, 苗字別人口シェアのダイナミクスに変化があるかもしれない.
も, わざわざ, より「現実的」なものを求めるメリットが少なそうな問題だ. 日本では「止むをえない事由」で苗字を改名する手続きがある. 外国人が帰化する際も, 自由に創作できる事が多いようだ. 年間で何件くらいこのような苗字の変更が発生しているのか, 政府資料では公開されていないようだが, この手続きで改名する人間はごくわずかだろう. だが, 既に行ったシミュレーションでは多数派の苗字が絶滅する可能性も十分あるとわかっている. 日本人が創作苗字だらけになる未来のシミュレーションも面白そうである. あるいは, 海外のように複合姓にしたらどうなるか, というのも面白いかもしれない.
男女別
(a, d) の問題は, 比較的簡単な変更で結果を得られるかもしれない.
世代重複
当初のシミュレーションでは, 世代交代ごとに人口の全てが結婚している. しかし, 現実にはそんなことは起こり得ないため, 現実的な世代交代よりも速く苗字別人口の推移が起こると予想できる. 例えばとしゅきー氏のシミュレーションでは30年ごとに1世代交代すると仮定して, 他の苗字が絶滅するまでの年数を計算しているが, 今回試したGARCHモデルのような全員が同時に結婚するモデルでは, 苗字絶滅までの世代交代数を年数に正確に変換できないだろう. そのため, 結婚可能年齢を考慮する必要がある.
- 3世代の合計を総人口とする. つまり, これまで結婚するとして計算していた世代は再生産年齢人口で, 1世代後は幼年人口, 1世代前は老齢人口である.
理論上はもっと細かく区切っても良いだろう. 人口推計では5歳毎に区切った年齢別人口を計算することが多い.
創作苗字
- の問題を解消するために, 世代ごとに一定の割合でランダムに新しい姓を発生させる. 実際の発生件数は不明なので, いくつか適当な候補を用意して計算する
三親等の婚姻禁止ルール
このシミュレーションを見た時, 似たような話をどっかで聞いたなと思ったので適当に検索してみたら見つかった. 日本の法律では三親等内での婚姻が認められない. この制約を設ければ, 苗字の絶滅問題に対してかなり現実的な予想ができそうな気がしている.
https://kiito.hatenablog.com/entry/2014/12/15/003648
しかし, このシミュレーションを日本の苗字別人口に当てはめるのはかなり難易度が高そうだ. 一人ひとりの両親と先祖の情報まで参照する必要がある上に, 苗字と実際の血縁関係を紐付ける情報がない. 実証用のデータも, 計算の技術的難度も高い.
より高度な人口学的モデル
マイナーな姓というのは特定の地域に固まって見られる傾向がある. 人間の住居の移動にもコストがかかるからだ. そういった社会の実際の制約を反映したモデルを作れば, より実現可能性の高い結果も導けるだろう. これは地域別人口推計という, まさに人口学の専門家が取り組んでいる主要な問題の1つだ. 私も以前ちょっとだけ真似したことがある. だが実際の人口推計に使われているようなモデルを苗字シミュレーションに転用するのは大変なので今回はここまでにする.
結論
今回は夫婦同姓による苗字の多様性減少という問題について, 現在の日本の苗字別人口を反映した人間たちが, ランダムに結婚し子孫を残するという, 単純なシミュレーションを行って検証した. 計算資源の制約で, 実際の日本の苗字別人口から大幅にスケールダウンした結果しか得られなかったが, 少なくとも事前の理論分析に基づく予想を裏付ける結果を得られた. その結果とは, 冒頭の東北大高齢経済社会研究センターによる試算とは大きく異なるもので, 特に大きな違いは以下の3点である.
- 夫婦同姓であってもなくても, 遠い未来に1つの苗字以外が絶滅する可能性がある. そして, 唯一生き残る苗字が佐藤であるとは限らない.
- 夫婦同姓を続けた場合でも, 他の苗字が絶滅するタイミングは不確定である.
- 他の苗字が絶滅し, 日本人の苗字が1つしか残らなくなる時期は, 早くとも数千万世代後というスケールであり, たかだか数百年や数千年という「短期間」で苗字が絶滅する可能性は低い.
この結果の違いは, 高齢経済社会研究センターの試算の根拠となる, 佐藤姓の増加率のみが一定であるという仮定は現実にはほとんどありえないという問題を指摘した上で, 日本人の結婚活動としてより現実的な仮定に基づいて改善したシミュレーションにより判明したものであり, より実現可能性の高い結果だと言える.
しかし, 当初想定していたシミュレーションは, 計算資源の制約のため, 予定通りに行えなかった. 仮定を増やしてより詳細に分析することもできなかったため, 既に紹介したとしゅきー氏のシミュレーションと比べて, ソースコードや理論的背景を明確にできた程度にとどまってしまった. この問題をなんとかして解決したいが, まだ解決の糸口が見つかっていない.
私ごときの素人で検証可能なのはここまでである. 大学の研究機関であれば, スーパーコンピューターなどへのアクセスも容易であろう. ぜひ, より精緻な試算で得られた知見を公開していただきたいと願う.
大湾先生の指摘は, 佐藤姓の増加とともに増加率が減るだろうと予想しているように取れる. これは書き間違えか, あるいは何か別のメカニズムを念頭に置いた発言なのかはわからない.↩︎
元の投稿では, 世代交代が30年周期で発生すると仮定している↩︎
簡単のため, 現在の人口は偶数であると仮定している.↩︎
苗字別人口というベクトルを扱っているので, 分散共分散行列になる. だが長ったらしいため, 単に分散と呼ぶことにする.↩︎
総人口を固定している仮定は, 上記のギブスサンプリング的なシミュレーションに簡略化するためのものであり, 現実に即していない. そのため, 分枝過程をベースに考えたほうがより蓋然性のある結果が導けるだろう.
↩︎意味のない二次配布はしたくないが, 商用利用でなく, クレジットを付けるという条件でなら使用して良い, と書いてあるため, 今回のシミュレーション結果を再現しやすいよう, csvファイルにして用意している.↩︎
他にも試してうまくいかなかった方法を書き残しておく. numba のJITコンパイルでは sample メソッドを高速化できなかった, pypy に切り替えてもさほど速くならなかった. numbpy の乱数メソッドは次元に制約がありそのまま置き換えることができなかった. Cython よりPybind11でそのままC++で書いたほうが手っ取り早いと思って今回はPybind11を使ってみたが, 結局makefileとsetup.pyの両方を自分で書く必要があったので思ったほど便利ではなかった.↩︎
としゅきー氏は4万苗字全てで計算したと書いているが, どうやったのだろうか?もっとスマートなやり方に気づいたのか, ひたすら待ったのか…?↩︎
1世代でも4万次元となるため, 長期間のシミュレーションは簡単にストレージの容量を超えてしまうだろう. 加えて, 古いファイルシステムを使っている場合はファイルサイズの上限や保存できるファイル数の上限を超える可能性もある.↩︎
適当に作ったのでアーキテクチャによっては違う結果になるかもしれない. 一部の乱数用の分布関数はプラットフォームごとに挙動が違うことがあるらしい. 私はUbuntu OSとintelのCPUを使っている.↩︎
実際に, 過去に将来推計人口が発表された際には, 物申すのが好きな人間たちがこういった意図を理解せずに「出生率がこんなに大きく回復するわけがない, でたらめな予測だ」といった的はずれな批判を行ったり, より最近ではコロナウイルスの感染規模に関するシミュレーションに関しても, 予測, あるいは当てはまりの良いモデルが求められている場面と, そうでない場面の違いをよく理解せずに論じている人が散見されたのは残念である.↩︎