2016/12/15: にわかに閲覧者が増えたのでおかしなところを微修正
概要
統計学史をちょっと調べていておもしろかったのでまとめてみた
技術的にはすごく初歩的な話なので, 回帰分析 (最小二乗法) の入門的な「読み物」という位置づけになりそう
入門的な読み物なので, 特に最小二乗法の説明箇所は中学高校の数学の知識だけで理解できるような表現をしている, したつもり.
PDF換算で 10 ページ (ただし画像が結構多い)
惑星の軌道を予測する
連立方程式で惑星の軌道を予測する
19世紀初頭にフランスの数学者ルジャンドル*1が最小二乗法のアイディアを最初に発表したが, ドイツの数学者ガウス*2が直後に自分こそが先に思いついたと主張し, 論争を生んだという (Abdulle & Wanner, 2002, 200 Years of Least Squares Method). しかし, いずれが先かはともかく, その後に最小二乗法を発展させたのは多くはガウスの研究成果である. そこで, ガウスの研究をなぞるようにして最小二乗法を説明する.
ガウスは惑星の軌道を予測する計算方法を考えていた. 仮に惑星が直線上を動くとすると,
という1次式で表現できる. この切片と傾きは, 実際の惑星の位置を2回測定すればいい. 2点の座標を ,
とすると (図1), この2点を通る直線の切片と傾きを求める問題になる.
図1: 2点を通る直線の切片と傾きを求める
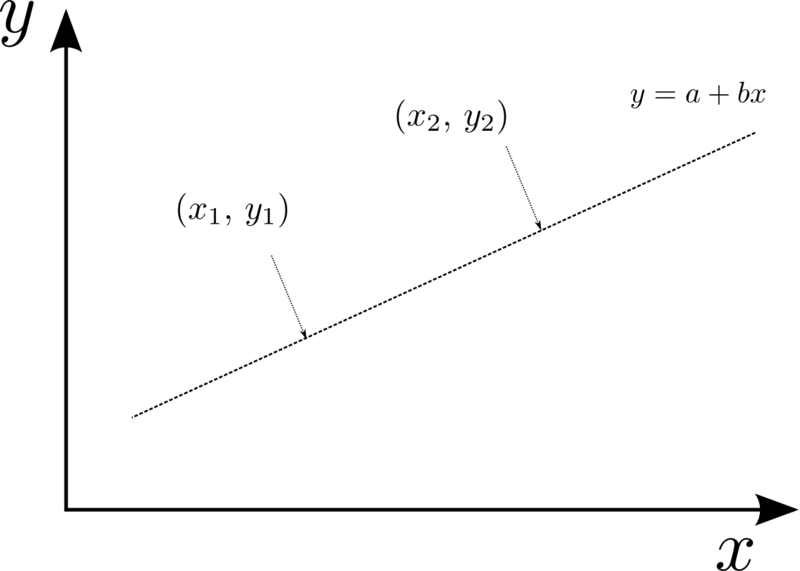
つまり, ,
が未知数の連立方程式という, 中学数学の問題になる. 連立方程式を解くには, 未知数と同じ数だけ方程式があればよい (これもガウスの発見である) し, 確実に答えを求める方法もある (ガウス消去法). これも中学数学の内容の復習だが,
平面 (
平面ではない) に表すならこれは2直線の交点を求める問題と同じである (図2).
図2: 2直線の交点

この1次式の切片と傾きがわかれば, 惑星のこれからの先の動きも予測できるはずである.
ところで, 連立方程式の本数がもう1本増えた場合, どうなるだろうか? 3つ目の点 も同じ直線を通るはずだから,
の答えも変わらない. 変形すれば結局, 最初の2つの式のうちのいずれか1つと同じになるため, 結局2本の連立方程式を解いているのと変わらないからだ (図3).
図3: 3本以上でも結局一点に交わる
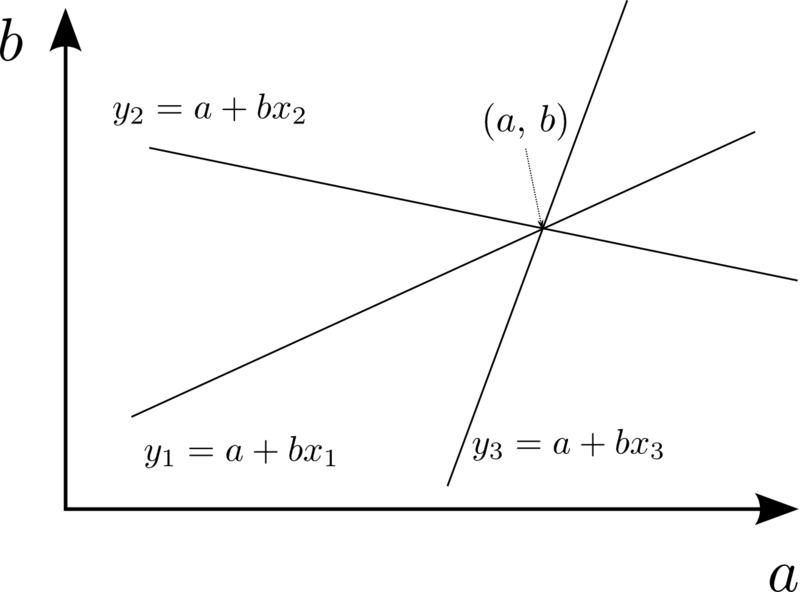
しかし, 実際に3点以上の観測結果から連立方程式を作り解いてみても, 答えがあわないのだ. その理由は誤差である. どうしても星の位置の測定に誤差が生じるのである. つまり, 実際の直線からわずかに外れた点をもとに連立方程式を作成するため, 解が一致しないのである (図4).
ガウス自らが発見した定理からもわかるように, 未知数よりも本数の多い連立方程式からは答えを得ることはできない.
図4: 3直線が一点に交わらない

ガウスがこの問題を解決するために考案したのが最小二乗法である. ガウスのアイディアはこうである. 測定にどうしても誤差が現れるのなら, 連立方程式を解くのは諦め, せめてこの誤差が最も小さくなるようにしつつ, 未知数 ,
を決定しよう, というものである.
図5: 誤差のある観測点
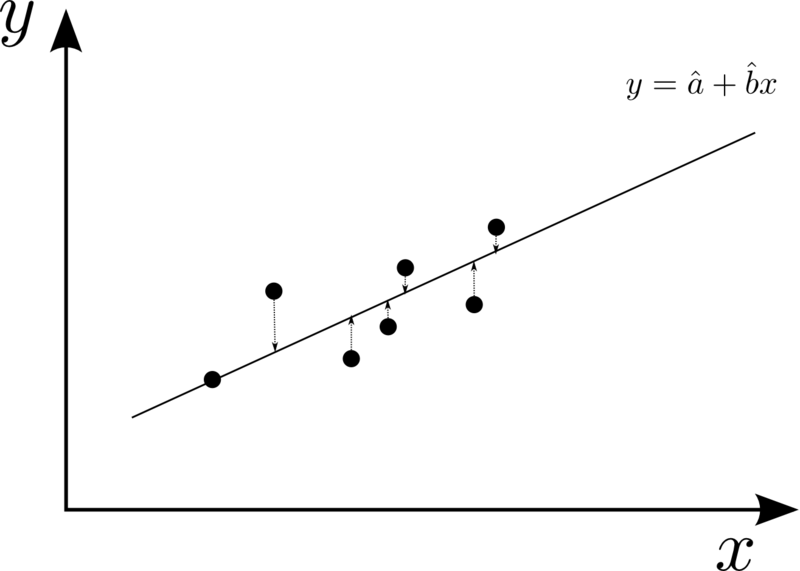
まず, 当初の1次式 は, 誤差がないときの理想的な直線だと考える. これと別に, 誤差があることを認めた現実的な直線として
を考える. は
と一致しているのが理想だが, 今は誤差があるため必ずしも一致しない. そこで, 実際に観測された値
と,
の差が誤差となる . つまり, 誤差は
である. 模式図が図5 である. 観測点が必ずしも直線上にならんでいないため, 「だいたい真ん中を通るように」言い換えると「全体の誤差が小さくなるように」直線を引きたい. しかし, 見た目から適当に線を引いただけでは数学とは言えない. そこで線のひきかたの厳密なルールを考える. 観測した点ごとに誤差があるので, この合計値が「全体の誤差」になる. ただし, ここで単純に合計してはならない. なぜなら, 誤差はプラスマイナスどちらの可能性もあるので, そのまま足しただけだと誤差どうしが打ち消し合ってしまう. 図5の例なら, 直線の上側の観測点の誤差がプラス, 下側の観測点の誤差がマイナスになる. よって, 各点の誤差を2乗したものの合計を, 全体の誤差とすることにした*3.
ここで, 観測点が 3点ではなく, 個の点として書いている. しかし, 単に足しているだけなので, 3点でも
点でも同じだ. これを「全体の誤差」とし, 全体の誤差が最も小さくなるように
,
を決めるのが最小二乗法である. 最小化するには, 高校数学の2次関数を思い出して欲しい.
という関数は, なら必ず下に凸な放物線になる. よって, 最小値が存在する. 先ほどの「全体の誤差」も
,
を変数としてみると, 2次関数とみなせる. 係数はそれぞれ
と
とどちらも正なので, 必ず最小値を持つ. そして, これは高校数学の後半の知識になるが, 最小値を取るときは微分して得られる導関数がゼロになる. よって,
,
でそれぞれで微分してイコールゼロとした方程式ができる.
で微分した場合,
で微分した場合,
という方程式が得られる. があるのでわかりづらいかもしれないが,
は実際に観測する際に具体的な数字が入るし,
,
は未知の定数なので
で
個の和をとっても単に
,
になるだけである (実際に観測したのなら, 観測した点の数の
も分かっているはずだ.). よって, この式を整理すると,
と
に対する2本の連立方程式になる. 2つの未知数に対して2本の方程式があるので, 答えは必ず得られる. 当初の連立方程式では答えを得られなかったが, 答えを必ず得られるように「正規化」するため, この連立方程式は「正規方程式」と呼ばれる.
非線形への発展
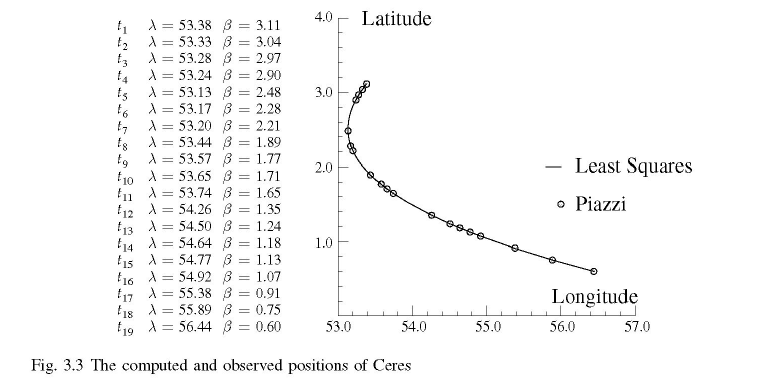
さて, これで直線の軌道を予測できるようになったが, 実際には惑星の軌道は直線ではない. 当時知られていた惑星軌道の法則はケプラー*4の法則であり, それによれば軌道は楕円になる. そこでガウスは, 楕円の式でも同じようにいくつかの観測点から誤差を最小化しつつ係数を求めることはできないかと考え, 「非線形最小二乗法」を考案した. しかし, 非線形最小二乗法は通常の最小二乗法より複雑で, 正規方程式を求めることはできない. そこで彼は, ガウス=ニュートン法と呼ばれる計算方法を考えた. これは, 数列の漸化式のように, 値を代入して次の値を求めることを繰り返せば, 最終的に係数が分かるというものである. これを用いてガウスは準惑星ケレスの軌道を計算した*5. ケレスはピアッツィ*6が 1801年1月1日に発見したが, ピアッツィの体調不良, 悪天候そしてケレスが太陽に接近したため2月12日以降観測できなくなっていた. ピアッツィの観測結果は同年9月にフォン・ツァッハ男爵*7が編集する科学誌 “Monatliche Correspondenz zur Beförderung der Erd- und Himmels-Kunde” に掲載され(図6), ここでケレスの観測問題が提起された. そこでガウスは過去の観測実績から非線形最小二乗法を用いて軌道を予測した論文を同月29日に発表し(図7), その後12月7日にケレスが予測された軌道上に存在することがフォン・ツァッハ男爵によって発見された.
図6: ピアッツィによるケレスの観測記録 (Abdulle and Wanner, 2002 より)
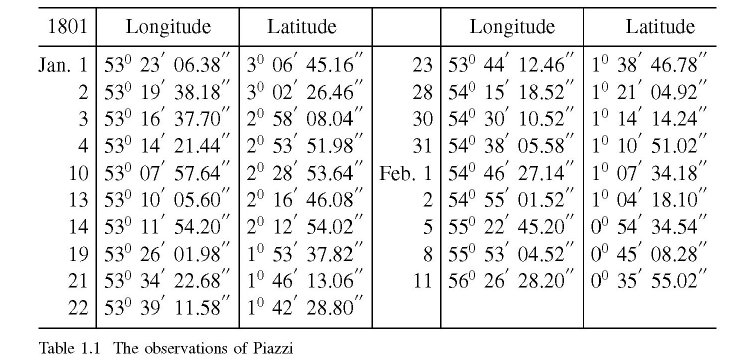
図7: 最小二乗法で当てはめたケレスの軌道 (Abdulle and Wanner, 2002 より)
ものすごく蛇足になるが, 昔, 後輩に最小二乗法がなんなのかを説明するとき, 連立方程式で直線の傾きを求める問題の類推から説明を始めれば, 数学的に高度な知識も要らず抽象的な概念を飲み込みやすいのでは, と考えて解説ノートを作ったことがあった. 今, 最小二乗法の成立の経緯を調べるとじっさいにガウスも連立方程式の拡張のような考え方をして最小二乗法を思いついたらしいので驚いている. もちろん, 数学的に精緻化させたガウスに遅れること200年で, ようやく曖昧なアイディアを出しただけなのだが.
ルジャンドルとの論争
ガウスは当初, 最小二乗法と非線形最小二乗法の具体的な計算方法を公表したがらなかった. しかしルジャンドルが 1805年に “Nouvelles méthodes pour la détermination des orbites des comètes (彗星の軌道決定のための新方法)” で先に最小二乗法を発表すると, ガウスは1809年に “Theoria motus corporum celestium (天体の運行に関する理論)” において最小二乗法の原理は自分が1975年*8の時点で発見していたと主張した (ガウス, 1981, 誤差論)*9. また, ここで誤差の「2乗」を使うことがなぜ妥当かということも説明している. その後, どちらが最初に最小二乗法を発見したかで2人は書簡を通じて論争した. 論争は結局解決しなかったが, ガウスは誤差を最小化する問題に対して優れていることを証明する発展的な研究を次々と発表した.
たとえば, 彼自身が研究していた正規分布 (この当時はガウス分布と呼ばれていた. ガウスがその性質を研究していたからである) と誤差を関連させた. 1809年にラプラス*10が中心極限定理を発見した. 多くの点で観測した場合, 誤差が正規分布で表せるのだ. 正規分布の性質から, 最小二乗法で計算した予測式は誤差が平均してゼロになる. よって最小二乗法が軌道予測以外の場面でも幅広く応用できる可能性を示したことになる.
もう1つの重要な発見は, 1823年に “Theoria combinationis observationum erronibus minimis obnoxiae” で発表されたもので, ガウス=マルコフ定理と呼ばれる定理である. 誤差のある観察データから1次式の係数を計算するときに, 最小二乗法以外の方法も考えられる. 例えば誤差の2乗ではなく絶対値にするという方法もあるし, 「当てずっぽうで決める」というのも方法の1つである. しかし, いずれの方法にせよ, この計算して得られた係数は本当の値との間に誤差がある. ガウス=マルコフ定理は, この誤差 (統計学の用語で言うなら, 正しくは分散) には最小値があり, 最小二乗法なら最小の分散になるように計算できることを保証するものである.
統計学の手法として生まれ変わる最小二乗法
「回帰分析」という言葉の誕生
現在使われている回帰分析 (regression analysis) と言う言葉を最初に使ったのはゴルトン*11で, 生物学者だった彼は軌道ではなく生物が個体ごとに身長や体重に差があるのはなぜか, ということに関心を持った. 生物の身長のデータはたいていベル型の曲線, つまり正規分布を描く. 彼は以下のような式に最小二乗法を適用した.
このとき, たとえば親が平均値から外れた高身長・低身長でも, 子どもはより平均値に近い身長になる傾向を発見した. さらにゴルトンは身長以外の特徴や, 人間以外の生物についても親世代と子世代の特徴を比較し, 同様の傾向があることを発見した. この現象をゴルトンは「平均への回帰」と呼び, 「生物は世代を重ねる毎にみな平均的な形質になる」と考えた.
ガウス以降, 観察データのばらつきは観察時の誤差によるものだと考えられていた. しかし人間の身長が個人で異なるのは明らかに観察の誤差では説明できず, なぜかという問題はずっと議論されてきた. ゴルトンの研究による重要な転換点は, 確率分布を導入してこの問題を説明したこと, そして相関係数という分析の切り口をもたらしたことにある. この研究以降, 最小二乗法を応用して2つの変数の関係を分析することを「回帰分析」と呼ぶようになった. ガウスが最小二乗法を開発した当初の目的は誤差を最小化した回帰式に基づいての予測値を計算することだったが, ここでは係数の値にむしろ関心が映っている. 係数
はいわば2変数の相関係数*12の大きさを表し,さらに十分な根拠があるなら, これは右辺の
の変化によって左辺
が
だけ変化するという「因果効果」を表すと解釈できる .
仮説検定と最小二乗法
ガウスの研究からおよそ1世紀後, 確率分布を用いて厳密に理論化する「数理統計学」の基礎を確立したフィッシャーによって, 最小二乗法は統計学の手法としての地位も得る. 数理統計学のなかでも統計推測 (statistical inference) と呼ばれるものは, 統計学の一分野で, ピアソン*13やフィッシャー*14らによって20世紀初頭に基礎が作られた. それ以前の統計学というのは, 漠然と数字を集計するものだったが, 彼らは確率論に基づいて, その結果が「何%の確率で正しいか」を判定する数々の方法を考案し, これが現在の統計学の基礎になった. ピアソンは, 1900年に最小二乗法の当てはまりに対する仮説検定, 通称「ピアソンのカイ二乗検定」を考案した.
仮説検定とはなにか, ということも説明すると非常に長くなるので, 次のような簡単な説明だけにしておく: 誤差が確率で決まるとすると, 結果が正しいかどうかも確率に左右される. よって, 「Aである」「Bではない」と断定することができない. そこで, 「何%の確率でAである」と予報するのだ. ここで, 確率が50%であればほとんど意味がないが, 「95%の確率でAである」とか「5%の確率でBではない」とか言うことができれば, 100%確実ではないもののかなり信頼できる. ピアソンのカイ二乗検定は「何%の確率で正しい式になっている」かどうかを判定するテストということになる.
一方フィッシャーもスチューデント (ゴセット*15 ) が考案した t-分布 (Student, 1908, The Probable Error of a Mean) を利用して, 最小二乗法で求めた係数 ,
に対して個別に仮説検定を行う, t- 検定を提案した. t-分布は, 正規分布に比べて観測点が少ない場合でも有効な分布である (中心極限定理は観測点が十分多い時に正規分布になるという定理だが, 実際には必ずしも十分な観測ができるわけではない). フィッシャーは, 「誤差が正規分布すると仮定すれば, 係数が t-分布となる」ことを示し, この t-分布を用いて, 「何%の確率で係数がある値と同じか」というテストができることを唱えた (Fisher, 1922, The Goodness of Fit of Regression Formulae and the Distribution of Regression Coefficients). たいていは, 「係数がゼロかどうか」という判定に使われる. たとえばもし「95%の確率で傾き
はゼロ」という結果が出れば, 計算した係数は意味がない可能性が高い. t-検定は 「比較的, 観測点の数が少なくてもできる」というのも重要である.
これが現在の統計学の教科書でよく教えられている, 最小二乗法を用いた回帰分析である.
参考文献
- Abdulle, A., & Wanner, G. (2002). 200 Years of Least Squares Method. Elemente Der Mathematik, 57(2), 45–60.
- Fisher, R. A. (1922). The Goodness of Fit of Regression Formulae and the Distribution of Regression Coefficients. Journal of the Royal Statistical Society, 85, 597–612. doi:http://dx.doi.org/10.1073/pnas.12.12.773-b
- Student. (1908). The Probable Error of a Mean. Biometrika, 6(1), 1–25. doi:http://dx.doi.org/10.2307/2331554
- カール・F. ガウス (1981). 誤差論. 紀伊國屋書店. 飛田武幸・石川耕春訳.

- 作者:カール・F. ガウス
- 出版社/メーカー: 紀伊國屋書店
- 発売日: 1981/05/01
- メディア: 単行本
*1:Adrien-Marie Legendre (1752 – 1833)
*2:Carl Friedrich Gauß (1777 – 1855)
*3:2点間の距離をとるときに2乗してルートをとっていたことを思い出すと良い. 厳密には誤差は距離ではないが, よく似た状況である. また, 誤差の絶対値をとる, という方法を思いつく人もいるかもしれないが, 絶対値を取る場合, この後の計算が非常に面倒になる. コンピュータのない19世紀初頭にこの計算を全て手作業で行うのは酷だろう. とはいえ, 逆に言えば現在はコンピュータがあるため, 2乗ではなく絶対値で計算する方法も実現性があるとして研究されている. なお, ラプラスは最小二乗法の考案より前に絶対値を用いた「最小一乗法」を考案している.
*4:Johannes Kepler (1571 – 1630)
*5:当初は普通の最小二乗法で計算したが, 精度向上のため改良を重ねる過程で非線形最小二乗法を考案した
*6:Giuseppe Piazzi (1746 – 1826)
*7:Franz Xaver Freiherr von Zach (1754 – 1832)
*9:原著は読めないため, 邦訳のクレジットを表記した
*10:Pierre-Simon Laplace (1749 – 1827)
*11:Francis Galton (1822 – 1911)
*13:Karl Pearson (1857 – 1936)
*14:Ronald Aylmer Fisher (1890 – 1962)
*15:William Sealy Gosset (1876 – 1937). 彼は当時 Student というペンネームで論文を発表していた