ill-identified diary

所属組織の見解などとは一切関係なく小難しい話しかしません

トップ > 統計学 > [stan] [R] ベクトル ARIMA (VARIMA) で人口予測 (?)

[stan] [R] ベクトル ARIMA (VARIMA) で人口予測 (?)

統計学 R stan 時系列分析 MCMC
この記事は最終更新日から3年以上が経過しています

概要

  1. 前回 VARMA の話をしたのに関連して, 単なるテクニカルな話題から, もう少し実用性のある話にしてみた.

  2. 都道府県別の人口の時系列データを VARIMA を当てはめてみた.

  3. 今月は時間がなかったのであまり大した内容ではない. 5ページ程度. 中途半端.

VARMA を使う意味

ただの ARMA ではなく VARMA を用いる一番の理由は, 「異なる時系列どうしの相互作用をみる」ことだと思っている. 例えば代表例としてマクロ経済モデルや株式市場の価格変動などで VARMA (VAR) がよく使われる. これは モデルの簡潔さだけでなく, Granger の因果性を見ることができるというのも大きい. 株価なら, ある産業 A 大手の株が下がれば, 産業A の 2番手の企業の株価が反対に上昇するかもしれない*1. マクロ経済なら金利に対応して設備投資がどうこう, それに応じて翌年の生産高が増減し……, のように, ベクトル化した時系列モデルは時系列どうしで互いに影響し合うような現象を表現することに長けている. ここでは詳しく書かないが*2, ここで推定した相互作用の大きさをもとしたインパルス-応答分析にも派生することでシミュレーションのような分析につなげることも大きい.

VARIMA で人口予測

マクロ経済モデルや株式市場の予測などではありきたりなので, 前回
ill-identified.hatenablog.com
で作成した MCMC を使って VARMA モデルを推定する stan プログラムをもとに, 都道府県別人口予測をできないかやってみた.

都道府県別の人口は, 仮に全国合計では増減がなくても, 転入出者がいるために増減が発生するので, このような人口の行き来を説明するのに VARMA が使えそうだ*3.

都道府県別の人口は総務省統計局の 統計局ホームページ/日本の長期統計系列/第2章 人口・世帯 から, 2-5表の男女合計を1950年から2009年まで利用した*4.

以下は xls ファイルを読み込んで実行するまでのプログラム. xls ファイルの読み込みには gdata パッケージを使った. また, 一部欠損値があるため, zoo パッケージの補間を行う関数を使った. stan コードは前回のものと基本的に同じだが, 対数尤度も出力するようにしたのでモデル評価のために各種の情報量規準を計算できるようになった. これにともない generated quantities ブロックのみコードを追加した。


gist326d31a40dadc1a9d87ff6eb86e0d78d


この stan コードを今回も rstan を使って R で実行する.


gist93ba87d1ede8ff49fdfbde17ce9867d6


和分過程については見た目や保守性は悪くなりそうだが, 階差を取る操作は R の diff() 関数の方が圧倒的に簡単なので, 時系列データの階差を diff() で取ってから stan に投げるという形になっている*5.

また, 次数選択のために情報量基準を使うのだが, WAICを計算させてみた：Taglibro de H：SSブログ で紹介されていた WAIC の計算が簡単だったので, ここで取り上げられている waic() を使うことにした. なお, Vehtari and Gelman (2014) の waic() 関数は Vehtari, Gelman, and Gabry (2015) によると loo パッケージに含まれているので, そちらを使う.

で, VARMA (1,0,1) として実行した結果...

1 chains, each with iter=2000; warmup=1000; thin=1; 
post-warmup draws per chain=1000, total post-warmup draws=1000.

              mean se_mean sd  2.5%   25%   50%   75% 97.5% n_eff Rhat
Psi[1,1,1]    0.92       0  0  0.92  0.92  0.92  0.92  0.92     1    1
Psi[1,1,2]   -1.66       0  0 -1.66 -1.66 -1.66 -1.66 -1.66     1    1
Psi[1,1,3]   -0.31       0  0 -0.31 -0.31 -0.31 -0.31 -0.31     1    1
Psi[1,1,4]    0.97       0  0  0.97  0.97  0.97  0.97  0.97     1    1
Psi[1,1,5]   -0.30       0  0 -0.30 -0.30 -0.30 -0.30 -0.30     1    1
Psi[1,1,6]    1.98       0  0  1.98  1.98  1.98  1.98  1.98     1  NaN
Psi[1,1,7]    0.62       0  0  0.62  0.62  0.62  0.62  0.62     1    1
Psi[1,1,8]    1.49       0  0  1.49  1.49  1.49  1.49  1.49     1    1
Psi[1,1,9]    1.65       0  0  1.65  1.65  1.65  1.65  1.65     1    1
Psi[1,1,10]   1.55       0  0  1.55  1.55  1.55  1.55  1.55     1    1
Psi[1,1,11]   0.86       0  0  0.86  0.86  0.86  0.86  0.86     1    1
Psi[1,1,12]   0.80       0  0  0.80  0.80  0.80  0.80  0.80     1    1
Psi[1,1,13]   1.81       0  0  1.81  1.81  1.81  1.81  1.81     1    1
Psi[1,1,14]  -1.72       0  0 -1.72 -1.72 -1.72 -1.72 -1.72     1    1
Psi[1,1,15]  -0.08       0  0 -0.08 -0.08 -0.08 -0.08 -0.08     1    1
Psi[1,1,16]   0.99       0  0  0.99  0.99  0.99  0.99  0.99     1    1

なんだか係数が胡散臭い値になっている……?

グラフにしてみる. 47系列あるので, ここでは北海道, 東京, 大阪だけを出力した.

f:id:ill-identified:20160402222933p:plain

ということで, 明らかに発散してしまっている. そもそも原系列をプロットしてみても,

f:id:ill-identified:20160402223213p:plain

こんな感じである. 人口が一定水準まわりで変動し続けるというのも直感的でないので, 定常ではなくトレンド定常を疑ったほうが良いだろう. また, 都道府県も関東のみにした.

適切な次数を探索する方法もいくつか存在するが, 今回は時間がなかったので, p, q の次数選択を, 0 から 2 の範囲で WAIC で選ぶようにした. d は手動で調整した*6.

結果, VARIMA(1,1,0) が選ばれ, その予測区間が以下のグラフである (2010年以降の実線が期待値, 破線が中央値, 青色が90%, 灰色が95%区間. ).


f:id:ill-identified:20160402225613p:plain

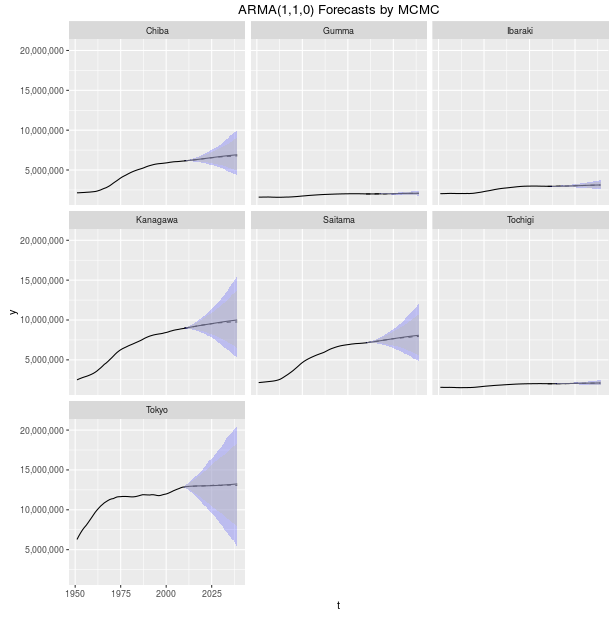
それっぽくなったが, よく政府の人口推計で指摘されているような人口減少の感じはしない. 理由は2つ考えられ, 1つは年齢別人口ではないことを挙げる. 実際には少子高齢化は年齢分布が歪になって起こるが, このデータではその情報は得られない*7. もう1つは, パラメータ自体も変化しているということが考えられる. 毎年の出生率は変化しているが, ARIMA は固定されたラグ説明変数の係数と線形トレンドで表現されるので, この事情は反映されない. 後者については, 可変パラメータモデルを利用すれば変わるかもしれない? また, 人口を扱うことから, ポアソン分布を使うという方法もあるが, めんどくさかった*8ので今回はやらなかった. もう少し込み入ったモデリングの話と実践はまた今度.

参考文献


Vehtari, Aki, and Andrew Gelman (2014) “WAIC and Cross-Validation in Stan,” May: 1–15. http://www.stat.columbia.edu/~gelman/research/unpublished/waic_stan.pdf.

Vehtari, Aki, Andrew Gelman, and Jonah Gabry (2015) “Practical Bayesian Model Evaluation Using Leave-One-Out Cross-Validation and WAIC,” no. July (July). http://arxiv.org/abs/1507.04544.

沖本 (2010) 経済・ファイナンスデータの計量時系列分析. 朝倉書店.

経済・ファイナンスデータの計量時系列分析 (統計ライブラリー)

経済・ファイナンスデータの計量時系列分析 (統計ライブラリー)

  • 作者:沖本 竜義
  • 出版社/メーカー: 朝倉書店
  • 発売日: 2010/02/01
  • メディア: 単行本

*1:この辺は詳しくないので適当.

*2:沖本 (2010) などを参照

*3:ちょっと調べたらわかるが, 人口予測にはいろいろな方法があり, VARMA は必ずしも最適な方法ではないが, 他に適当な多変量の時系列データを思いつかなかったのでこうなった.

*4:国勢調査は5年ごとで, それ以外の年は実測値ではなく補間になるのだが, 今回は厳密さはあまり重視しないのでそのまま使った.

*5:ただし, トレンドの処理で, グラフを描く関数は1次の和分過程までにしか対応していない.

*6:なお, d=0 よりも d=1 で明らかに WAIC が改善されていた.

*7:統計局では年齢別人口も公開されているが, 今回はあくまで限定されたデータで推定できるか, という話にしている.

*8:stan で整数を扱うのは少し難しい

ill-identified 読者になる

広告を非表示にする
コメントを書く