概要
bsts とは, Bayesian Structural Time Series, つまりベイズ (ベイジアン) 構造時系列モデルの略称である. 某有名IT企業の某有名データサイエンティストの方が bsts パッケージの入門記事
tjo.hatenablog.com
を書いていたが, より詳細で広範な説明がほしいところであった. 奇しくも bsts の開発者もこの方と同じ企業に所属しているので, 何か特別な思い入れがあるのかとも思ったが, 本人はなかなかより詳細な記事を書く気配がないため, しびれを切らして自分が書くことにした (あてつけではない).
この記事の残りの構成は次の通り. まず, 第2セクションではベイズ構造時系列モデルとは何か, 理論的な解説をする. 実際にはこのセクションはほぼ S. Scott & Varian (2013, Bayesian Variable Selection for Nowcasting Economic Time Series), S. L. Scott & Varian (2014, Predicting the present with Bayesian structural time series) の要約である. 第3セクションでは, 実際に bsts パッケージを操作できるように構文を解説する. 第4セクションでは, 具体例に基づいて実演する.
bsts の基本理論
bsts 開発のモチベーションは, 時系列予測の中でも, 随時, 短期間の将来の状態を予測する “nowcasting” (ナウキャスティング) の実現にある. 従来的な時系列予測と異なるのは, 時系列の多さと, それとは相対的にデータの期間が短い*1ことである. 膨大なデータから予測モデル構築に有効な変数を全て人の手で取捨選択するのは困難である*2. このような状況で, 予測モデルを構築するにあたって重要な機能は
時系列モデル特有の要素 (定常トレンドや周期トレンドの要素)
変数選択 (スパース推定)
モデル平均化法 (model averaging)
の3つである. つまり, これまでの時系列予測モデルが比較的長期の予測を可能とするモデルや, 時系列モデルの構造の同定も含めて興味の対象となってきたのとは対照的に, ベイズ構造時系列モデルは近視眼的な当てはまりだけを重視する機械学習的なアプローチをしている.
時系列モデル特有の要素
(1) は, 状態空間モデルをカルマンフィルタで計算すれば, 容易である. 状態空間モデルを用いれば, ローカルレベルトレンドや季節性トレンドと回帰モデル(係数が変動する dynamic regression を含む) をミックスしたモデルもカルマンフィルタで計算が可能になる. これは以前にいくつかの記事で言及したので, これ以上の説明は省略する.
ill-identified.hatenablog.com
ill-identified.hatenablog.com
変数選択
状態空間モデル,
の上段の式が観測方程式, 下段が遷移方程式 (状態方程式) である. 観測方程式の係数行列 は, 時間によって変化させることもできる. つまり, 毎期
ごとに値が変わってもモデルの計算は可能である. よって,
の成分に, 毎期で値の変わる説明変数を与えることで, 回帰モデルとして扱うこともできる. この場合, 対応する状態変数
の成分が回帰係数に対応する. 状態変数も値を変化させることができるが, この変数選択の場面では, 全期間を通して値が一定の場合のみを考える.
しかし, 先に書いたように, 今は説明変数の候補が非常に多い状況を考えている. 無意味な説明変数を増やすことは計算の困難さや過剰適合 (オーバーフィット) にもつながるので, 必要最小限の変数だけを選択しなければならない. 回帰モデルの変数選択といえば, Lasso (L1 正則化) やリッジ回帰 (L2正則化) のようなスパース推定, あるいは主成分回帰 (PCR) など, 様々な方法があるが, bsts は George & Mcculloch (1997, Approaches for Bayesian Variable Selection) によって提案された spike-and-slab 事前分布を使うというベイズ的な方法を採用している. スパース推定と事前分布の関連がよくわからないという人は, 以下などを参考にしてほしい.
説明変数の係数 について,
という指示変数を用意する.
は係数
がゼロでないなら1, ゼロならゼロとなる.
がゼロでない説明変数だけが, 実際に使われることになるから, まずは
の事前分布を考える.
となる確率を
とおくと,
の事前分布は
と設定する. ただし,
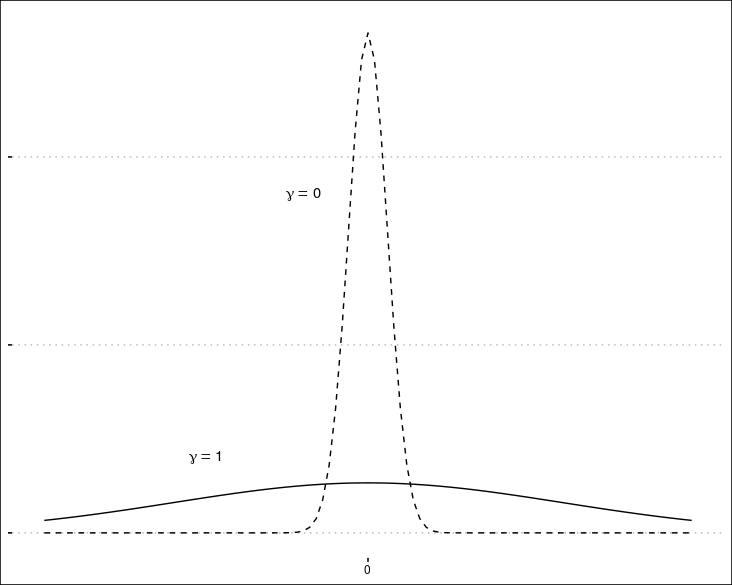
(2018/8/9: spike-slab 事前分布の意義についてよくわからない説明していたので修正)
ではなぜ, よく用いられる L1, L2 正則化を使わず, この事前分布を採用したかだ. 機械学習の L1, L2 正則化は, それぞれベイズ統計ではラプラス分布と正規分布を事前分布に設定するのと同じで, 特に L1 正則化 (=Lasso) は変数選択についてよく似た性質を持つし, 計算ももっと簡単なはずだ. なぜこのような複雑な事前分布を考えたのか. 本文では L1 正則化に比べてどこが優れているかを明示していない*3ので, 私なりの考えを述べる. まず1つは, 既に書いたようにハイパーパラメータ の調整でどの程度の変数が排除されるのか直感的にわかりやすいという点があるだろう. ここでは変数が観測数よりも多いような状況も想定しているので, スケールパラメータをどの程度増減させれば変数がどれだけ排除されるかすぐにわからない L1 正則化よりも使い勝手がよい, ということなのだと思う. 一方で, 一旦採用されてしまえば, L2 正則化と同様に,「緩やかな」縮小推定がなされ, 過剰に係数の大きさが抑制されることがなくなる. しかし, このような事前分布では, どの変数が選ばれるかがかなり偶然に左右されるため, 重要な変数を落とす可能性が増えてモデルの予測値にも大きなばらつきが出ると思われる. その点については, 次に紹介するモデル平均化法で対処しているのだと思われる.
モデル平均化法
(2018/8/10: モデル平均化の意味を最近まで分かっていなかったことを告白しつつ, 説明を刷新)
bsts ではベイジアンモデル平均化 (BMA) というテクニックが使われている. これについて本文で参照されているページは現在は存在しなかったので, 関連が深いと思われる Hoteling et al. (1999, Bayesian Model Averaging: A Tutorial) を参考にする*4. BMA は, 要するに機械学習でいうアンサンブル学習と同じアイディアである. バイアスは小さいがバリアンスの大きい複数のモデルの予測値を平均し, バリアンスを低減することで予測精度を上げるというテクニックは, ランダムフォレストやバギング, スタッキングなどのアンサンブル学習のテクニックと同じである.
今回のモデルは予測分布をモンテカルロサンプリングで得られるので, 1つの に対して複数の予測値を与えられる. しかし BMA はそういう話ではなく, モデル自体を複数作成することを考える. ベイズモデルは, モデルの事後確率*5を定義できるため, これをウエイトにして各モデルの予測値の加重平均を取ることで, 単純平均よりも当てはまりを良くしている. これが BMA の基本アイディアである.
ただし実際には, あまりに性能の悪いモデルが含まれていると平均化は上手くいかない. 機械学習の応用でも, 複数のモデルから得られる予測値をそれぞれ単純平均, あるいは目分量で加重平均して統合しただけで精度が良くなる (経験損失が小さくなる) というケースはよく見かけるが, BMA はこれを理論的により精緻にしたものと言える. Madigan & Raftery (1994) では, 相対的に確率の低い値で, かつ一定の水準以下のモデルを排除する, 複雑度のより大きいモデルを排除する, といった情報量規準に似たルールでモデルを取捨選択することが提案されている. さらに別の方法として, メトロポリス-ヘイスティングスアルゴリズムを使ってモデルを複数サンプリングすることで, モデル平均を直接計算する MC3 アルゴリズムというものも提案されている*6.
bsts の利点
ベイズ統計モデルとして定式化すると, 事後分布が複雑であっても計算できるマルコフ連鎖モンテカルロ法 (MCMC) で対応できる. MCMC は計算が遅いと言われているが, 一部のパラメータに共軛事前分布を用いて事後分布が陽に得られるなら, ギブスサンプラーが使えるから, 計算も比較的高速になる. spike-and-slab 分布は一見複雑に見えるが, 実は一部をギブスサンプラーでサンプリングできる.
bsts の構文と使用法
状態空間モデルとして記述されたモデルを扱うため, 状態空間モデルの特徴を記録するオブジェクトが必要である. bsts では list オブジェクトが用いられ, 記述を追加するには Add で始まる各種関数を用いる. 例えば, ローカルレベルモデルならば,
ss <- AddLocalLevel(state.specification=list(), data$y)
となる. これで ss という list オブジェクトに, ローカルレベルモデルの記述がなされた. AddLocalLevel() 関数は, 第1引数に状態空間モデルを記述するオブジェクトを与えると, そのオブジェクトにローカルレベルの要素を追加したものを返すという処理をするが, ここではゼロから作るため, 空の list を与えている. 既存のリストオブジェクトにローカルレベル要素を追加したい場合は, ここに追加先のオブジェクトを指定することになる. 第2引数 data$y は観測された時系列データである. この ss に4期間周期の季節性トレンドを追加するならば,
ss <- AddLocalLevel(state.specification=list(), data$y) ss <- AddSeasonal(ss, data$y, nseasons=4)
というふうに記述する. 観測データは毎回与える必要がある. その他にも, 休日効果を追加する関数や, trigonometric trend を追加する関数もある. 変化点を与えるものは今のところないようだ.
このような構文になっているということは, 当然 magrittrのパイプでつなげることができる. ここまでの, ローカルレベル+季節項のモデルは, パイプを使って以下のようにも書ける.
require(tidyverse) list() %>% AddLocalLevel(., data$y) %>% AddSeasonal(data$y, nseasons=52)
記述が終われば, 次に予測を行う. 先に書いたように, bsts パッケージは完全にベイズ的な方法でなされるため, dlm や kfas と違いパラメータ推定と予測が bsts() という1つの関数で行われる. bsts() では, 観測方程式の分布族や MCMC の試行回数, (必要ならば) 回帰する説明変数の指定などを指定できる. なお, ここで指定した説明変数には, 自動で spike-and-slab による変数選択が適用される.
bsts() 関数の返した結果の格納された bsts オブジェクトを, plot() 関数に与えることで結果を様々なグラフで表示できる. たとえば, "coefficients" または "coef" オプションを追加した場合は, spike-and-slab によって選別された説明変数が, モデルに含まれる確率がプロットされる (棒グラフに影がついているものは係数がマイナスであることを意味する.).

さらに, "components" または "comp" ならば時系列をローカルトレンド, 季節トレンド, といった部品に分解したものがプロットされる.
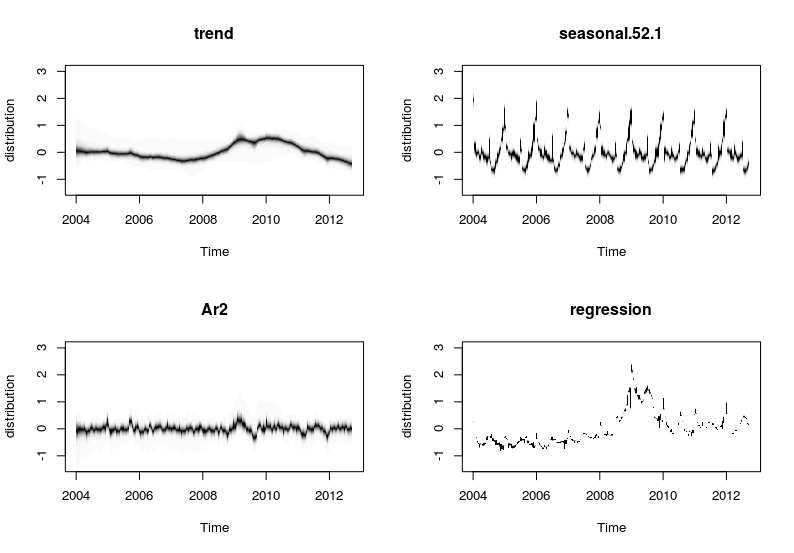
予測を求めたいなら, これもシンプルで, predict() 関数と plot() 関数を使うだけである*7.
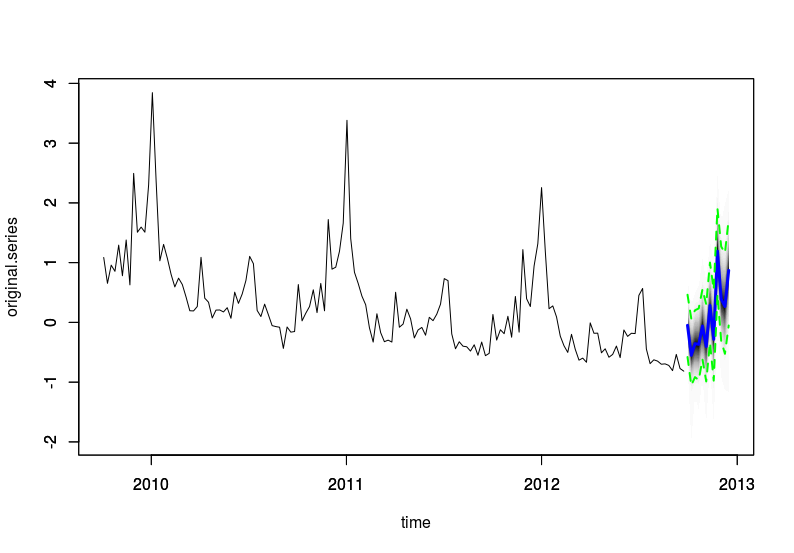
さらに, 複数のモデルを用意した場合, CompareBstsModels() 関数で複数のモデルの誤差を比較できる.
実験
現行バージョンでは, 周期トレンドはカレンダー効果と固定周期のトレンドしか指定できないため, 日次単位のデータや四半期単位のデータは有効だが, 時間単位でありながら数カ月あるような長期データなどを扱うのは難しい. また, 前回の動的市場反応モデル も, どの変数を使うべきかが理論モデルからある程度決まっているので, bsts の用途と合致しない. この要件をみたす実験用データを探すのは面倒なので, 結局, 公式の解説で使われているのと同じデータを用いることにした. このデータには米国の毎週の失業者数*8が記録されている. 失業者数のような政府統計はふつう, まず不正確な速報が発表されてから, しばらくして確報が発表される. そこで, より早く最新の失業者数を知るために, 失業者数の予測モデルを作るモチベーションが発生する. 失業者数の発表は木曜日で, グーグルのログは最新でも2日前のものしか利用できない.
公式では, 3種類のモデルを設定し比較しているが, 元記事そのまんまでは面白くないので, 適当に2つほどモデル候補を追加してみる.
ローカルレベル + 季節トレンド(52週間(=1年)で1周期のトレンド)
モデル (1) + 説明変数
モデル (2) の係数の事前分布を緩和 (係数がゼロになりにくい)
(2) に2階の自己回帰項 AR(2) を追加する (係数には spike-and-slab が適用される).
(4) の回帰を dynamic regression にする (spike-and-slab は適用できない).
プログラムは以下のとおりである.
gist4bb6fdc0714122bec7b12d2f1422e7c8
モデル (5) は, 係数が時変パラメータであるため, "coef" が使えない. かわりに "dynamic" ("dyn") オプションをつけて平滑化推定量をプロットする.

CompareBstsModels() を使った各モデルの比較結果は以下のようになる. 2つの時系列グラフが出力され, そのうち, 上段は各モデルの1期先予測値の誤差の絶対値の累積値で, 下段は観測値のスケールを調整した時系列である. このグラフにより, 時系列のどのあたりで予測精度が悪くなっているか, その原因は原系列の構造変化ではないか, といったことを端的に知ることができる.

モデル (4) は元記事で提案された (2), (3) の精度に近いが, モデル (5) は, 最初は誤差が小さいものの, 2009年 (おそらくリーマン・ショック) を境に誤差が積み重なっている. おそらく過剰適合しているのだろう.
蛇足: 状態空間モデルつながりで, KFAS についてもそのうち解説記事を書こうかと思う. 同じく状態空間モデルで有名な dlm は既に のように充実した解説が存在する.
追記: KFASパッケージの解説を書いた.
ill-identified.hatenablog.com
参考文献
- George, E. I., & Mcculloch, R. E. (1997). Approaches for Bayesian Variable Selection. Statistica Sinica, 7, 339–373. Retrieved from here
- Hoteling, J. A., Madigan, D., Raftery, A. E., & Volinsky, C. T. (1999). Bayesian Model Averaging: A Tutotial. Statistical Science, 14(4), 382–401. doi:10.1214/ss/1009212519
- Madigan, D., & Raftery, A. E. (1994). Model Selection and Accounting for Model Uncertainty in Graphical Models Using Occam’s Window. Journal of the American Statistical Association, 89(428), 1535. doi:10.2307/2291017
- Scott, S. L., & Varian, H. R. (2014). Predicting the present with Bayesian structural time series. International Journal of Mathematical Modelling and Numerical Optimisation, 5(1/2), 4. doi:10.1504/IJMMNO.2014.059942
- Scott, S., & Varian, H. (2013). Bayesian Variable Selection for Nowcasting Economic Time Series. NBER Working Paper Series, 1–22. Retrieved from here
*1:Google の検索ログは膨大だが, 2004年からしかない.
*2:これを著者らは 'fat regression' と呼んでいる.
*3:George & Mcculloch (1997) でも言及されていない
*4:なお, ぐぐると『パターン認識と機械学習』の勉強会スライドがいくつもヒットするので, こちらでもBMAが解説されているようだ.
*5:ベイジアン情報量規準 (BIC) はこの確率の対数を近似している
*6:アイディアが直球すぎて笑ってしまった.
*7:ただし, 回帰モデルを含む場合は, 予測のために将来の説明変数データも必要になる
*8:正確には initial claims number; 失業者による初回の失業給付申請件数. また, データセットに収録されている数値は未加工のカウントデータではなく標準化したものである