
- イントロダクション
- モンテカルロ法とは
- どこを見て収束を確認するか
- トレースプロット
- GR統計量 を確認する.
- 自己相関関数 (ACF, コレログラム)
- 有効サンプルサイズ
- 事後診断ツール bayesplot
- こういう時どうすればいい?
- まとめ
- 参考文献
イントロダクション
この投稿は, 第78回R勉強会@東京(#TokyoR) - connpass での LT の内容を加筆修正したものである. 以下は当時のスライドである.
以前, Tokyo.R かどこかの懇親会で, マルコフ連鎖モンテカルロ法 (MCMC) について「便利だというが正しい使い方がよくわからない. 特に収束しない場合はどうすればいいのかわからない.」という話を聞いた. 自分でも調べてみたところ, 確かにこの辺の話題があまりない. ネット上のブログ等では, MCMC のライブラリを使ってみたとか, 特定のモデルについて計算してみたとかそういう記事はたくさんあるのだが, 収束の判定をどうやってるのかということに詳しく言及しているものはほとんどない. これは英語圏でも同様で, 日本語よりは情報が多いが, それでも断片的である. つまり, 実用的な情報が不足している.
というわけで, 今回は収束の手順と, うまく行かない場合にどうすればいいかというアドバイスを, R の rstan と bayesplot パッケージを使いながら紹介する. ただし, LT 用に作った資料なので, そこまで網羅的ではない. 例えば, 各分野の学術論文誌にアクセプトされるにはどういう作法で MCMC をすれば良いかというような話はできない. さらに, 今回の記事は既にどこかの教科書・論文で指摘されている内容を引用しているのがほとんどだが, これらの文献どうしでもたまに互いに矛盾する記述がある. これらは実際には致命的な誤りではないのだが, 説明が不明瞭と感じる箇所が多い. これらを整理するのが今回の記事の重要な部分だと考える.
20205/21 追記: 最新の話題についても言及した. もしかしたらその内1つの記事にまとめるかもしれない
ill-identified.hatenablog.com
モンテカルロ法とは
マルコフ連鎖モンテカルロ法 (以下, 単にモンテカルロ Monte-Carlo 法) は一般には乱択アルゴリズムの一種だが, ここではベイズ統計モデルのパラメータの事後分布を効率よくサンプリングするテクニックとしての側面から説明する. パラメータが多く, 事後分布を陽表的に得られないモデルは, 従来の最適化アルゴリズムで解を計算するのが難しい. 最も単純なモンテカルロ法は, パラメータの候補として乱数を生成し, その乱数に対応する確率を計算することである. しかし, このような総当り的な方法は全く効率的でなく, パラメータの数が増えると飛躍的に時間がかかるようになる.
そこで, 完全にランダムではなく, 1つ前の乱数をもとに少しづつ確率の大きな値を探索しつつ次の乱数を生成していくアルゴリズムが考えられた. これがマルコフ連鎖モンテカルロ法である. この方法であれば, 十分な回数だけ乱数を生成すれば, 乱数列は事後分布から生成したものと同等になる. 分布の収束先を定常分布 (stationary distribution) という. 適切な定常分布に収束しているならば, この行程で得られた乱数列 (これをモンテカルロ・サンプル, 以下, 単にサンプルという) は, 互いに独立な事後分布のサンプルと見做すことができるので, 事後分布の形状やパラメータを推定することができる*1. 正規分布なら平均値と中央値と最瀕値がすべて等しいので何もしなくてもほぼうまく行くが, しかし, そんな簡単な問題にわざわざ MC 法を使う必要はない. そこで, 複雑なモデルにモンテカルロ法を適用した場合, 定常分布に収束できているのかを生成されたサンプルから確認する必要がある.
どこを見て収束を確認するか
今回は主に Gelman, A. et al. (2013, Bayesian Data Analysis) の Ch. 11 で紹介されている方法を参考にするが, このテキストは理論の説明がメインであり, 実用上の注意点がやや乏しい. しかし, これ以外の文献もまた, 説明が充実しているとは言い難い. 他の比較的まとまった記述として, 松浦 (2016, Stan と R でベイズ統計モデリング) (アヒル本) 2章4., 4章 4.7-4.9 や, 古澄 (2015) の 3.4 節, そして以下のサイトが参考になる.
また, stan のマニュアルにも, 断片的だが特定のケースでの収束を解決する方法の記述がある.
トレースプロット
サンプルを時系列プロットしたものをトレースプロット (traceplot) と呼ぶ. 適切なモンテカルロ法で得たサンプルは, 互いに独立であるはずなので, ランダムウォークのようにはならないはずである. そのため, 「毛虫のような」トレースプロットが望ましいとされる (図 2). しかし, トレースプロットが「毛虫っぽい」かどうかはかなり主観的な判断になってしまう. トレースプロットからはいろいろな情報を読み取れるので利用価値はあるが, 先に, 収束しているかを確認するためのもっと厳密に定義されたルールを紹介する.

GR統計量 を確認する.
を確認する.
サンプルが定常分布に収束しているかを確認する指標として がある.
と呼ばれる統計量は複数あるが, 今回は Gelman & Rubin (1992) で提案された potential scale reduction factor (PSRF, 提案者の名前から, Gelman-Rubin 統計量とも呼ばれる) を使う.
が系列
*2 の
番目のサンプルで, 事後分布が正規分布であるとすると, 系列間分散 (between-chain variance)
と系列内分散 (within-chain variance)
で, 以下のように表される.
サンプルが適切な事後分布から生成され, かつサンプルサイズが十分大きければ,
”If is not near 1 for all of them, continue the simulation runs. The condition of
being ’near’ 1 depends on the problem at hand, but we generally have been satisfied with setting 1.1 as a threshold.“
とあるので, すべてのパラメータに対して となれば*3「収束した」と判断する.
beyesplot では, mcmc_rhat() と, サンプル配列から を計算する
rhat() を使い, 簡単に確認することができる (図 3).
ヘルプによれば, summary(stanfit) で表示されるのも, coda::gelman.diag() で表示されるのも, PSRF である*4.
なお, 他の定義として, Brooks & Gelman (1998) で紹介されている corrected scale — (CSRF) がある. また, 全く異なるアプローチで収束をチェックする方法も提案されている (Heidelberger & Welch (1983), Raftery & Lewis (1991), Geweke (1992) など).
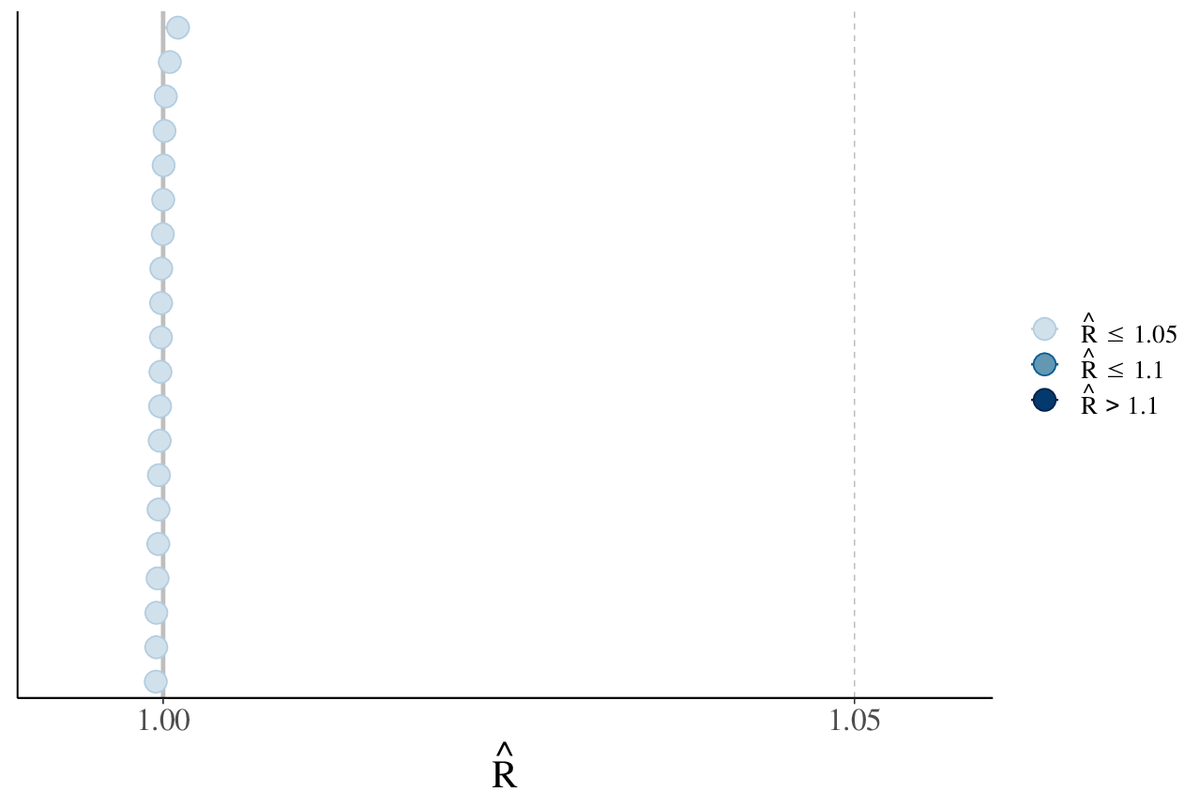
bayesplot での PSRF のプロット例
多重連鎖はいくつ必要か
多重連鎖が具体的にいくつあると良いか, という問いに対して明確な答えを見つけることはできなかった. stan ではデフォルトで4つの連鎖を生成するようになっているが, 古澄 (2015) では「現在は単一連鎖のほうが良く用いられている」とあり, 矛盾している. ただし, むしろその結論に至るまでの議論に注意すべきである. 単純に考えれば単一連鎖と多重連鎖に同じ時間を掛けた場合, 後者の1つ1つのサンプル列は短く, 分布が収束していない恐れがある. よって単一連鎖を用いよという主張は, 収束のためにサンプルサイズを十分大きく取れという意味だとわかる. しかし, 実際に計算をただ1回で成功するとは限らず, 局所解に陥ってないかを確認するためには異なる初期値で何度か計算してみる必要がある. 複数の連鎖で計算するのは, 局所解に収束しないことをチェックを兼ねており, 初期値を変えて何度も試すという数値計算の基礎に則したものである. よって, 私は次のように考える. 局所解を排除し計算の安定性を向上させるのが目的であり, 連鎖の数を金科玉条のごとく守る必要はない. 連鎖の数やそれぞれのサンプリング回数は計算資源やモデルの巨大さと相談して決めれば良く, 固定的な決まりはない, と.
自己相関関数 (ACF, コレログラム)
サンプルが定常分布に収束しているとき, サンプル列は互いに独立になっているはずである. よって, サンプル列の自己相関係数 (autocorrelation coefficients) の列 (自己相関関数, ACF*5 という) をプロットして確認することも重要になる. 自己相関係数の詳しい話は時系列分析の教科書 (北川 (2005, 時系列解析入門), 沖本 (2010, 経済・ファイナンスデータの計量時系列分析)) などを見て欲しい. 自己相関係数が低いことが求められているため, ラグ=1 以降, ラグ次数の増加に伴って自己相関係数の絶対値 (現実的にはモンテカルロ法で自己相関係数が完全にゼロになることは少ない) が急速に減少し, ゼロに近い値になるようなサンプルが好ましい (図 4).

bayesplot での自己相関係数プロット
有効サンプルサイズ
そもそも自己相関係数が大きいと, 統計推論での基本である中心極限定理が意味をなさなくなり, 分散を正しく推定できなくなる. すると, 事後分布の平均値がどの程度の誤差を持つかについても, 正しく推定できなくなる. よって, サンプルの収束確認には平均の収束を表す だけでなく, 分散の観点から別のチェック項目が必要になる. Gelman, A. et al. (2013) や 古澄 (2015) によると, 漸近分散の公式を変形して導出した, 有効サンプルサイズ (effective sample size; ESS) というものがある. 簡単に, 1系列しかない場合についてパラメータの自己相関係数を
とすると, 有効サンプルサイズ
は
と定義される. よって, 自己相関が小さいほど は大きくなり
に近づき, 逆に自己相関が大きければ
は小さくなるはずである. 有効サンプルサイズの概念を別の視点から説明し直すと, こうなる. 仮にサンプルが適切に生成されているのなら, 各サンプルは互いに独立で, 中心極限定理が適用できるはずである. そのため, 中心極限定理の漸近分散から逆算して, サンプルサイズも計算できる. よって, 逆算したサンプルサイズと実際のサンプルサイズとを比較することで, 独立なサンプルからどれくらい離れているかを見ることができる, ということである.
stan のデフォルトアルゴリズムである NUTS では, 事後分布が正規分布に近く, パラメータ間の相関がない場合は となるはずである.
実際には は求められないので, stan では標本自己相関係数を使って
の推定値
を求める.
のときと同様に
個の系列があるとして, サンプル列
のあるパラメータの標本自己相関係数を
とすると,
は以下のように定義される.
ここでは, が
に近いことが望ましい. これを
と同様に, すべてのパラメータに対して計算する (図 5). Gelman, A. et al. (2013) では, 少なくとも
を満たせば十分に自己相関が消滅しているとみなす, というルールを提案している*6. 有効サンプルサイズは実質的なサンプルサイズと見なすことができ, パラメータの標準誤差は
のオーダーで減少していく. 要求される精度に応じて, 有効サンプルサイズの目標も調整すればよいだろう.

bayesplot での有効サンプルサイズのプロット例
なお, その他にも, 自己相関の大きさを1つの量で表現する方法として, 効率性因子 (efficient factor) というものも存在する.
事後診断ツール bayesplot
以上で述べた項目を確認するツールとして, 松浦 (2016) やほぼ同時期に投稿した私のブログでは ggmcmc パッケージを紹介していた.
しかし現在は bayesplot というのがより便利である. ちなみに先行する日本語の紹介記事には以下のようなものがある.
Bayesplotパッケージはいいよ – Kosugitti's BLOG
が, 非常にシンプルな構文なのであまり覚えるべきことはない. 以下の 3原則だけを覚えれば良いだろう.
mcmc_*で始まる一連の関数でサンプルの診断結果をプロットするggplotオブジェクトと同じように扱えるサンプルを3次元配列で入力する
グラフを描画するのは主に, mcmc_*() の関数群である. 例えばトレースプロットなら mcmc_trace(), 自己相関係数なら mcmc_acf_bar() である. rstan の最近のバージョンでも, このようなグラフをサポートするようになってきており, 機能面ではさほど大きな差はない. しかし, パラメータが非常に多い場合に や
の値がどれくらい基準に届かないかを一望できるグラフを描くなど, 特殊な場合で役に立つ関数も充実している.
2つ目の利点として, bayesplot の出力するグラフは ggplot オブジェクトである, という点がある. これは ggplot2 のグラフと同じように扱えることを意味し, scale_*() 関数や theme() 関数などでデザインを手軽に変更できることを意味する. もちろん, ggthemes のプリセットテーマを与えることもできる.
最後に, bayesplot の 入力は stanfit ではなく, ggmcmc と同様に3次元配列オブジェクトである. Stan の開発チームが bayesplot を開発しているにもかかわらず, だ. しかし逆に, この仕様のため bugs や rjags のような他のライブラリで計算した MC サンプルを入力するのも容易になっている. stanfit は as.array() を使うだけで3次元配列に変換できるので, この仕様で作業が特別に面倒になることはないだろう. ただし, を表示する
mcmc_rhat() など一部の関数は, ベクターを引数にとる. そういう場合も, 3次元配列からベクターに変換する関数も用意されている. の場合は,
rhat() 関数を間に挟めば良い.
こういう時どうすればいい?
以上から, 見るべきは各パラメータの と
である. しかし, いざやってみてうまくいかなかった場合は, 単純化した指標だけを見るのではなく, トレースプロットや自己相関係数プロットも確認することで, どう改善すべきかのヒントが得られる.
GR統計量 の値が大きい
の値が大きい
最も単純な対処法は, 試行回数を増やしてサンプルサイズを大きくすることである. また, 開始直後のサンプルは初期値から定常分布への過渡期にある (burn-in) ため, この部分をサンプルから除外してもよい stan で採用されている NUTS (Hoffman & Gelman, 2014, The No-U-Turn Sampler: Adaptively Setting Path Lengths in Hamiltonian Monte Carlo) では, 体感だが bur-in の問題はあまり発生しないことが多い. 基本的な MCMC アルゴリズムの1つであるメトロポリス・ヘイスティングス (Metropolis Hastings; MH) 法は, burn-in の期間を手動で調整したり, 提案分布のパラメータ次第ではサンプル列がなかなか収束しない低速混合の状態に陥ったりする場合もあるが, この点 NUTS はある程度自動調整してくれるため, あまり気にしなくても良いという利点がある. アルゴリズムに由来するサンプリングの非効率さについては後でまとめて説明する.
具体例を紹介してみる. トレースプロットを見ると, サンプル系列がゆるやかに遷移するだけでいつまで経っても特定の値に収束せず, それぞれの系列が全く違う値になっている, ということがある(図6). または, ある値に収束したと思ったら, 今度は違う値にジャンプしてしばらく収束し, またジャンプする, といったことがある. この場合も試行回数を増やしても収束しないことが多い. このような場合は, 収束が遅いのではなく, そもそもモデルが収束しないような設定になっている場合がある.
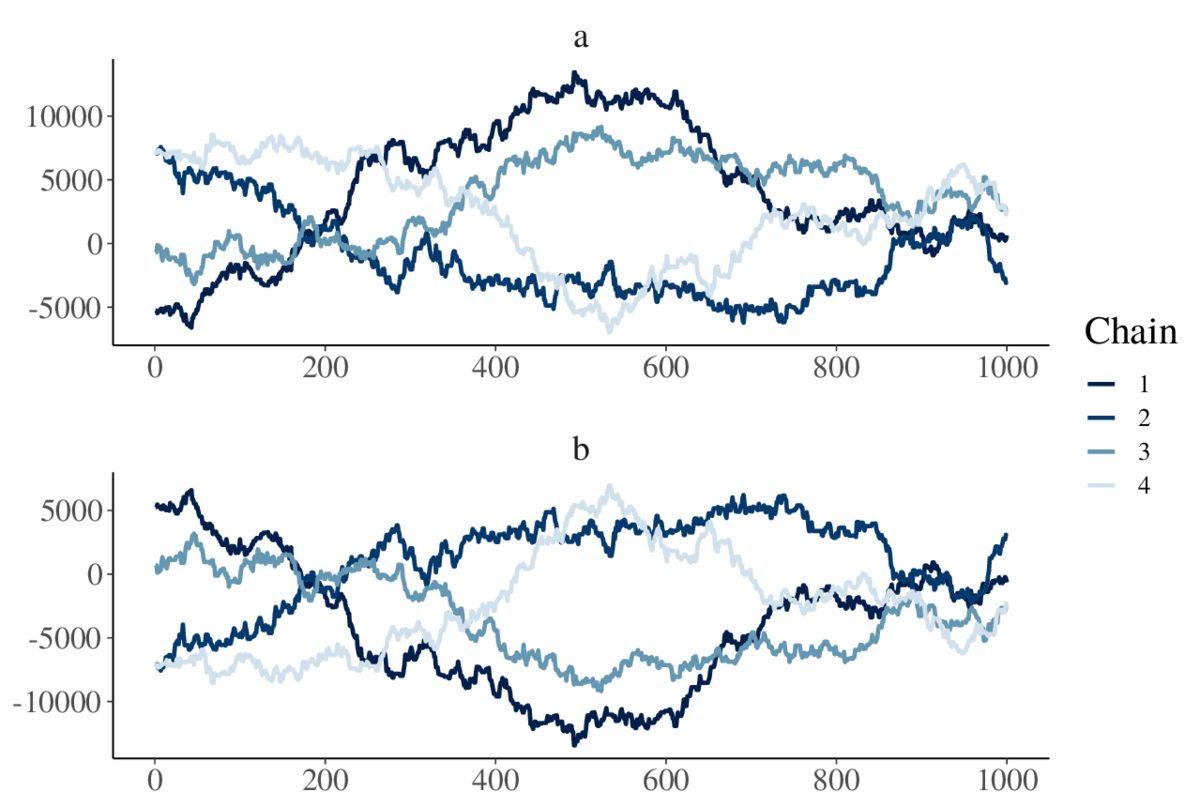
複数のトレースプロットを同時に見て, あるパラメータが下に推移するのと同時に, 別のパラメータが上に推移していた場合はパラメータが一意に定まらないモデルである可能性濃厚である. あるいは, ペアプロットでパラメータどうしの散布図を作成するのも良いかも知れない. この図では, 例えば chain 1 を見ると, 500回目くらいで a の値が大きくなり, 同時に b の値がマイナスになっており, そして両端では大小関係が逆転している. これは, RPubs - 世界一簡単な収束しないStanコード を参考にしたもので,
というモデルからのサンプルである. 事前分布の分散が大きく, また2つのパラメータ がどんな値をとってもモデルの尤度が変わらないため, いつまで経っても収束しない. 実際にこんな妙なモデルが必要になることはないが, どうしてもパラメータどうしの相関が発生するようなモデルが必要になる場合は確かにある. このような場合は, 一意に収束しやすいように事前分布で制約したり, モデルを変換 (reparametarization) したりすべきである. 類似の問題として, 松浦 (2016) の10章でラベル・スイッチング (label switching) と呼ばれる問題が紹介されている (図 7).

ラベル・スイッチングは, パラメータの収束しうる候補が複数あるため, それぞれの系列が異なる値に収束したり, 試行の途中で収束先が別の候補にスイッチしたりする, という現象である. このような場合は, 松浦 (2016) でも指摘されているように, パラメータに制約を課すなどの方法がある. 事前分布や提案分布のパラメータ調整が必要な場合もあるが, 前者は他の文献 (例えば(松浦, 2016), (奥村, 瓜生, & 牧山, 2018, Rで楽しむベイズ統計入門)) での解説が充実しており, 後者は stan ではあまりやることがないので省略する. そもそも stan は, より効率的なサンプリングを目指して考案されたアルゴリズムであり, 最も基本的な MCMC アルゴリズムである MH 法よりもうまくいくことが多い.
このように, の数値だけを見ていても
の大きい原因は特定できない. よって, どういう場合でもトレースプロットは一応確認しておいたほうが良いだろう.
アルゴリズムを変える
ここまでで上げたケースに対しては, どれもモデルを修正するという解決策を提案している. それ以外の方法として, MCMC アルゴリズムを変えるという方法もある. ただし, ここで挙げるアルゴリズムは, stan のようにオプションやドキュメントの充実した実装プログラムは存在しないため, 基本的に自分で実装する必要がある. アルゴリズムをよく理解してなければ不可能な方法である.
ピークが複数あるような多峰 (multi modal) 分布となる事後分布に対しては, MH 法でも NUTS であっても局所解に陥る可能性がある. ラベル・スイッチング問題が起こる原因の1つは多峰分布でもある. これを解決する別の方法として, Liu, Liang, & Wong (2000) の多重試行メトロポリス (multiple-try Metropolis; MTM) 法や Hukushima & Nemoto (1996) によるレプリカ交換モンテカルロ (単にレプリカ交換 replica exchange とも. 平行テンパリング parallel tempering と呼ばれることもある) 法が存在する. 名前から想像できるように, 前者は同時に複数の乱数を生成し, ランダムでいずれかを選ぶ MH 法の亜種で, 後者は同時に複数の MH 法を処理し, ある確率で別の系列の MH 法のサンプルへと推移するというものである. このようなアルゴリズムにすることで, 局所解から脱出しやすくなっている. 詳しくは原論文や 古澄 (2015) による解説などを参考にしてほしい.
または, レプリカ交換法については実装例が以下で紹介されているが, R ネイティブのコードで書かれているため, そのまま使うのは実用的ではないだろう.
有効サンプルサイズ の値が小さい
の値が小さい
すでに書いた式からわかるように, が1に近ければ有効サンプルサイズも大きいはずなので, まず
が十分小さくなったことを確認してから
を確認すると良いだろう.
が大きく, 収束していないと考えられるサンプルは, 自己相関も大きい. 図 8 は, 図7のラベルスイッチング問題のサンプルに対応する ACF である.
mu[2] の chain 1 は一応収束しているため自己相関は小さいが, それ以外の系列は自己相関が残存している. よって, の値が不適切でも自己相関が一見すると良い, ということもありうるため, 自己相関に気をつけるのは
の収束を確認してからでよいだろう.

の値が良好ならば定常分布に十分に収束している可能性が高いので, 試行回数を増やせば
も増加すると考えられる.
低速混合
もしモデルが適切に設定されているのに自己相関が残ったままであるなら, 乱数の混合 (mixing) がうまくいっておらず, 乱数の推移のばらつきの小さい低速混合の状態にあるといえる. 古澄 (2015) では, 低速混合を改善するための方法として, 相関の高い変数どうしのブロック化を紹介している.
さらに, メトロポリス・ヘイスティングス (MH) アルゴリズムでは, 低速混合とは別に, 受容確率が小さすぎる (=頻繁に同じ値が連続する) サンプルは自己相関が大きくなる. ハミルトニアン・モンテカルロ (HMC) 法の実装である stan は手動で調整をせずとも高い受容確率で推移できるので, この問題を気にする必要はほとんどない. もし, は収束したのに自己相関はどうしても改善しないという場合は……教えてください.
間引き
なお, 自己相関の大きい場合は, サンプルを 個おきに取り出して残りを捨てる, 間引き (シンニング, thinning) をすると良い, という記述を見かける. しかし, 同時に, これは生成したサンプルの一部を捨てることになる. 古澄 (2015) は間引きの効果と計算時間を天秤にかけるようにと書いているが, Gelman, A. et al. (2013) では,
を改善すると言うよりメモリを節約するのが目的の処理であるとしている. 私の考えとしては, 間引きがどの程度効果があるかは計算前にはわからない (計算後にシンニングを判断するのならば全部のサンプルを保存する必要があるため, シンニングの意味がない) ため, あまり有効なテクニックでないように思える*7.
そもそもプログラムが間違っている場合
stan や BUGS など, MCMC 用のライブラリを使わず自分でプログラムを書く必要がある場合もときにはある. この場合はモデルを間違えているだけではなく, MCMC のアルゴリズムに即したプログラムになっていない (つまりバグ) の可能性も大きくなる. この問題に対して, 古澄 (2015) は, Geweke (2004) の提案するテスト方法を紹介している. それは,
事前分布
と, 尤度
から同時にサンプル
を生成する.
から
を生成し, さらに (MCMC で求めた) 事後分布
から
を生成し,
を得る. ただし,
は
から生成する.
サンプル
と
の分布を比較する. 例えば平均値や分散値などに大きな違いがないか比較する. モンテカルロサンプルの性質から, 2群の平均値の差の検定をすることもできる.
というものである. これは, 生成されたサンプルが, 設定された事前分布と尤度に対応した事後分布から生成されているかをテストしている. 事後分布に従っているならば, (1), (2) のサンプルはどちらも同一の の同時分布から生成されているはずである, という前提に基づいている. ただし, この方法はモデルの誤り (例えばパラメータの書き間違え) もプログラムの間違えも見つけることができるが, 一方で誤りの箇所の特定まではできないだろう. 実際, MCMC のアルゴリズムは, コンセプトこそ単純だが, 実装に際して気をつけるべきことは多い. 特に乱数生成アルゴリズムに関するミスは発生しやすい. 乱数を利用するため, 発生条件の特定が難しいこともある. 伊庭 (2005, マルコフ連鎖モンテカルロ法の基礎) でも指摘されているように, 部分的に別の方法で検算することも必要になるだろう.
まとめ
かならず初期値の異なる複数系列で実行する (stan ならデフォルト設定).
の値を確認する.
トレースプロットの形状を確認する.
の値が1に近くとも不自然な形状なら原因を調べる.
を確認する. 値が小さければ試行回数を増やす.
今回の処理はすべて, 以下に書いた.
追記: 最近考案された収束の確認方法を紹介する記事も書いた.
参考文献
- Brooks, S. P., & Gelman, A. (1998). General methods for monitoring convergence of iterative simulations. Journal of Computational and Graphical Statistics, 7(4), 434–455. doi:10.2307/1390675
- Gelman, A., & Rubin, D. B. (1992). Inference from Iterative Simulation Using Multiple Sequences. Statistical Science, 7(4), 457–472. doi:10.1214/ss/1177011136
- Gelman, A., Carlin, J. B., Stern, H. S., Dunson, D. B., Vehtari, A., & Rubin, D. B. (2013). Bayesian Data Analysis (3rd ed.). CRC Press.
- Geweke, J. (1992). Evaluating the accuracy of sampling-based approaches to the calculation of posterior moments. In Bayesian Statistics 4 (Vol. 4, pp. 169–193). University Press.
- Geweke, J. (2004). Getting It Right: Joint Distribution Tests of Posterior Simulators. Journal of the American Statistical Association, 99(467), 799–804. doi:10.1198/016214504000001132
- Heidelberger, P., & Welch, P. D. (1983). Simulation Run Length Control in the Presence of an Initial Transient. Operations Research, 31(6), 1109–1144. doi:10.1287/opre.31.6.1109
- Hoffman, M. D., & Gelman, A. (2014). The No-U-Turn Sampler: Adaptively Setting Path Lengths in Hamiltonian Monte Carlo. Journal of Machine Learning Research, 15(1), 1593–1623. https://dl.acm.org/citation.cfm?id=2638586
- Hukushima, K., & Nemoto, K. (1996). Exchange Monte Carlo Method and Application to Spin Glass Simulations. Journal of the Physical Society of Japan, 65(6), 1604–1608. doi:10.1143/JPSJ.65.1604
- Liu, J. S., Liang, F., & Wong, W. H. (2000). The Multiple-Try Method and Local Optimization in Metropolis Sampling. Journal of the American Statistical Association, 95(449), 121. doi:10.2307/2669532
- Neugebauer, R. (2018). Mucha: An Illustrated Life. Praha: Vitalis Verlag Gmbh.

- 作者:Neugebauer, Roman
- メディア: ペーパーバック
- Raftery, A. E., & Lewis, S. (1991). How Many Iterations in the Gibbs Sampler?: Fort Belvoir, VA: Defense Technical Information Center. doi:10.21236/ADA640705
- 奥村, 晴彦., 瓜生, 真也., & 牧山, 幸史. (2018). Rで楽しむベイズ統計入門. (石田基., Ed.). 技術評論社.
- 伊庭, 幸人. (2005). マルコフ連鎖モンテカルロ法の基礎. In 統計科学のフロンティア12 計算統計II (pp. 1–106).
- 岩波データサイエンス刊行委員会 (Ed.). (2015). 岩波データサイエンス (1st ed., Vol. 1). 岩波書店.
- 北川, 源四郎. (2005). 時系列解析入門. 岩波書店.
- 古澄, 英男. (2015). ベイズ計算統計学. 朝倉書店.

- 作者:古澄 英男
- 発売日: 2015/10/25
- メディア: 単行本(ソフトカバー)
- 中川, 裕志. (2015). 機械学習. (東京大学工学教程編纂委員会, Ed.). 丸善出版.

- 作者:中川 裕志
- 発売日: 2015/11/01
- メディア: 単行本
- 松浦, 健太郎. (2016). Stan と R でベイズ統計モデリング. 共立出版.

StanとRでベイズ統計モデリング (Wonderful R)
- 作者:健太郎, 松浦
- 発売日: 2016/10/25
- メディア: 単行本
- 沖本, 竜義. (2010). 経済・ファイナンスデータの計量時系列分析. 朝倉書店.

経済・ファイナンスデータの計量時系列分析 (統計ライブラリー)
- 作者:竜義, 沖本
- 発売日: 2010/02/01
- メディア: 単行本
*1:モンテカルロ法のより詳しい解説は伊庭 (2005, マルコフ連鎖モンテカルロ法の基礎), 岩波データサイエンス刊行委員会 (2015, 岩波データサイエンス), 古澄 (2015, ベイズ計算統計学), 中川 (2015, 機械学習) などを参考に. 個人的には, 重点サンプリング法から順を追って徐々に複雑なモンテカルロ法へと説明をつなげていく中川本や古澄本が良いと思う. 一方で, 統計力学を学んでいるなら伊庭本のほうが馴染みやすいのかも知れない.
*2:系列が1つだけの場合は, 半分に分割する
*3:1.01や1.05としたほうが良いと紹介しているブログ記事なども見かけたが, 具体的な根拠は不明
*4:ただし, rstan の場合は1つの系列を半分に分割し, それぞれ別の系列とみなして計算するようだ: https://mc-stan.org/docs/2_18/reference-manual/notation-for-samples-chains-and-draws.html
*5:Tokyo.R の実況 TL を見ると, 自己相関「汎関数ではないか」という指摘があった. この用語について今まで注意を払っていなかったが, 時系列分析のほとんどの教科書を見ても関数 (function) と表記されていること, ACF は自己相関係数のラグの次数 (ここでは離散時間の時系列に限定しているが, ACF は連続時間にも拡張できる) に対する関数であると考えると, 汎関数とは呼ばないのではないか, と私は考える.
*6:stan の PSRF の計算方法に対応させて, 実質的には1系列あたりの有効サンプルサイズが10より大きいことを要件としている.
*7:MCMC の計算中に adaptive に間引きするテクニックがあれば有効かもしれないが, 主要な MCMC パッケージにはそのような機能は実装されていない.

![Rで楽しむベイズ統計入門[しくみから理解するベイズ推定の基礎] (Data Science Library) Rで楽しむベイズ統計入門[しくみから理解するベイズ推定の基礎] (Data Science Library)](https://m.media-amazon.com/images/I/51844dFl3AL.jpg)


