概要
A. Vehtari, Gelman, Simpson, Carpenter, & Bürkner (2020)で提案されているマルコフ連鎖モンテカルロ法(MCMC)の収束確認方法を紹介する. これらはや有効サンプルサイズ(ESS)といった従来よく使われた方法の問題点を解消したものである. 特に重要な, 以下の概念の使い方を紹介する.
正規化ランクと中央値まわりの畳み込み
bulk-ESSとtail-ESS
ランクプロットを始めとする, 上記の視覚化
今回紹介する方法の多くはbayesplotパッケージで用意されている.
これは去年Tokyo.Rの5分間LTやるために書いたものの続きである.
ill-identified.hatenablog.com2021/4/7 追記: この論文は Bayesian Analysis 誌にアクセプトされたらしい (DOI: 10.1214/20-BA1221). 内容は ArXiv のドラフトとほぼ変わっていない.
イントロダクション
実は去年のTokyo.Rの発表の時点でA. Vehtari et al. (2020)による新しい収束チェック方法の提案は公開されていた*1. 蓋を開けてみればどっちにしろ5分間の発表に収まらなかったのだが, この見落としていた内容を今回書いておく. r-wakalangでもここ最近何度かMCMCの収束に関連する質問が投稿されていたので, 収束関係の情報を一箇所に集積しよう*2と思う.
今回書くのはVehtariらの内容ほぼそのままで, 原文はArXivで公開されているし, appendixもオンラインで公開されている.
avehtari.github.ioよって原文を読んだ人にはこのページはほぼ必要なく, またここでは原文を丸写ししたり逐語訳を掲載したりはしないので, より詳しい話は上記を参照してほしい. また一方で, 前回書いたような内容を知らない人は先にそっちを読む必要があるだろう.
今回紹介する方法は, stan, rstanarm, bayesplotなどのパッケージでも既に実装されている方法なので, 結果レポートをどう見ればよいか知らないで使っている人は興味を持ってみると良いかもしれない.
従来の収束チェックの限界
前回にも書いたように, 従来MCMCのサンプル収束はトレースプロットの形状とGelman-Rubin統計量(Gelman & Rubin, 1992, Brooks & Gelman, 1998, Gelman, et al., 2013), いわゆる*3の値が一定以下かどうか確認したり, 有効サンプルサイズ(ESS)が十分大きいかどうかで有効なサンプリング(推定の不確実さを十分に低減できているかどうか)か確認するというやり方が広く普及している.
特にパラメータが膨大な場合は全てのトレースプロットを確認するのは大変なので, だけを確認しがちである. しかし
の値だけであらゆる収束の失敗パターンを排除できているわけではない.
など既存の方法では収束を適切に評価できない場合として, 彼らは以下のような3つの状況を挙げて対処方法を提案している.
系列(連鎖, chains, MCサンプリングの系列データのこと)ごとに分散が大きく異なる場合
期待値が等しくても分散が異なると
は収束していると誤認させる可能性がある
例えば分布のピーク近くの局所解にはまった場合に起こりうる
MCサンプルが裾野の厚い分布(ファットテールな分布, 期待値や分散が有限にならない可能性が高い)となっている場合
連鎖ごとに期待値が異なっていても
は収束していると誤認させる可能性がある
ESSが意味をなさなくなる
そして通常, 分散が有限かどうかをデータから判断するのは困難
標本サイズが十分でない場合
の定義を見れば分かるように, この指標は系列内分散と系列間分散の比率で収束しているかを判定している. 2次モーメント(=分散)のみに依拠しているため各系列の分散が一定で, かつ有限な値に収まることが暗黙の前提となっている. 系列ごとに分散が異なる場合,
の値を過小に見積もり, 誤って収束判定してしまう可能性がある.
 より実践的な収束の判定方法
より実践的な収束の判定方法
以上のように, 収束の失敗のなかにはを見るだけでは発見できないケースが存在する. 彼らは
やトレースプロットよりもより豊富な情報を得られる3つの収束確認方法を提案した.
ランク正規化
系列の
番目のサンプルを
とする.
に対応する, 全系列内での順位を
とする. (タイは平均順位で, いわゆる dense ranking にする?). 以下のようにランク
を正規化した
を正規化ランク (normalized rank, あるいは正規スコア normal scores)と呼ぶ.
は標準正規分布の分位点関数 (分布関数の逆, つまり累積確率に対応する分位点を出力する関数)である. 正規化によって
は元のサンプルとは違って常に正規分布のスケールで表現できるようなり, またランクに変換することで裾野の厚い分布にありがちな外れ値の影響を受けにくくなるとしている. 正規化ランク
で計算した
やESSを, それぞれランク正規化
, bulk-ESSと呼ぶ.
現在のrstanはprint()では従来の計算でとESSを出力するが,
monitor() では bulk-ESSを出力す.
Q5 Q50 Q95 Mean SD Rhat Bulk_ESS Tail_ESS x[1] -7.7 0.0 6.1 -0.5 10.4 1.01 1861 483 x[2] -5.3 0.0 4.6 -0.1 4.5 1.02 3867 1067 x[3] -10.4 0.0 8.4 -7.0 75.4 1.01 969 164 x[4] -4.4 0.0 4.7 0.1 4.5 1.00 4012 967
bulk-ESSは従来のESSと違い元の分布の期待値や分散が有限でなかったり, 系列ごとに分布の中央値が異なっていても意味をなす. なお, bulk-ESSは2次モーメントの収束を見るためのものだが, ランク正規化してしまったことによりbulk-ESSからモンテカルロ標準誤差(MCSE)を計算することはできなくなっている.
ランクプロット
正規化ランクを使った, トレースプロットに対応する視覚化方法であるランクプロットが提案されている. ランクプロットは系列ごとに正規化ランクのヒストグラムを描いたものである. トレースプロットではサンプルが期待値から大きく外れているとき(比較的初期の収束していない状態や, 分散の大きい事後分布)に見づらいが, ランクプロットはランク正規化によってスケール変換されているためそのような場合でも見やすくなっている. サンプルが適切に収束しているならヒストグラムは一様分布に近づき, 逆に系列が異なる期待値や分散に収束すると一様分布の形状からずれた不均一なものになる.
具体的な例として, コーシー分布(自由度1のt分布)のサンプリングを挙げる (と言ってもappendixで掲載されているものをさらに簡略化しただけだが). コーシー分布は平均も分散も有限値に収束しないことが知られているのでうってつけの例である.
require(conflicted) require(tidyverse) require(ggthemes) require(rstan) require(bayesplot) conflict_prefer("extract", "rstan") conflict_prefer("filter", "dplyr") conflict_prefer("lag", "dplyr") conflict_prefer("Position", "ggplot2") rstan_options(auto_write = TRUE) options(mc.cores = parallel::detectCores()) theme_set(theme_classic(base_size=18, base_family = "Noto Sans CJK JP")) stan_cauchy <- " parameters { vector[50] x; } model { x ~ cauchy(0, 1); } generated quantities { real I = fabs(x[1]) < 1 ? 1 : 0; } " model1 <- stan_model(model_code = stan_cauchy) sample1 <- sampling(model1, seed=42)
sample1がサンプリング結果である. 最初の4つのパラメータ x[1] から x[4] までを抜粋する(図1).
print(sample1) mcmc_rhat(rhat(sample1, pars = paste0("x[", 1:4, "]"))) + scale_color_colorblind() + theme(axis.text.y = element_text())</code></pre> >|| mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat x[1] -0.45 0.40 10.40 -15.68 -1.10 -0.03 0.99 11.12 675 1.01 x[2] -0.14 0.09 4.49 -8.83 -1.01 -0.03 0.94 7.47 2538 1.00 x[3] -7.02 7.27 75.38 -32.41 -1.03 0.00 1.04 18.56 108 1.04 x[4] 0.13 0.10 4.52 -7.33 -0.94 0.01 0.93 8.13 2145 1.00

の抜粋
いずれもの値は十分小さいので収束しているかに見える. しかしESSの値が不揃いなのが少し怪しい. というわけで早速ランクプロットを試してみる.
bayesplot()パッケージには, mcmc_rank_hist(), mcmc_rank_overlay() という2つの関数が用意されている. 前者は個別のヒストグラムを描画し, 後者は名前通り各系列のランクプロットを重ねて表示する(図2, 図3).
mcmc_rank_hist(as.array(sample1), pars = paste0("x[", 1:4, "]"))

code>mcmc_rank_hist()の描画例
mcmc_rank_overlay(as.array(sample1), pars = paste0("x[", 1:4, "]")) + scale_color_colorblind()

mcmc_rank_overlay()の描画例
たしかにヒストグラムは一様というより裾野で不自然に頻度が高まっているものがいくつか見られる. これを従来のトレースプロットで確認してみる(図4).
mcmc_trace(ar_sample1, pars = pars) + scale_color_colorblind()

トレースプロットでもときどきサンプルが大きく振れ動くことがあるのが分かるが, 外れ値が大きすぎて他のサンプルがどれくらいランダムなのかはわかりづらい.
補足: コーシー分布をどう収束させるか
では, このようなモデルのサンプリングをどう収束させるかというと, 論文では次のような再パラメータ化が提案されている.
このはガンマ分布を表す.
をいきなりコーシー分布からサンプリングするのではなく, 正規分布とガンマ分布の乱数
から計算する. この2つの分布はどちらも分散が有限でありコーシー分布ほど裾野が厚くないが,
と変換するとコーシー分布と等価になる.
(これはコーシー分布が自由度1のt分布と等しいこと, 自由度のt分布の確率変数が正規分布を自由度
のカイ2乗分布の確率変数で除したものの分布と等しいこと, そして自由度
のカイ2乗分布がパラメータ
のガンマ分布と等しいという統計学の教科書にもよく載っている事実から分かる)
この方法でやり直した結果, は全て1.01以下となった.
Q5 Q50 Q95 Mean SD Rhat Bulk_ESS Tail_ESS x_a[1] 0.07 0.70 1.96 8.100000e-01 6.000000e-01 1.00 2655 1569 x_a[2] 0.06 0.67 1.97 7.900000e-01 6.100000e-01 1.00 2594 1683 x_a[3] 0.07 0.70 1.95 8.100000e-01 6.000000e-01 1.00 3347 1694 x_a[4] 0.07 0.67 1.93 8.000000e-01 6.000000e-01 1.00 2660 1397
再びランクプロットとトレースプロットで表すと以下のようになる(図5, 図6). x[3]の系列3の裾野のサンプリングが改善されていることがわかるが, トレースプロットではこのことは分かりにくい.


中央値まわりの畳み込み
期待値の収束を見るためのはサンプルを正規化ランクに置き換えることでより使いやすいものとなった. しかし正規化ランクでは2次モーメントの評価はできない. 標準誤差の計算をしても元のサンプルの標準誤差を反映できない. また, 平均は一致しても分散が一致しないようなケースでは正規化ランク
でも意味をなさない. その場合, サンプルの中央値まわりの畳み込み (以下, 単に「畳み込み」という)をすることが提案されている. 畳み込みと書くとわかりづらいかもしれないが, 以下のように中央値からの偏差の絶対値を取っただけである.
従来のだけでなく, ランク正規化
や畳み込みしてからランク正規化したランク正規化畳み込み
を使う.
ここまでの方法のまとめ
ランク正規化と畳み込みでを計算した場合, どう違いが発生するのかを実験してみる. ヘルプによると
rstan::Rhat() (rhat()ではない)は, 通常の, ランク正規化
, ランク正規化畳み込み
のうち最大の値を
として出力することができるが, どれを出力するかは指定できない. ランク正規化も畳み込みも実装は簡単だが, 著者の1人であるVehtariの書いた
monitornew.Rにはそれぞれを出力する関数が定義されているのでこれを使う.
の計算はモンテカルロ法を1度実行するたびに行うので, 同じモンテカルロ法の計算を乱数だけ変えて何度も繰り返して得た
の分布を確認することになる. いわばモンテカルロ法のモンテカルロシミュレーションである. ただし単純なモデルでもstanを数千回も実行するのは時間がかかるので, 手抜きして単純に独立な乱数を発生させてシミュレーションしてみた. とはいえモンテカルロ法の究極の目的は独立な乱数による事後分布の近似なので, これで
が適切に機能しないというのなら完全には独立でないMCMCではなおさらうまくいかないだろう. サンプリング数は
, 系列数は
として, 論文と同じように1000回
の計算を繰り返した結果をヒストグラムで表す.
位置シフトと分散の不均一さはそれぞれというパラメータで表現し, それぞれ正規分布とカイ2乗乱数で適当に決めた. 分散や平均が有限でない乱数はt分布を使った. t分布は自由度1のとき(=コーシー分布)平均も分散も存在せず, 自由度2のとき平均は収束するが分散は無限大になり, 自由度3以上では分散も収束する. 一方でどの自由度でも常に中央値を定義できる. 具体的にはそれぞれ以下表1のような分布に基づいて乱数を生成した.
| 平均値 | 位置シフト | 分散 | 分布 |
|---|---|---|---|
| あり | なし | 均一 | |
| あり | なし | 不均一 | |
| あり | なし | ||
| あり | あり | 均一 | |
| あり | あり | 不均一 | |
| あり | あり | ||
| なし | なし | ||
| なし | あり |
その結果が図7である.
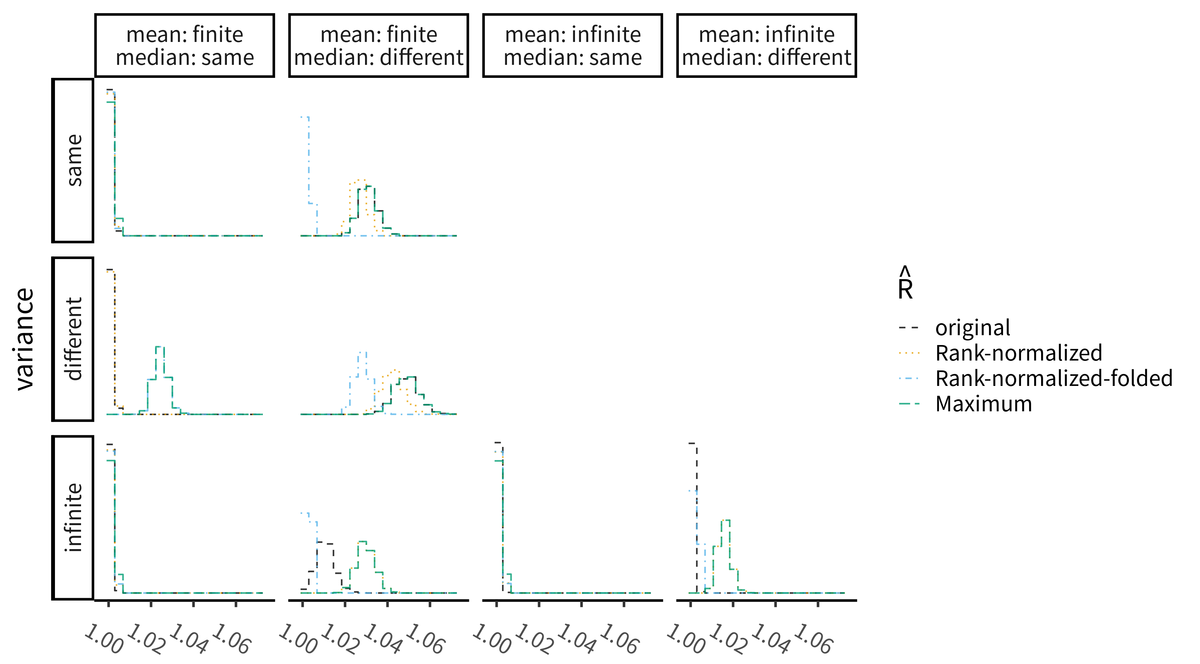
の挙動の違い
論文の Fig. 1 との違いは, 平均値が異なる場合の挙動とも比較している点である. ここまで書いたように, 分散が無限大(infinite, 下段)の場合ははランク正規化したほうが値が大きくなり, 収束したと判断されづらいことが分かる. 一方で, 平均が一定かつ分散が不均一(different, 中段)な場合はランク正規化も通常の
と大差なく, 上記のように畳み込み変換も必要になってくる. しかし, 畳み込みは中央値で中心化しているために系列ごとに中央値の位置が異なる場合(different, 左から第2列)にその情報が欠落してしまうため, 収束したと誤認してしまうことがある. よって, ランク正規化と畳み込みはそれぞれあらゆる問題を検知できるわけではなく, 相変わらず何らかの弱点が存在するため, これら3種類の
の最大値(図中の "maximum")に注意すべきというVehrariらの主張が理解できる.
tail-ESSと分位点の推定
とESSは分布全体での収束を診断するための指標だったが, 今回例にしたコーシー分布のように, 分布の裾野だけ効率よくサンプリングできないというケースもある. 統計モデリングでは点推定(多くは平均値の推定)だけでなく, 信頼区間を知りたい場合もあるため, 分布の局所的な箇所でのサンプリングを診断する方法が必要になる. そこで, tail-ESSというものを考案している
分位点のうち, 分布の両端付近が特に重要であることが多い. 特に 5%, 95%分位点でのESSを tail-ESSと呼ぶ. (どのような分位点でも計算できるが, 特に理由がないなら信頼区間のように5%, 95%分位点で計算すると分かりやすいだろう.) 分位点なので系列ごとのスケールの違いに依存しないという利点がある.
また, 既に述べたように, 周辺事後分布の平均や分散は有限でないかもしれない. そのような場合は中央値や絶対中央偏差 (MAD) を確認することも重要であり, rstanarmパッケージでも既にこれを出力する機能がある*4 (ご存知のように中央値は50%分位点と同じなので, 上記の方法で推定できる).
ローカルESSプロット
ESSやbulk-ESSはサンプル全体を評価したものであるが, 全体のESSと局所的なESSは大きく異なる場合がある. そこで, 分位点の推定をしたい場合は特に, サンプルを分位点で見て等間隔で分割し, それぞれの区間のESSをプロットして確認することが重要になる.
この結果, ビンが低い区間ほどESSが小さく, 不確実さが大きいと判断できる.
あるいは逆に, 分位点で分割することで, 各区間のサンプルサイズを等しくする方法も考えられる.
bayesplotにはまだ対応する機能がないが, 近いうちに実装されるようだ*5. 今回はVehtariの開発中のコードmonitorplot.Rにある plot_local_ess()とplot_quantile_ess()を使う. 現時点ではそれぞれ1つのパラメータに対してのプロットしかできないようだ.
source("monitorplot.R") plot_local_ess(ar_sample1, par = "x[1]") + scale_color_pander() plot_quantile_ess(ar_sample1, par = "x[1]") + scale_color_pander()
結果は以下の図8の通り. デフォルトでは bulk-ESSが計算される.


上下の図ともにy軸がbulk-ESSで, 区切り方が異なる. どちらからも裾野のサンプリングが特に少ないとわかる. 破線は推奨される最低限必要なESSの大きさで, 今回のサンプリング回数では400になる.
時系列ESSプロット
bulk-ESSでもtail-ESSでもサンプルサイズが小さいうちはあまり当てにならない. そこで, サンプリング回数に対応したbulk/tail-ESSを計算して推移をプロットすることで, 低速混合の発生を見つけられることがある. 例えば, bulk-ESSは順調に上昇してtail-ESSが上昇しない場合は低速混合の可能性がある. 既に紹介したランクプロットはトレースプロットと比較して紹介したが, ランクプロットはヒストグラムなのでトレースプロットでは読み取れた時系列的な変化が読み取れなくなっている.
これもbayesplotにはまだ用意されてないので, やはりmonitorplot.Rのplot_change_ess()を使う.


図9の上段ではy軸のスケールを absolute に, 下段 “relative“ に設定している. 前者はそのままだが, 後者はESSをサンプリング数で割った値を表示している. この図からも裾野のサンプリングが不十分であることが読み取れる.
まとめ
Vehtariらによって提案されたアイディアの肝は, モンテカルロサンプルに以下の2種類の変換を施すことである- ランク正規化により分布の裾野の厚い分布から多く発生する外れ値に影響を受けにくくなる
- 中央値まわりの畳み込みによって, 系列ごとの分散の異質性を検知しやすくなる
参考文献
- Brooks, S. P., & Gelman, A. (1998). General methods for monitoring convergence of iterative simulations. Journal of Computational and Graphical Statistics, 7(4), 434–455. doi:10.2307/1390675
- Gelman, A., & Rubin, D. B. (1992). Inference from Iterative Simulation Using Multiple Sequences. Statistical Science, 7(4), 457–472. doi:10.1214/ss/1177011136
- Gelman, A., Carlin, J. B., Stern, H. S., Dunson, D. B., Vehtari, A., & Rubin, D. B. (2013). Bayesian Data Analysis (3rd ed.). CRC Press.
- Vehtari, A., Gelman, A., Simpson, D., Carpenter, B., & Bürkner, P.-C. (2020, January). Rank-normalization, folding, and localization: An improved
for assessing convergence of MCMC. arXiv: 1903.08008
*1:2020年に更新されているが, 初出は2019年3月である.
*2:なお, 前回の記事の冒頭では「日本語でも英語でも収束判定に関する実用的な情報が不足している」と書いていたが, 現在は stanの公式ページを中心に少しづつ英語ドキュメントが充実しつつある.
*3:以降では, 単にといえば原則として各系列を前後で分割して別々の系列として計算する分割
を前提とする. 分割
は通常の
と比べて系列ごとの収束を確認しやすいからである.
*4:私は使ったことがないので未確認
*5:Local ESS, quantile ESS, ESS change, and rank-based alternative to traceplot · Issue #178 · stan-dev/bayesplot · GitHub. また, Gelman のブログによれば stan とその派生パッケージでも実装する予定らしい: https://statmodeling.stat.columbia.edu/2019/03/19/maybe-its-time-to-let-the-old-ways-die-or-we-broke-r-hat-so-now-we-have-to-fix-it/
