互いに独立でなくてもできる中心極限定理と, そのデモ (Gordin's CLT/Donsker定理)

概要
はじめに
シミュレーション
統計学への応用
- 相関ありの中心極限定理の応用
- 汎関数中心極限定理の応用
参考文献

概要

今月まだ何も書いてなかったのでタイトルの通り中心極限定理の発展的な話をする. といってもAR(1)とランダムウォーク乱数のグラフを描いただけなんだけど.

対象読者: 統計学の入門的な教科書に書いてある中心極限定理 (CLT) や大数の法則は知っているが, そこから先は知らない人

はじめに

ほとんどの基礎的な教科書に書いてある回帰分析や機械学習のモデルではデータが互いに独立かつ同一の分布 (IID) であると仮定している. これは大数の法則や中心極限定理が成り立つ条件の1つでもあり, よって十分にデータが多ければ, 大数の法則により推定した係数が正しい値にうまく収束しているとか, 中心極限定理から導かれる確率分布に基づいて, 区間推定や仮説検定ができるという根拠になっている.

いちおう数式を掲載しよう. $\{Y_1, Y_2, \cdots\}$ という互いに独立な確率変数列があり, それぞれ期待値が同一の $\mu$ , 分散が有限かつ一定な $\sigma^2$ であるとする. その部分標本平均を $\bar{Y}_N:=(1/N)\sum_{i=1}^NY_i$ と書くと, $N\to\infty$ のときに $\bar{Y}_N$ が正規分布に弱収束することを中心極限定理は示している.

$\begin{align} \frac{(\bar{Y}_N -\mu)}{\sigma/\sqrt{N}} \underrightarrow{d} \mathcal{N}(0,1)\end{align}$

また, 大数の(強)法則は, 同様の条件のもとで, $\bar{Y}_N$ が $\mu$ に強収束 (別名, 概収束) することを表している. 多くの教科書ではこのように紹介されている.

機械学習の教科書では区間推定や仮説検定が取り上げられることはまれなので, これらの定理も紹介される事があまりない. しかし機械学習では不要ということは全くなく, ほとんどの教科書や論文では「データのインスタンスが互いに独立かつ同一の分布である」というような仮定が書いてあるはずだ. これは暗に, 上記のような定理の性質が良い予測モデルを得るために必要な条件になっていることを意味する.

では, これらの前提である, 「互いに独立」はいつでも成り立つのだろうか? たとえば, 毎日の観測, あるいは1時間ごとの観測を記録した時系列データではどうだろうか. 昨日と今日のあなたの体重, あるいは今と1時間前の気温は本当に独立と言えるだろうか?

そこで, IID な乱数列と, 互いに独立ではない時系列データの例として, 安定な1階の自己回帰過程 (AR(1))とランダムウォークの時系列 $\{Y_t\}_{t=1}^N$ でそれぞれシミュレーションをしてみる.

AR(1) は,

$\begin{align} Y_t &= \rho Y_{t-1} + \varepsilon_t, |\rho|<1\end{align}$

のように1つ前の値に依存する確率変数列であり, ランダムウォークは, 互いに独立な正規乱数 $\varepsilon_t$ の累積で表される.

$\begin{align} Y_t &= \sum_{s=1}^t \varepsilon_t\end{align}$

これら2つの時系列 $\{Y_t\}$ は明らかに過去の値と相関を持つため, 互いに独立ではない.

シミュレーション

今回は $N=500$ の乱数列を, $M=500$ 個並列して作成することで, 3つのケースでの標本平均 $\bar{Y}_N$ の収束と分布を確認する. どれも期待値ゼロなので, ゼロ周辺に収束しているかが確認できればよい.

require(tidyverse)
require(ggthemes)
require(hrbrthemes)
require(broom)
theme_set(theme_ipsum_rc(base_family = "Noto Sans CJK JP") + theme(legend.position = "none"))
thm_hist <- theme(axis.title.y = element_blank(),
      axis.text.y = element_blank(),
      axis.ticks.y = element_blank())
update_geom_defaults("line", list(color = "steelblue"))

## Loading required package: tidyverse
## -- Attaching packages --------------------------------------- tidyverse 1.3.0 --
## v ggplot2 3.3.3     v purrr   0.3.4
## v tibble  3.0.6     v dplyr   1.0.4
## v tidyr   1.1.2     v stringr 1.4.0
## v readr   1.4.0     v forcats 0.5.1
## -- Conflicts ------------------------------------------ tidyverse_conflicts() --
## x dplyr::filter() masks stats::filter()
## x dplyr::lag()    masks stats::lag()
## Loading required package: ggthemes
## Loading required package: hrbrthemes
## NOTE: Either Arial Narrow or Roboto Condensed fonts are required to use these themes.
##       Please use hrbrthemes::import_roboto_condensed() to install Roboto Condensed and
##       if Arial Narrow is not on your system, please see https://bit.ly/arialnarrow
## Loading required package: broom

N <- 500
M <- 500
set.seed(42)
d_iid <- map_dfr(1:M, ~tibble(t = 1:N, series = .x, y = rnorm(n = N)))
d_ar1 <- map_dfr(1:M, ~tibble(t = 1:N, series = .x,
                              y = arima.sim(model = list(order = c(1,0,0), ar = .6), n = N)))
d_rw <- map_dfr(1:M, ~tibble(t = 1:N, series = .x, y = cumsum(rnorm(n = N))))

IIDな時系列 (基本)

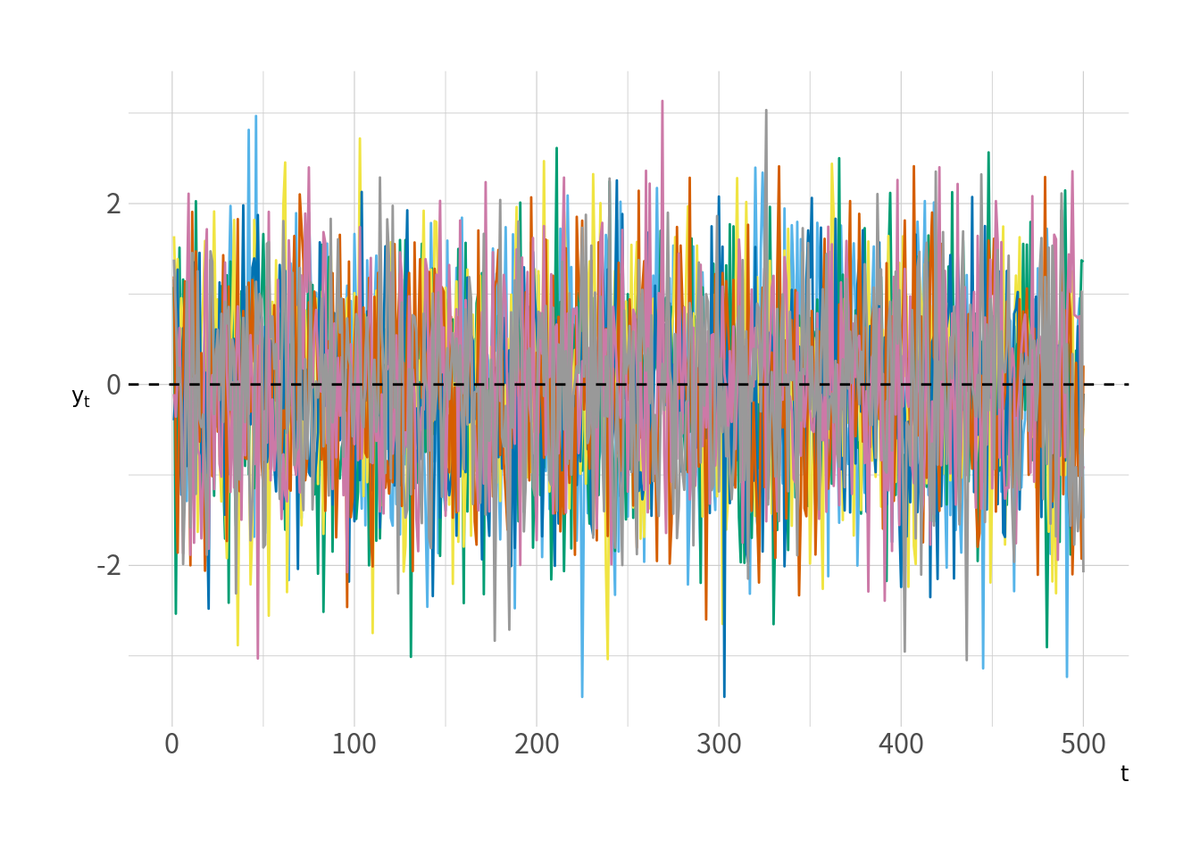
まずは図1に IID な乱数の原系列のうち, 7系列をプロットする. 完全に独立なので MCMC がうまく計算できたときのトレースプロットのような見た目になっている.

ggplot(d_iid %>% filter(series %in% sample(1:M, 7)),
       aes(x = t, y = y, group = factor(series), color = factor(series))) +
  geom_line() + geom_hline(yintercept = 0, linetype = 2) +
  labs(y = expression(y[t])) +
  scale_color_pander()

f:id:ill-identified:20210331203743p:plain — 図 1: IIDの原系列7つ

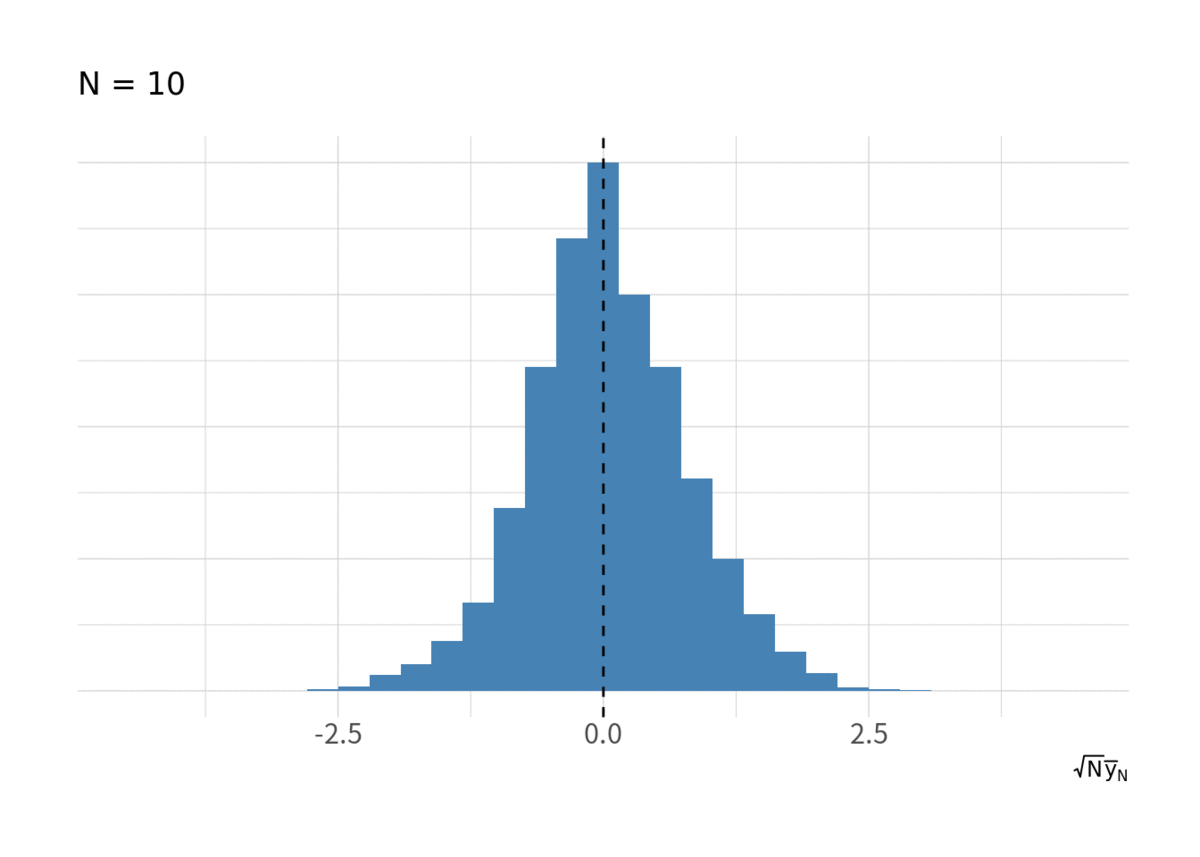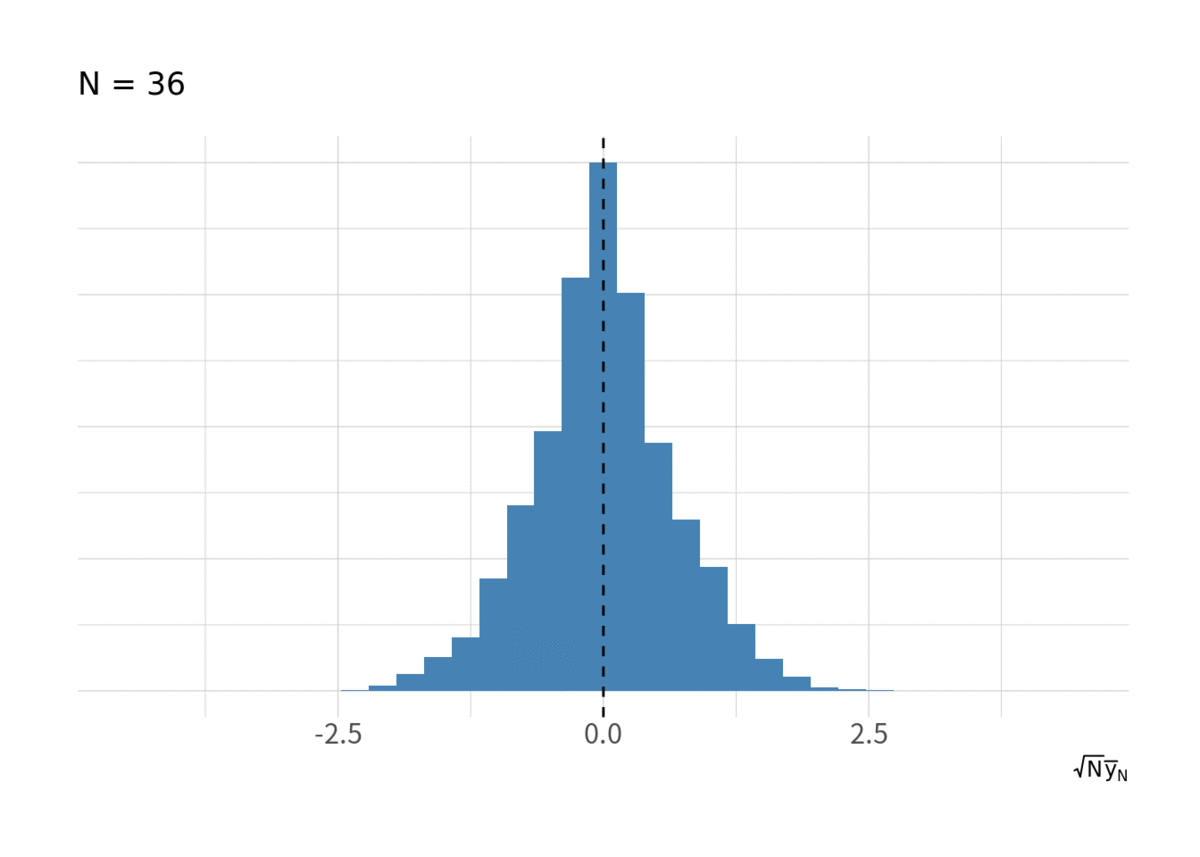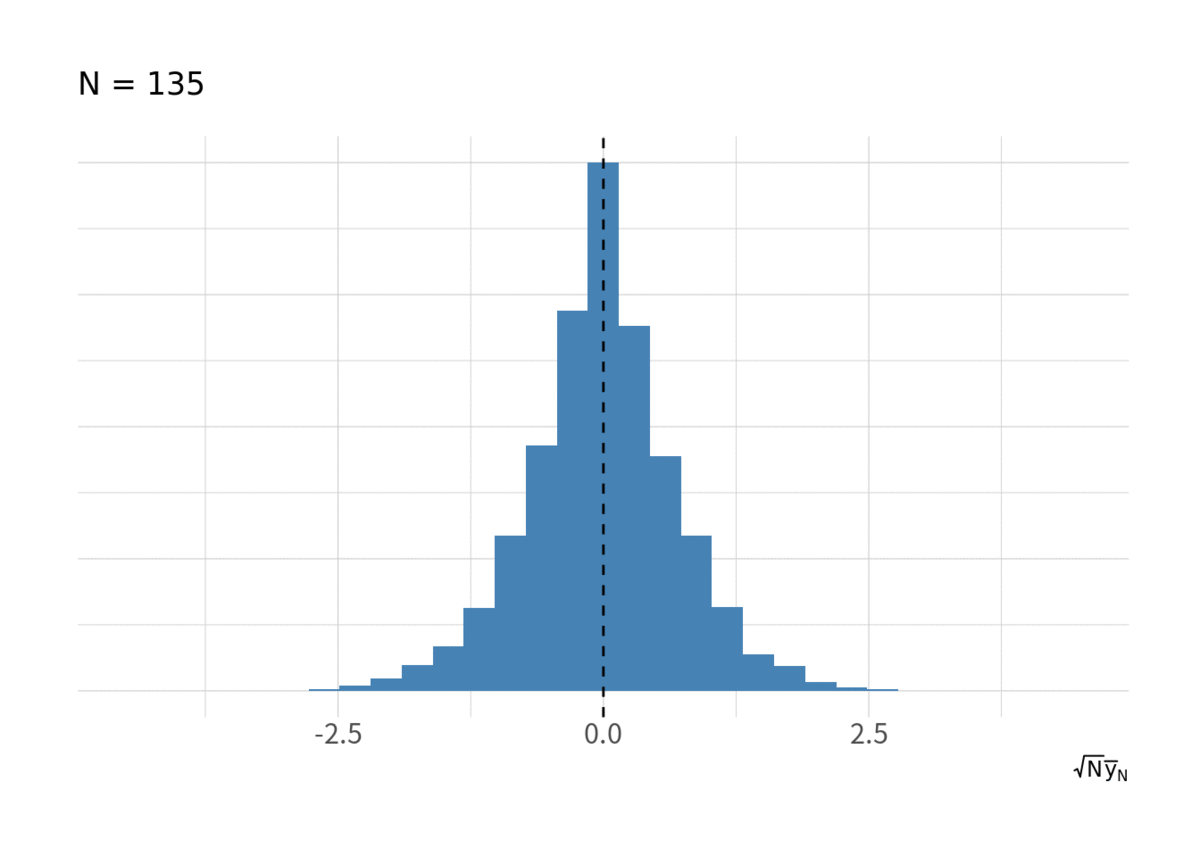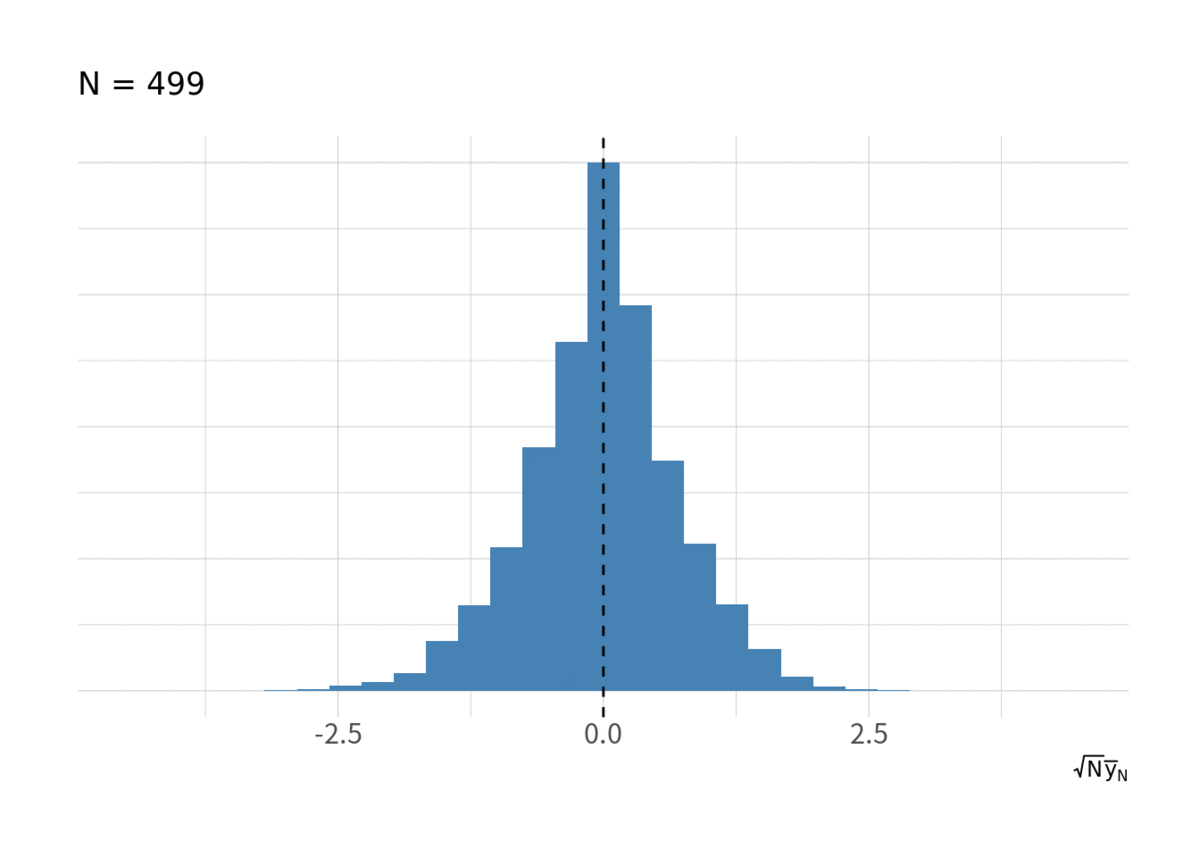
IIDな乱数の標本平均列 $\bar{Y}_N$ が正規分布に収束する様子はいろんなところで見てきたかもしれないが, 一応. 図2が $N$ が増大したときの $\sqrt{N}\bar{Y}_N$ のヒストグラム.

f:id:ill-identified:20210331204009g:plain — 図 2: IIDな時系列の $\sqrt{N}\bar{Y}_N$ のヒストグラム

for(i in floor(exp(seq(log(10), log(N), length.out = 10)))){
  g <- d_iid %>% filter(t < i) %>% group_by(series) %>%
    summarise(ybar = sqrt(t) * mean(y), .groups = "drop") %>%
    ggplot(aes(x = ybar, y = stat(ndensity))) +
    geom_histogram(bins = 20, fill = "steelblue") + geom_vline(xintercept = 0, linetype = 2) +
    labs(x = expression(sqrt(N) * bar(y)[N]), subtitle = paste("N =", i)) +
    coord_cartesian(xlim = c(-4.5, 4.5)) + thm_hist
  print(g)
}

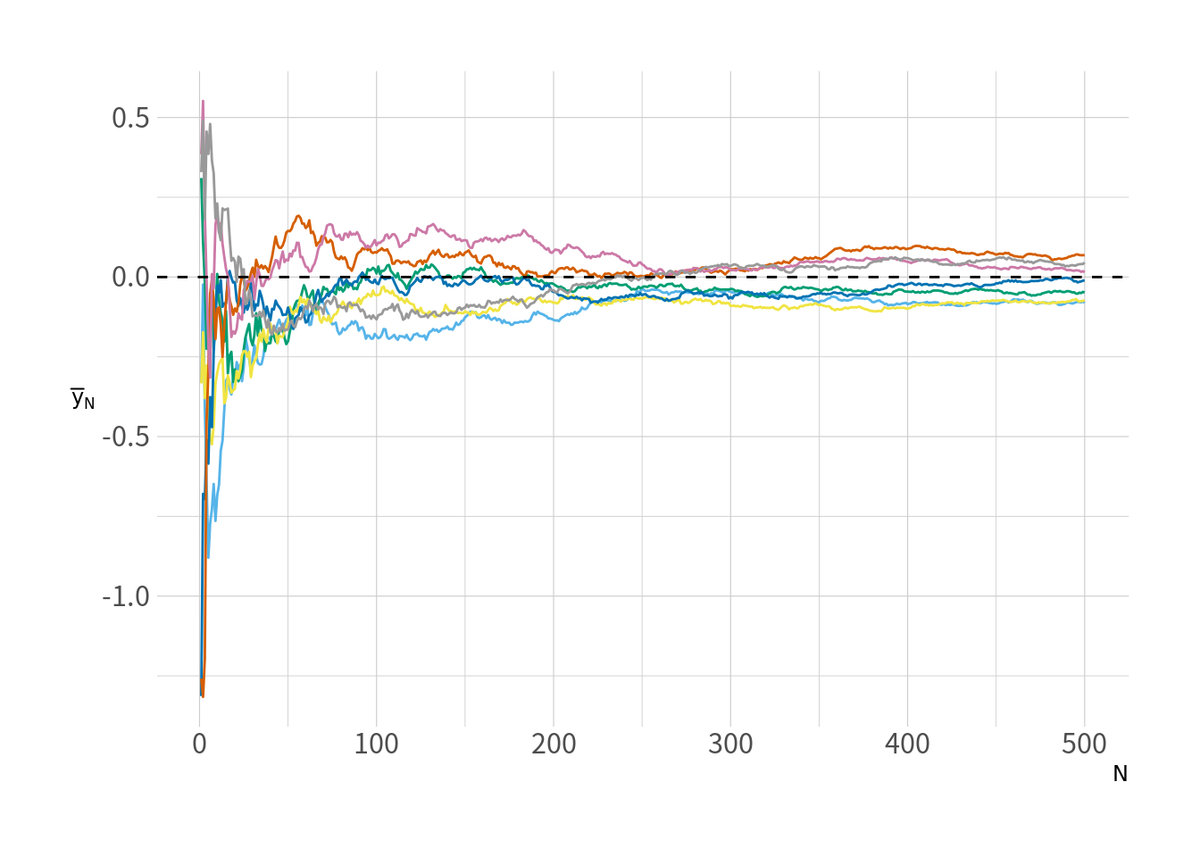
そして $N$ の増加に従って標本平均 $\bar{Y}_N$ が収束していくのが図3.

d_iid %>% filter(series %in% sample(1:M, 7)) %>%
  group_by(series) %>% mutate(y = cummean(y)) %>% ungroup %>%
  ggplot(aes(x = t, y = y, group = factor(series), color = factor(series))) +
  geom_line() + geom_hline(yintercept = 0, linetype = 2) +
  labs(x = expression(N), y = expression(bar(y)[N])) +
  scale_color_pander()

f:id:ill-identified:20210331203820p:plain — 図 3: IID な乱数7系列の標本平均の収束

独立ではないケース1: AR(1)

原系列は図4. 特に面白いこともない. さっきの図1と比べてなんか相関してるような見た目に見えることだろう.

ggplot(d_ar1 %>% filter(series %in% sample(1:M, 7)),
       aes(x = t, y = y, group = factor(series), color = factor(series))) +
  geom_line() + geom_hline(yintercept = 0, linetype = 2) +
  labs(y = expression(y[t])) + scale_color_pander()

f:id:ill-identified:20210331204332p:plain — 図 4: AR(1)の原系列7つ

図5 も IID の場合とよく似ている.

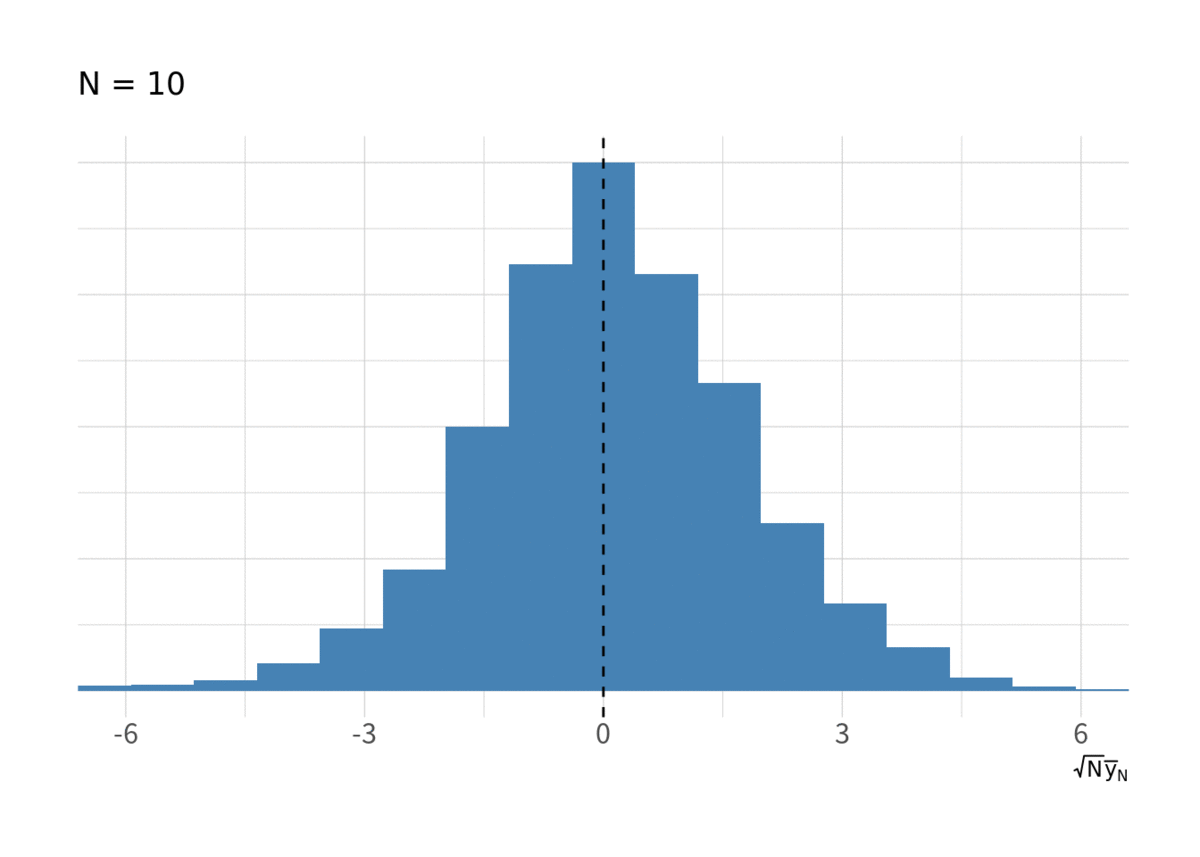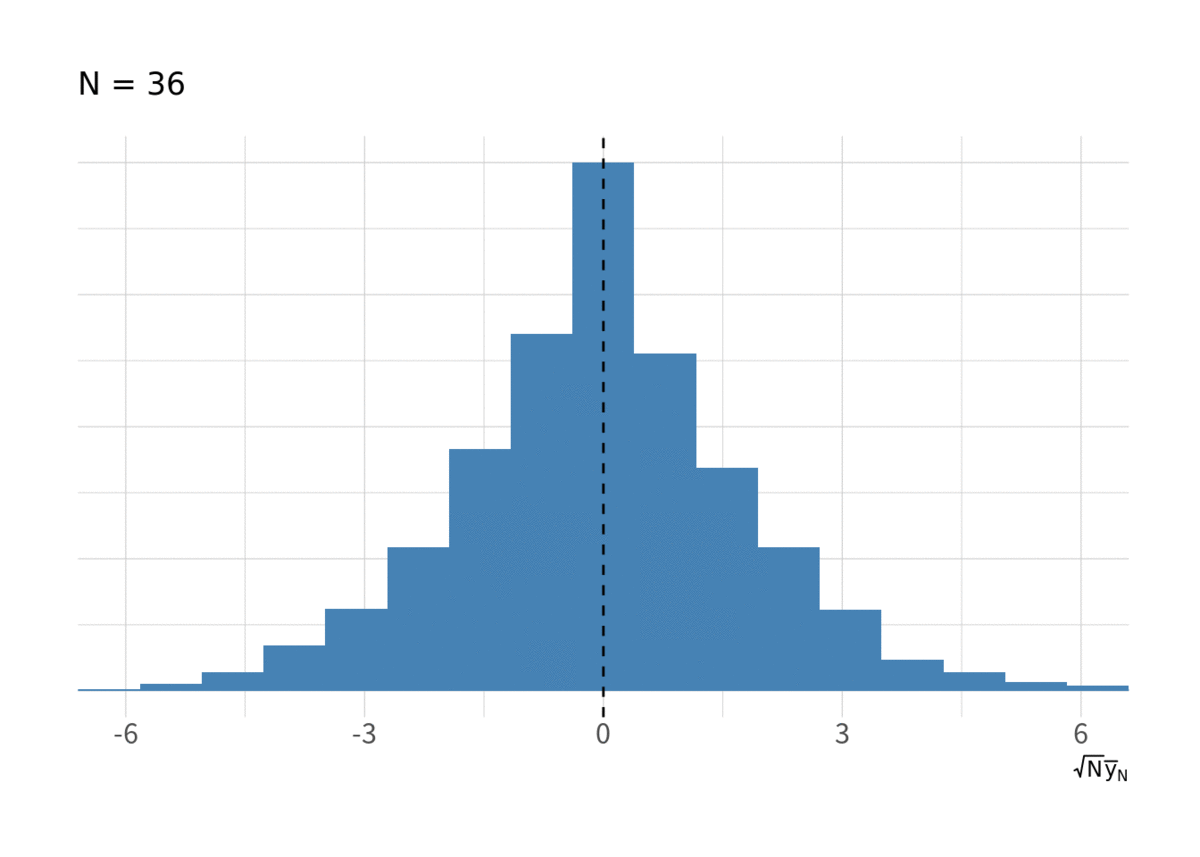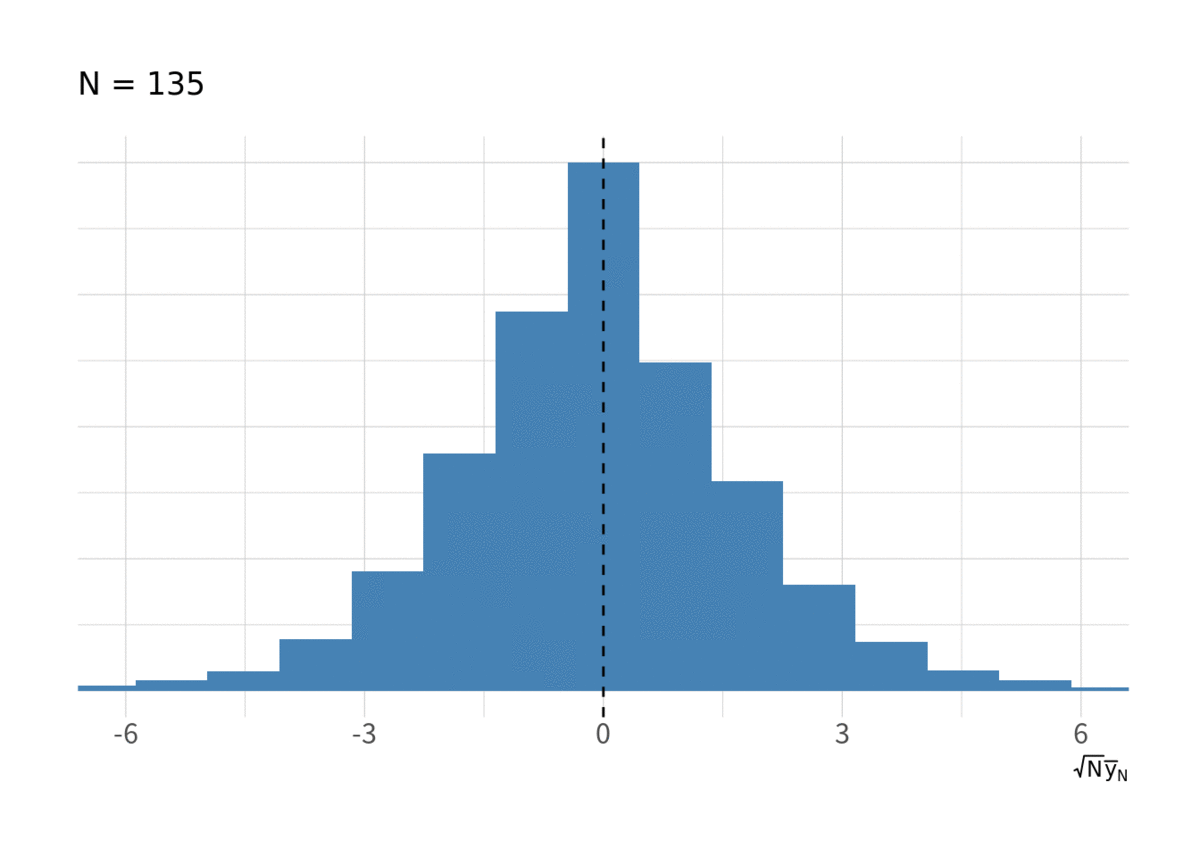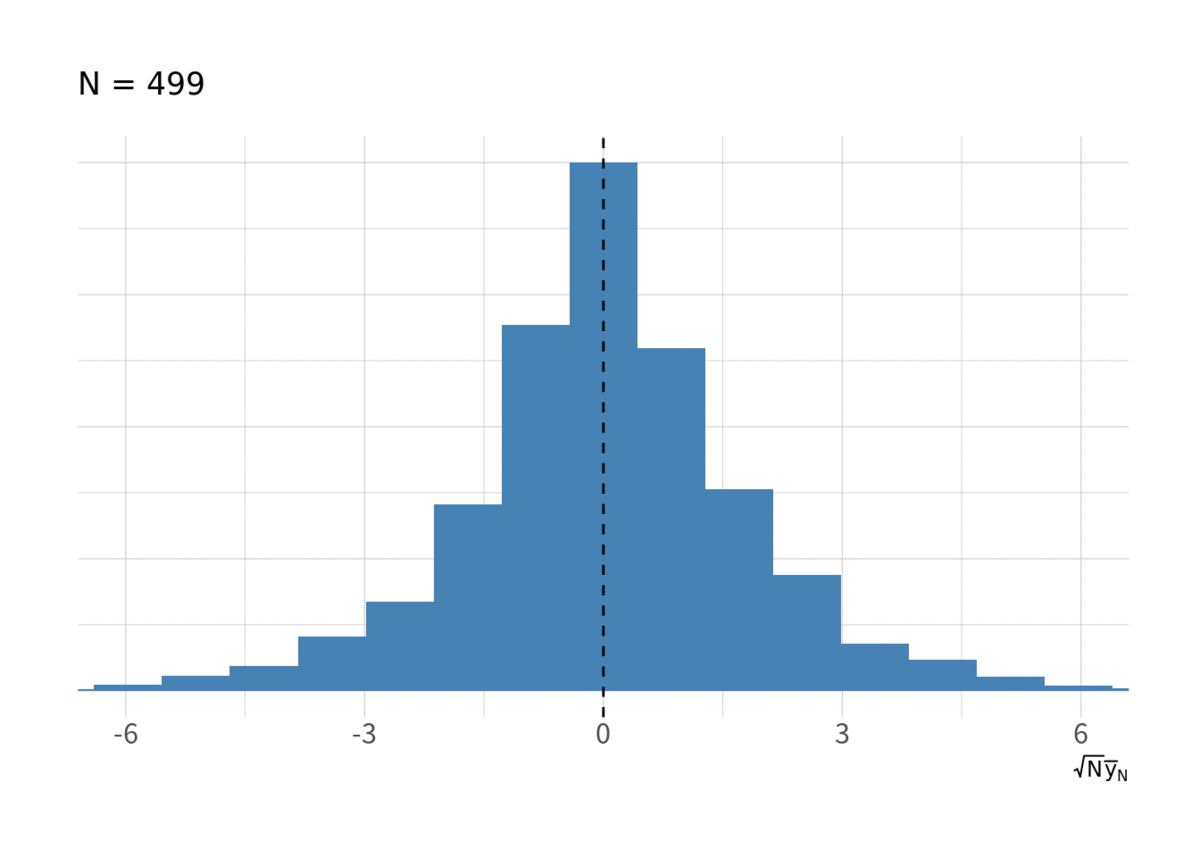
f:id:ill-identified:20210331204345g:plain — 図 5: AR(1) 時系列の $\sqrt{N}\bar{Y}_N$ のヒストグラム

for(i in floor(exp(seq(log(10), log(N), length.out = 10)))){
  g <- d_ar1 %>% filter(t < i) %>%
    group_by(series) %>% summarise(ybar = sqrt(t) * mean(y), .groups = "drop") %>%
    ggplot(aes(x = ybar, y = stat(ndensity))) +
    geom_histogram(bins = 20, fill = "steelblue") + geom_vline(xintercept = 0, linetype = 2) +
    labs(x = expression(sqrt(N) * bar(y)[N]), subtitle = paste("N =", i)) +
    coord_cartesian(xlim = c(-6, 6)) + thm_hist
  print(g)
}

標本平均と $N$ の関係が図6.

d_ar1 %>% filter(series %in% sample(1:M, 7)) %>%
  group_by(series) %>% mutate(y_bar = cummean(y)) %>% ungroup %>%
  ggplot(aes(x = t, y = y_bar, group = factor(series), color = factor(series))) + geom_line() +
  geom_hline(yintercept = 0, linetype = 2) +
  labs(x = expression(N), y = expression(bar(y)[N])) +
  scale_color_pander()

f:id:ill-identified:20210331204644p:plain — 図 6: AR(1) 7系列の平均の収束

これもどうやら収束しているようである. AR (1) は冒頭の「互いに独立」を明らかに満たさないが, 実は中心極限定理 (CLT) の条件にはいくつもバリエーションがある. よく教科書に載っているものは「Lindeberg-Lévy の CLT」と呼ばれるタイプで, これは最も古典的で証明が簡単なので教科書に載っているが, 条件が最も厳しい. より条件を緩めたのものの1つが「Gordin の CLT」および「弱定常LLN」と呼ばれる定理で, このように AR(1) でも収束することが示唆されている. ただし AR(1) ならなんでも成り立つわけではなく一定の条件 (安定性条件) が必要で, 漸近分布の分散も長期的な分散と共分散の和に依存したものになる. 詳細は Hayashi (2000) Ch. 6 か White (2001) Ch. 5*1 を参照してほしい*2. あと手元にないので確認できないが, Hamilton の “Time Series Analysis” にも書いてあったと思う.

2022/1/17 追記: 英語版Wikipediaにマルコフ連鎖中心極限定理という記事があるのを見つけた. 表現に一部曖昧なところがあるが, マルコフ連鎖列に対する中心極限定理であり, マルコフ連鎖は一般に強定常性の条件は満たせないが弱定常は条件の追加で満たすことができるので, おそらく Gordin の中心極限定理と似たような応用を想定した定理だと思う. 参考文献にも Gordin という著者の論文が引用されている (内容は未確認) ので, この名前で探したほうが情報収集しやすいかもしれない. しかし日本語のページではこれに言及しているものは全然見当たらない (Wikipedia のこの記事を機械翻訳するサイトがいくらか見つかる程度)

2022/1/17 追記: マルチンゲール差分列の中心極限定理

一番仮定のゆるい Gordin のCLT だけ紹介すれば, IID でなくとも定常時系列全般で中心極限定理を使えるということがわかるのでこれだけ紹介したが, 心変わりしたので「マルチンゲール差分列のCLT」も簡単に紹介しておく. こちらは Gordin よりも仮定が厳しいので AR(1) の分布収束に適用することはできないが, Lindeberg-Lévy よりはいくぶん「現実味」がある条件に思えるため, IIDの条件に納得できない人は調べてみるといいかもしれない. これも Hayashi (2000) の Ch. 3 に解説がある. (定常性の定義とかもこの章に書いてあるので問題のセットアップとして読むといい)

簡潔に言えば, 名前が示すとおり, ${Y_t}$ が IID でなくともマルチンゲール差分列でかつ分散が有限ならば, $\sqrt{N}\bar{Y}_N$ が $N$ の増大に対してやはり正規分布に収束するという定理である. マルチンゲール差分列は (強い定常性を要求するので) 系列相関を許容せず, AR(1) はこの定理の条件を満たさない. また「マルチンゲール」と「マルチンゲール差分列」は異なることに注意. 例えばこのあと見ることになるランダムウォークはマルチンゲールだが, マルチンゲール差分列ではないため, この定理を適用できない. 参考にした本では「マルチンゲール差分列の中心極限定理」と表現されているが, 日本語の資料ではなぜか「マルチンゲール中心極限定理」と表記されていることが多く, 紛らわしいので注意. (たとえば西山陽一先生の資料: https://ibisml.org/ibis2010/session/ibis2010nishiyama.pdf もちろんこの表記とは関係なく, 資料として良い.) また, マルチンゲール差分列であることはその数列がエルゴード定常であることを意味するため, エルゴード定理により平均値はある値に収束する. よって大数の法則に対応する定理も存在する.

すごく大雑把な表現をすれば, マルチンゲール差分列のCLTは「確率変数列が互いに独立でなくとも, 長期的に見て, 安定した性質を持っている確率分布ならば中心極限定理や大数の法則を適用できる, しかし AR(1) のように自己相関がある場合まではカバーできない」ということを意味している. (この「安定した性質」という表現では何も言っていないような説明になってしまっているが、色々な用語の定義を導入せずに説明するのは難しい。これが具体的になんなのかは参考文献を読んでほしい)

独立ではないケース2: ランダムウォーク

安定的な AR(1) のように, 一定の条件を満たす時系列データであれば, 互いに独立でなくても CLT が成り立つ事がわかった. ではランダムウォークについてはどうか. AR(1) のように, 確率変数の線形和だから同じような結果になりそうだと思うだろうか? 図7が原系列.

ggplot(d_rw %>% filter(series %in% sample(1:M, 7)),
       aes(x = t, y = y, group = factor(series), color = factor(series))) +
  geom_line() + geom_hline(yintercept = 0, linetype = 2) +
  labs(y = expression(y[t])) + scale_color_pander()

f:id:ill-identified:20210331204733p:plain — 図 7: ランダムウォークの原系列7つ

次に, ちゃんと正規分布になっているかを見る. まずは図8のヒストグラムを見る. なんとなくそれっぽく見えるが, どんどん分散が大きくなってしまう.

for(i in floor(exp(seq(log(10), log(N), length.out = 10)))){
  g <- d_rw %>% filter(t < i) %>% group_by(series) %>% summarise(ybar = sqrt(t) * mean(y), .groups = "drop") %>%
    ggplot(aes(x = ybar, y = stat(ndensity))) +
    geom_histogram(bins = 20, fill = "steelblue") + geom_vline(xintercept = 0, linetype = 2) +
    labs(x = expression(sqrt(N) * bar(y)[N]), subtitle = paste("N =", i)) +
    coord_cartesian(xlim = c(-230, 230)) + thm_hist
  print(g)
}

f:id:ill-identified:20210331205053g:plain — 図 8: ランダムウォーク時系列の $\sqrt{N}\bar{Y}_N$ のヒストグラム

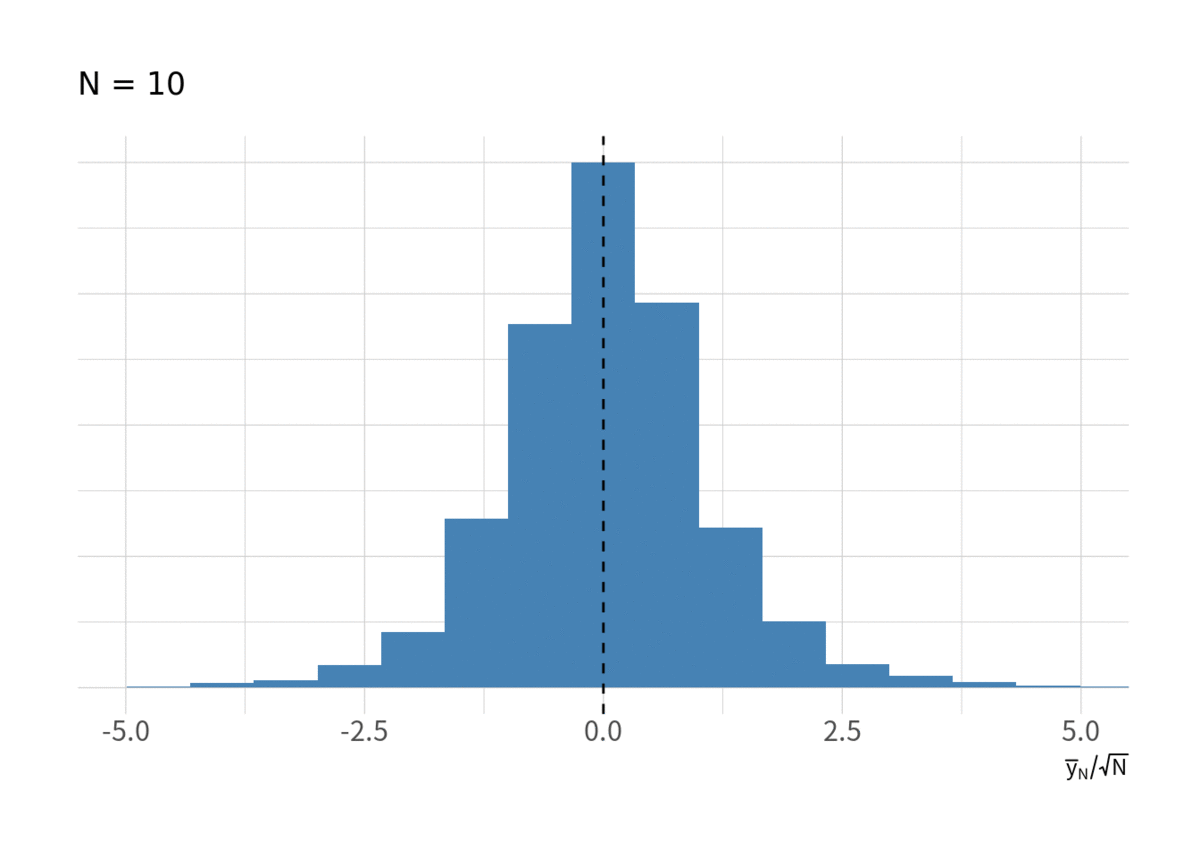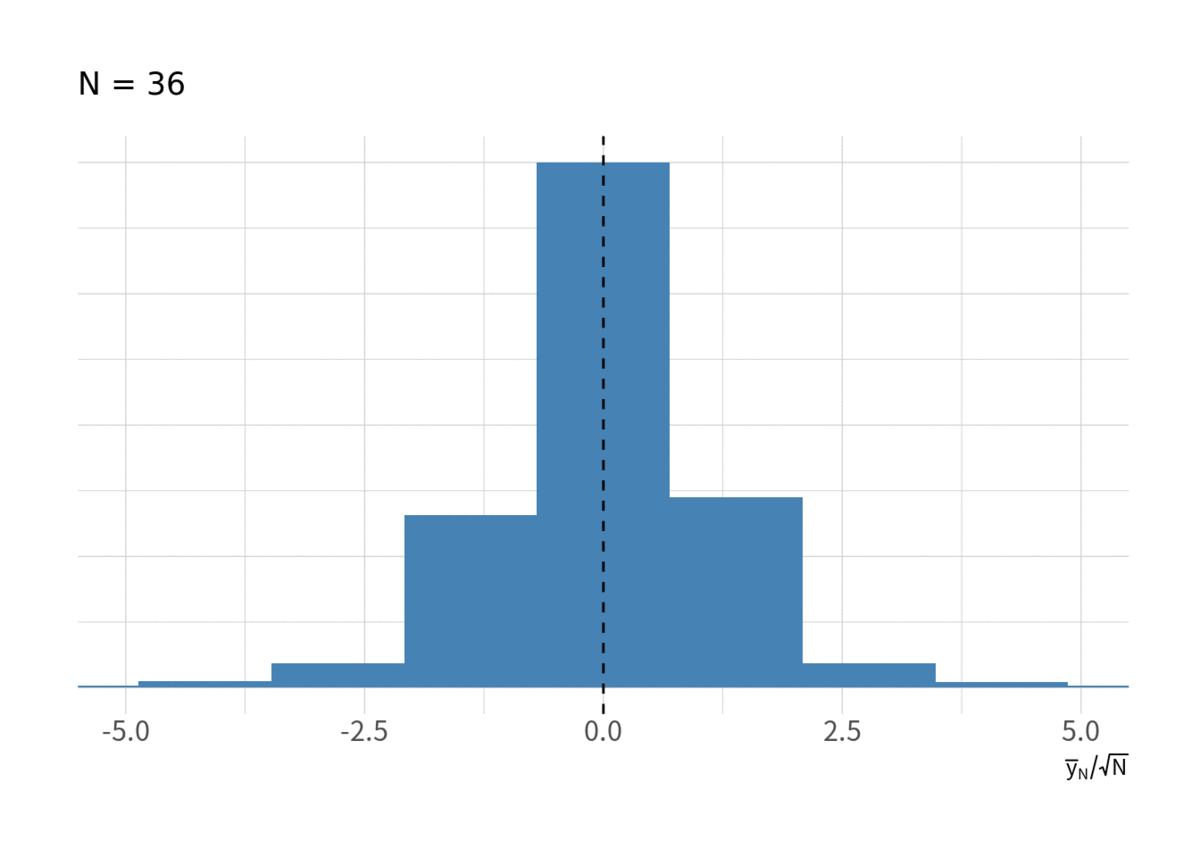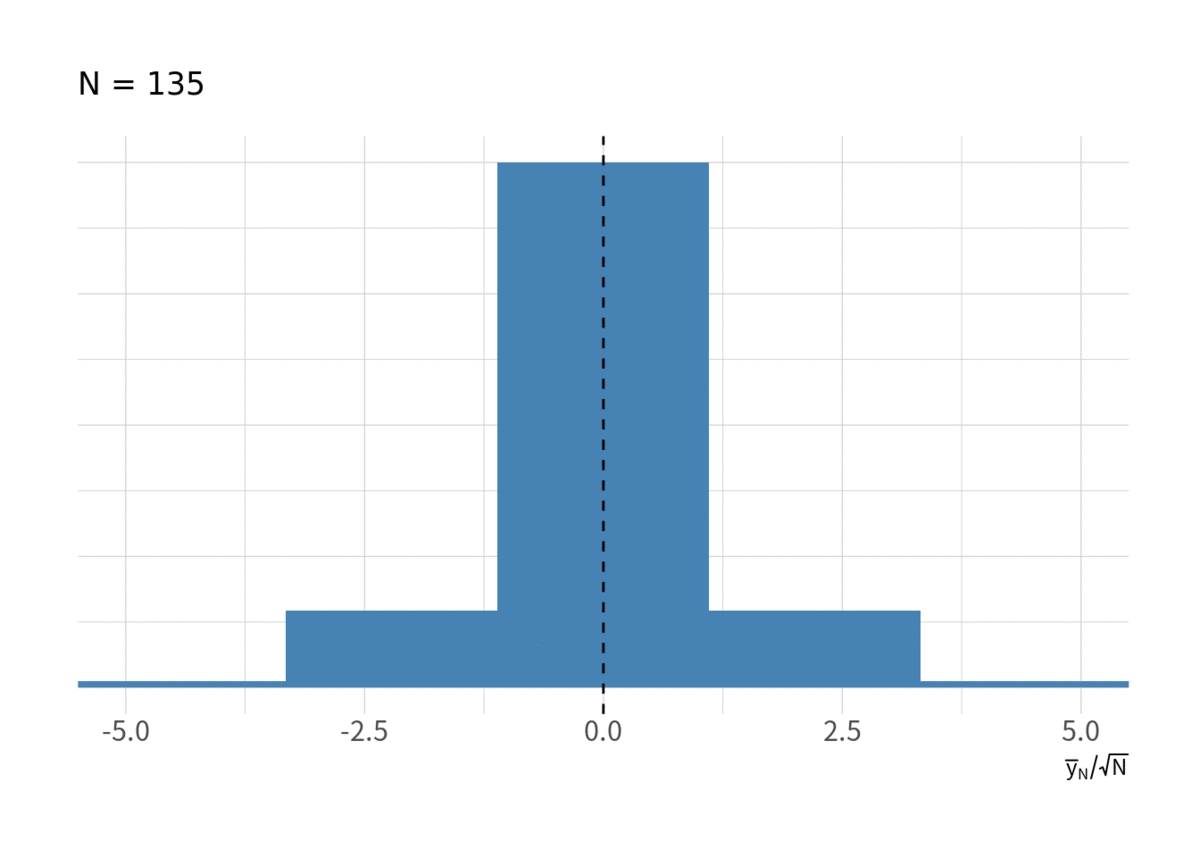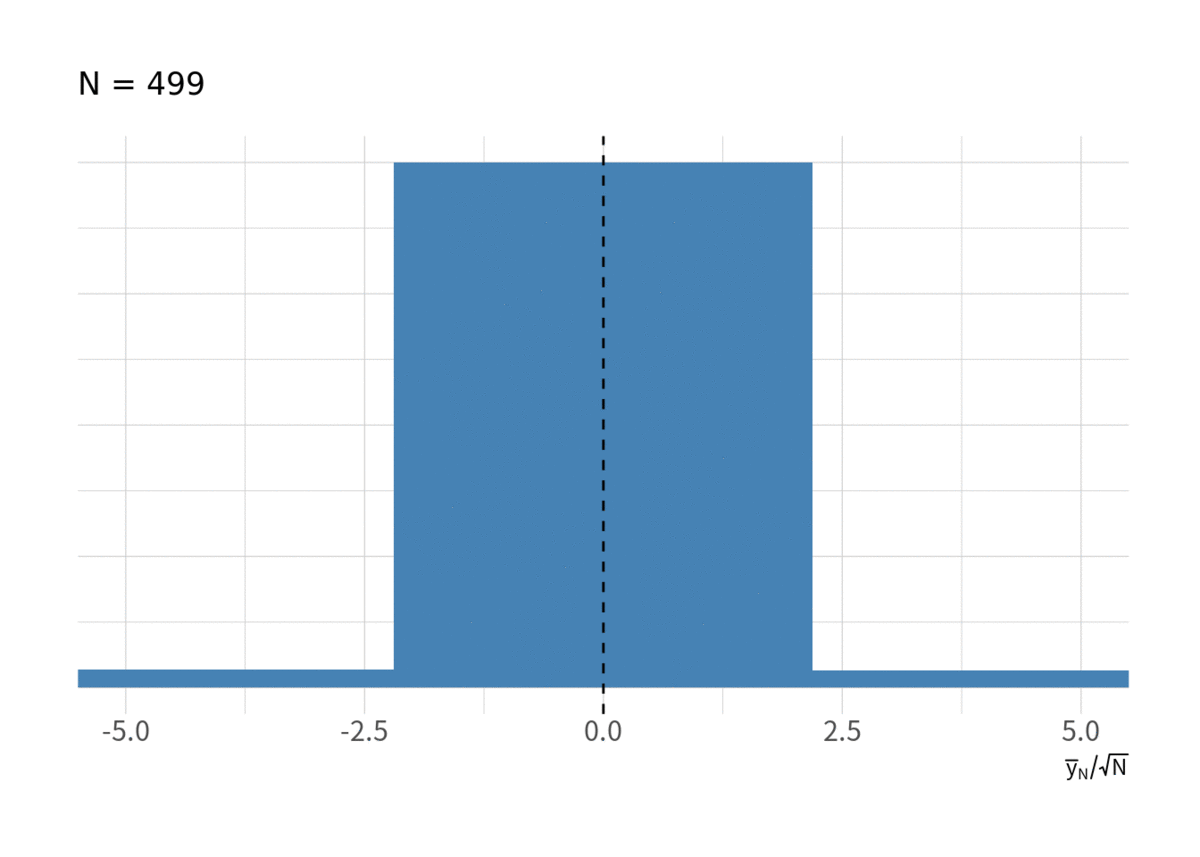
$N$ の増大に従って分散が大きくなっているのだから, 単純に $N$ で割って $\bar{Y}_N/\sqrt{N}$ としたらどうなるだろうか? それが図9である. しかし, やはり標準正規分布に近づいているようには見えない.

for(i in floor(exp(seq(log(10), log(N), length.out = 10)))){
  g <- d_rw %>% filter(t < i) %>% group_by(series) %>% summarise(ybar = mean(y)/sqrt(t), .groups = "drop") %>%
    ggplot(aes(x = ybar, y = stat(ndensity))) +
    geom_histogram(bins = 20, fill = "steelblue") + geom_vline(xintercept = 0, linetype = 2) +
    labs(x = expression(bar(y)[N] / sqrt(N)), subtitle = paste("N =", i)) +
    coord_cartesian(xlim = c(-5, 5)) + thm_hist
  print(g)
}

f:id:ill-identified:20210331205015g:plain — 図 9: ランダムウォーク時系列の $\bar{Y}_N/\sqrt{N}$ のヒストグラム

そして予想はつくと思うが, $\bar{Y}_N$ に関しても図10 のようにまったく収束していない.

d_rw %>% filter(series %in% sample(1:M, 7)) %>%
  group_by(series) %>% mutate(y_bar = cummean(y)) %>% ungroup %>%
  ggplot(aes(x = t, y = y_bar, group = factor(series), color = factor(series))) + geom_line() +
  geom_hline(yintercept = 0, linetype = 2) +
  labs(x = expression(N), y = expression(bar(y)[N])) +
  scale_color_pander()

f:id:ill-identified:20210331205154p:plain — 図 10: ランダムウォーク7系列の平均の収束

IID ではない AR(1) の時系列であっても正規分布に収束していたが, 同じく相関のあるランダムウォークの過程を見る, 今度は収束しているようには見えない. 実のところ, このランダムウォーク時系列 $\{Y_t\}$ に対して, $\bar{Y}_N/\sqrt{N}$ は $N\to\infty$ のとき標準ウィーナー過程 (別名, ブラウン運動) に収束する. これは Donsker の定理と呼ばれている*3.

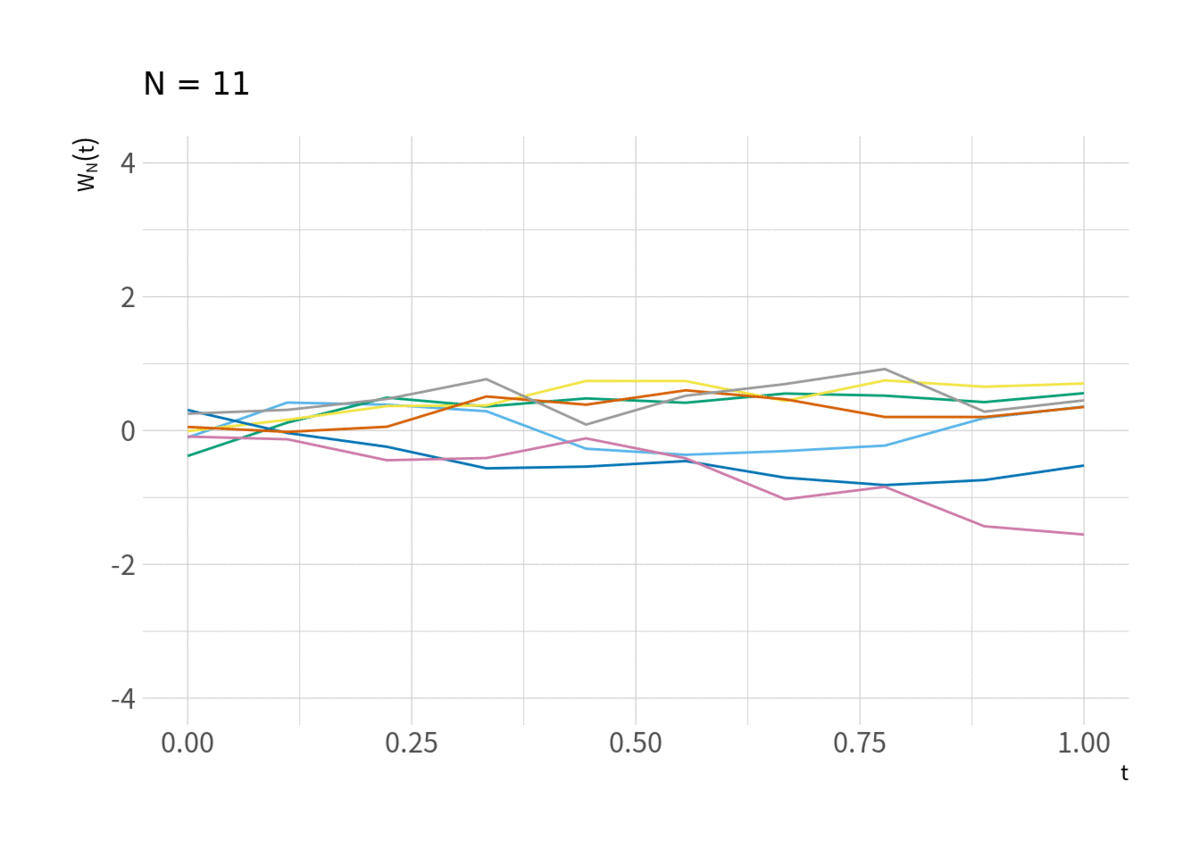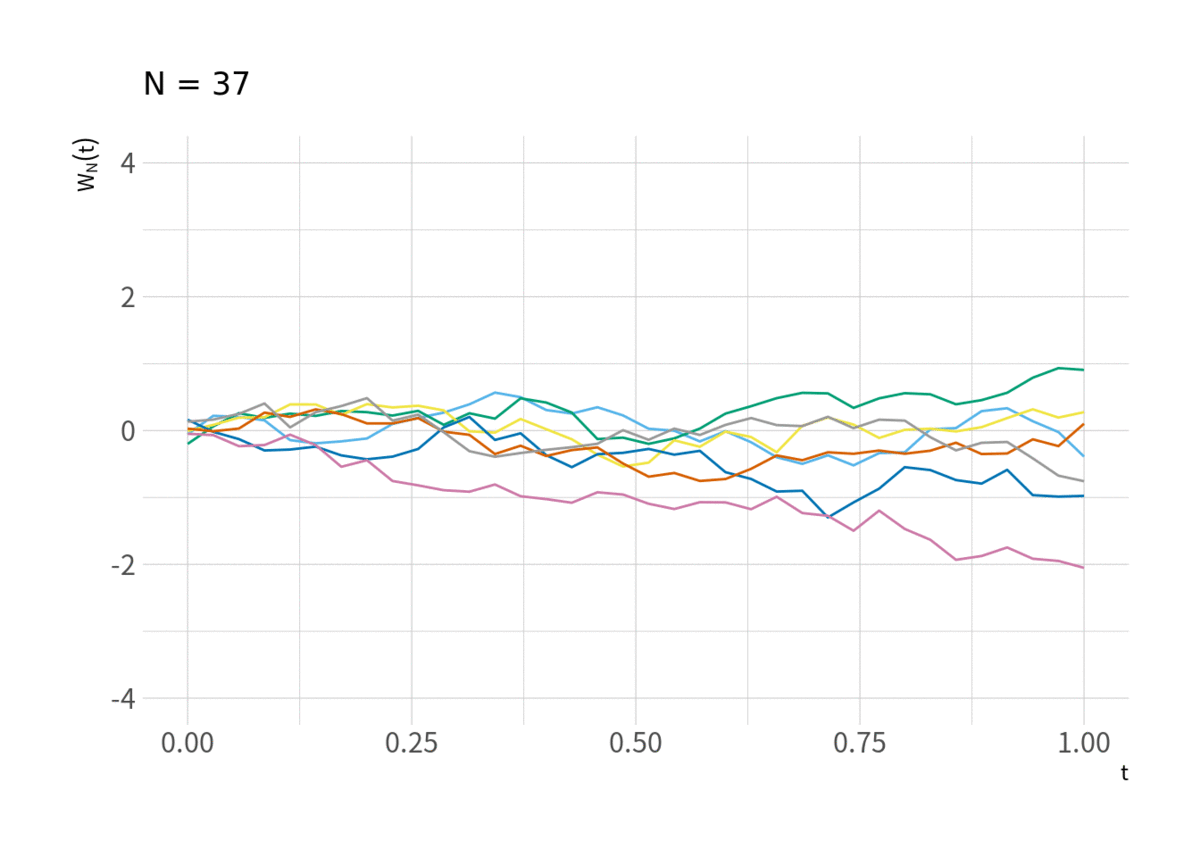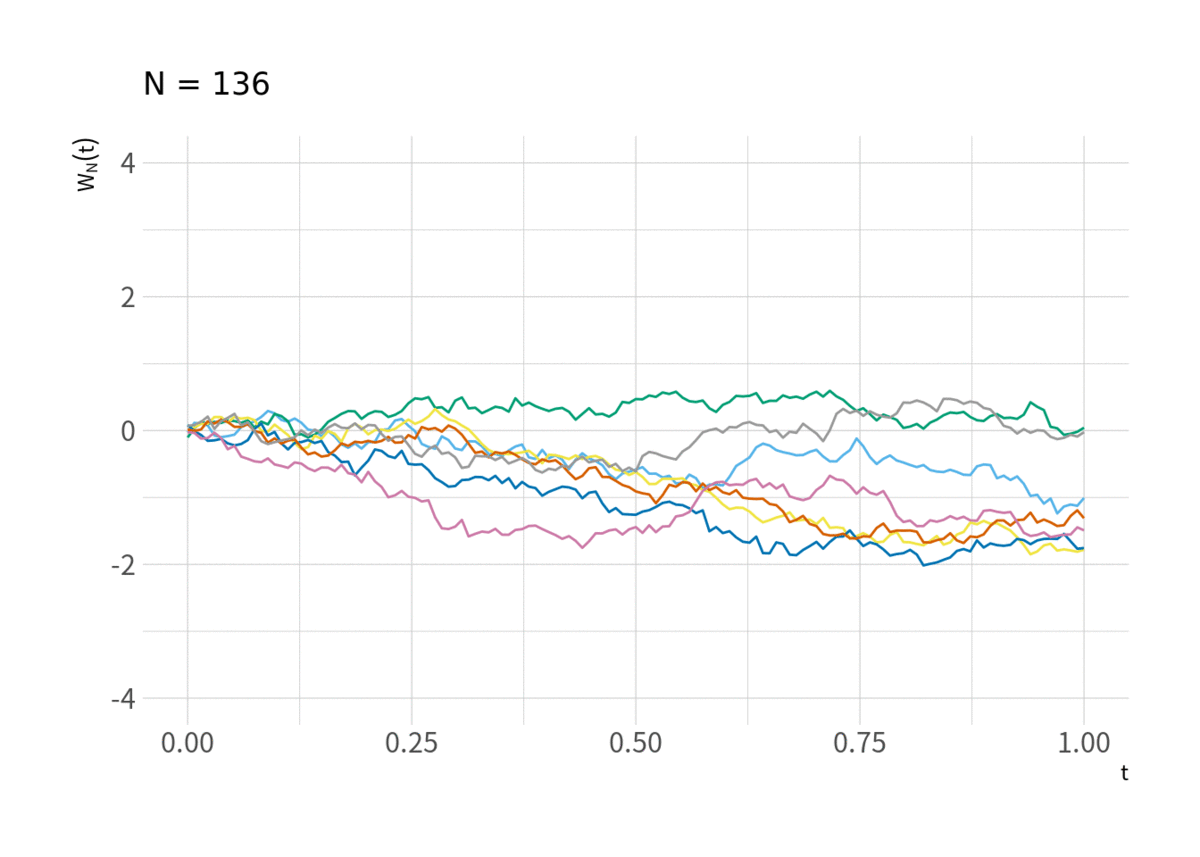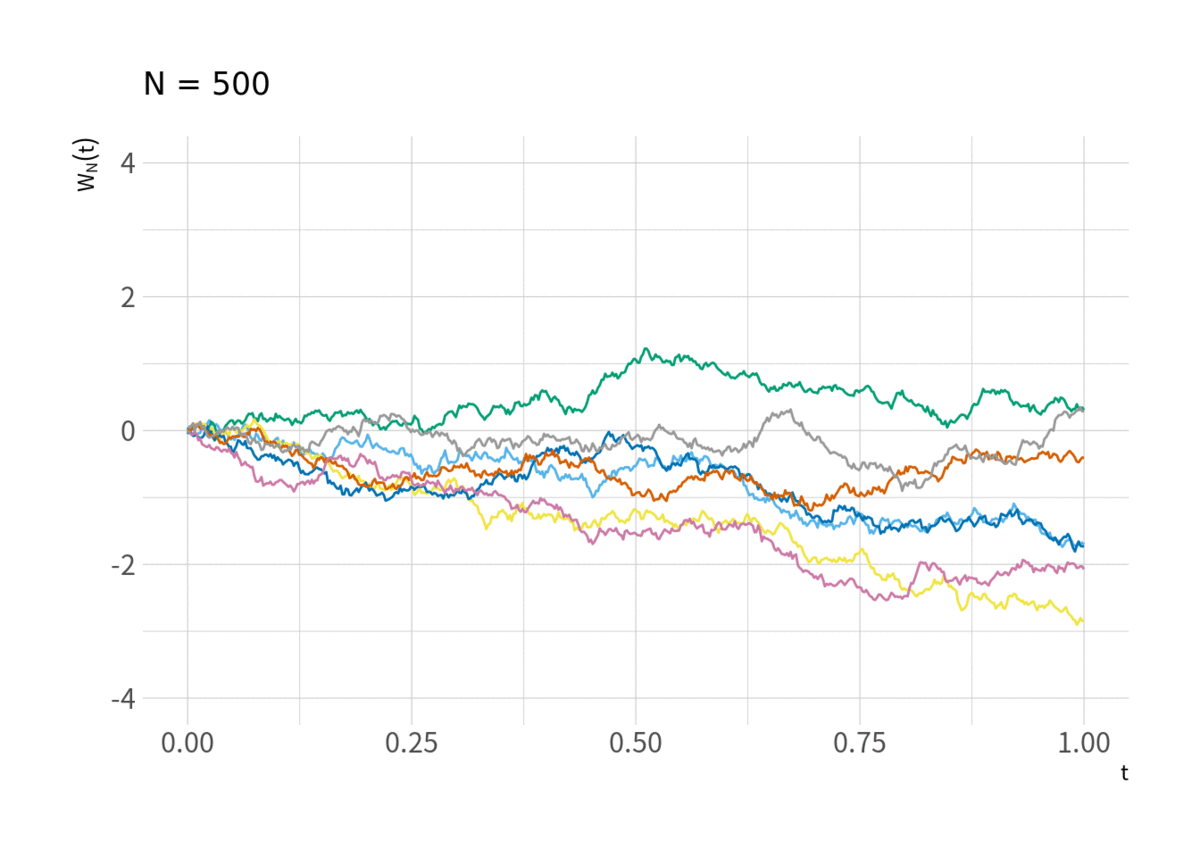
標準ウィーナー過程は $t\in[0,1$ ] 区間内の連続な確率過程である. つまり, これまでの $t = 0, 1, 2, \cdots$ のような離散的な点に対して確率を与えた数列ではなく, 連続区間に対して確率を与えたものである. Donsker の定理は, 大雑把に言えば, この連続な区間を2つ, 3つと区切って離散的に表現したものを, 区切りを無限に増やしていくと連続な確率過程に近似できるというものである. つまり, 期間の十分に多いランダムウォークの時系列 $Y_1,\cdots,Y_N$ に対して, $W_N(t) = Y_t/\sqrt{N}$ として, $N$ を増やしていくことで $W_N(t)$ がウィーナー過程に近づくのを見ることができる. それが図11 (と言ってもウィーナー過程を視覚的にイメージしづらいのでこれを見てウィーナー過程に近づいていることを納得するのは難しいかもしれない).

tmp <- d_rw %>% filter(series %in% sample(1:M, 7)) %>% mutate(t = t - 1)
for(i in floor(exp(seq(log(10), log(N), length.out = 10)))){
  g <- ggplot(filter(tmp, t < i),
              aes(x = t/max(t), y = y/sqrt(i), group = factor(series), color = factor(series))) +
    geom_line() + scale_color_pander() +
    labs(x = expression(t), y = expression(W[N](t)), subtitle = paste("N =", i + 1)) +
    scale_x_continuous(breaks = c(0, .25, .5, .75, 1)) + 
    coord_cartesian(xlim = c(0, 1), ylim = c(-4, 4))
  print(g)
}

f:id:ill-identified:20210331205238g:plain — 図 11: ウィーナー過程への近似

中心極限定理と比べ, ある1点を中心とした分布に収束するのではなく, ウィーナー過程という確率的な「経路」に収束するというのが Donsker の定理であり, 類似の定理も含め, 汎関数中心極限定理 (FCLT) または不変性原理 (Invariance Principle) と呼ばれている.

以上から, ランダムウォークの時系列に対しては標本平均 $\bar{Y}_N$ が収束せず, 大数の法則も中心極限定理も成り立たない. そのかわり, $N$ を大きくしていくと点ではなくその経路が標準ウィーナー過程に収束することになる.

なお, ウィーナー過程の性質として, $[0, 1$ ] 区間中の任意の $t\leq s$ に対して, $N\to\infty$ とするとそれぞれ独立に $W_N(s) - W_N(t) \sim\mathcal{N}(0, s - t)$ が成り立つので, $Y_t - Y_{t-1}$ に対しては従来の中心極限定理を当てはめることができる(図12). また, ウィーナー過程の終値 $W_N(1)/\sqrt{N}$ も中心極限定理の条件を満たしている (Beveridge–Nelson 分解).

d_rw %>% filter(series %in% sample(1:M, 7)) %>%
  group_by(series) %>% mutate(x = (y - first(y))/sqrt(n())) %>% 
  mutate(d = x - dplyr::lag(x, default = 0)) %>% 
  mutate(d_bar = cummean(d)) %>% ungroup %>%
  ggplot(aes(x = t, y = d_bar, group = factor(series), color = factor(series))) +
  geom_line() + geom_hline(yintercept = 0, linetype = 2) +
  labs(y = expression(bar(x)[t])) + scale_color_pander()

f:id:ill-identified:20210331210115p:plain — 図 12: ウィーナー過程の差分の収束

このように, ランダムウォークになるとこれまでのように正規分布に収束したりはしない, しかし一定の分布に収束するという数学の定理があるので, これをもとに検定や区間推定の式を導くことが出来る.

まだ疑わしいと感じる人はコードの冒頭の乱数のシード値を変えても収束するか確認したり, グラフに表示していない残り 993 系列を見たりすればいいだろう. 理論的な話が気になるならば数学的な解説のちゃんとした教科書を読んだりしてもいい. 数学的にもっと厳密な話を知りたいならば確率過程論の教科書なんかも読んだほうがいいと思うが, 統計学の応用では Donsker の定理単独であまり使われない気がする. よって数理統計学や金融工学の教科書など, 応用よりの教科書も読んだほうがいいかもしれない. 例えば Billingsley (2012) の Sec. 37 とか van der Vaart and Wellner (1996) の Sec.2.14 とか. 計量経済学の教科書なら, FCLT の厳密な証明は書かれていないが, 応用例が多く書かれている. 教科書は Hayashi (2000) Ch. 9 や Hansen (2021) の Ch. 16. 日本語の教科書が全く挙がってないが, 最近の教科書をあまり確認できていないためわからない. Hamilton の邦訳くらいか. あとは日本語で検索してもけっこう講義資料なんかが引っかかる.

金融工学/数理ファイナンスはあまり勉強してないので, 知っている範囲で言えば沖本 (2010) の5章.

統計学への応用

相関ありの中心極限定理の応用

すでにシミュレーションで見たように, 観測値どうしが独立でなく, 相関があっても中心極限定理が成り立つため, 一定の条件下では相関のある時系列データに自己回帰モデルを当てはめても問題なく, 係数の検定や区間推定も可能になる (詳細は Hayashi (2000) Ch. 6, Hansen (2021) Ch. 14 など).

汎関数 中心極限定理の応用

一方で, 上記の「一定の条件」を満たさないものを非定常時系列といい, その典型例が既に見せたランダムウォークである.

統計モデルでの典型的な応用例の1つは, 見せかけのトレンド問題である. 例えば今回のシミュレーションで生成したランダムウォーク系列を1つ取り出してみよう (図13).

d_rw %>% filter(series == 2) %>%
  ggplot(aes(x = t, y = y)) + geom_line() + geom_smooth(method = "lm", formula = y ~ x)

f:id:ill-identified:20210331205339p:plain — 図 13: ランダムウォークと見せかけのトレンド

このように一見すると直線的な上昇トレンドがある時系列に見えなくもない. しかしランダムウォークの性質から, このグラフで見えてないt=501以降の期間では下降トレンドになる (ランダムウォークのこのような挙動は確率的なトレンドなので, 下降トレンドというと確定的なニュアンスがありあまり適切な表現ではないが) 可能性が十分にある. そこで, $Y_t = \alpha + \delta t$ のような時間変数で表現できる, 線形トレンドのモデルであると, わざと誤って回帰してみよう.

tidy(lm(y ~ t, data = d_rw %>% filter(series == 2)))

term	estimate	std.error	statistic	p.value
(Intercept)	1.232	0.3833	3.215	0.001389
t	0.04047	0.001326	30.53	3.899e-116

$\alpha$ も時間変数 $t$ の係数 $\delta$ も有意であるという結果になった. これは冒頭で紹介したような中心極限定理が成り立たず, 分布が正規分布に収束しないため通常のt検定が意味をなさなくなるためである(厳密に言えば, 個別の事例に関してはこのような誤った検定結果が第1種/第2種の過誤なのか見せかけのトレンドなのかを識別することは難しいが, 理論上問題が発生する). そしてもちろん, ランダムウォークを誤って上昇トレンドとみなしてしてしまったモデルは予測にも使えない.

では非定常な時系列では仮説検定ができないのかというと, そうでもない. FCLTのもう1つの応用例は, ランダムウォークのような非定常過程であるかどうかを検定する, (以前の投稿でも言及した) Dickey-Fuller 検定というものもある (図14). これも詳しい話は計量経済学のちゃんとした教科書でなされているのでそちらを参照してほしい.

f:id:ill-identified:20210331210321p:plain — Dickey-Fuller 分布と正規分布, 以前の投稿の使い回し

参考文献

Billingsley, Patrick. 2012. Probability and Measure. Anniversary ed. Wiley Series in Probability and Statistics. Hoboken, N.J: Wiley.

Probability and Measure (Wiley Series in Probability and Statistics)

作者:Billingsley, Patrick
Wiley

Amazon

Hansen, Bruce. 2021. “Econometrics.” here.

Hayashi, Fumio. 2000. Econometrics. Princeton: Princeton University Press.

Econometrics

作者:Hayashi, Fumio
Princeton University Press

Amazon

van der Vaart, Aad W., and Jon A. Wellner. 1996. Weak Convergence and Empirical Processes. With Applications to Statistics. Springer Series in Statistics. New York, NY: Springer New York. DOI: 10.1007/978-1-4757-2545-2.