[python] [stan] 潜在変数と階層ベイズ法と RFM 分析 [未完成]

概要
モデル
プログラム
用いるデータ
結果
まとめ (暫定)
参考文献

概要

2017/2/26 追記: 続編で適切なプログラムを書きました。この記事の「プログラム」のセクションは無視してください。
ill-identified.hatenablog.com

小売業の分析に RFM 分析というものが使われる. ここでは阿部 (2011) で提案された, RFM 分析と階層ベイズ法を組み合わせた新しい方法を python 3.4 と stan 2.9 で実装し, 実際の購買データを使って推定してみた.
そろそろ RFM 分析について何か書こうかと思った矢先,
abrahamcow.hatenablog.com
という記事を書かれてしまったが (こちらは RF 分析だが, RFM と本質的にあまり違いがない.), MCMC を使う方法は使われてなかったので続きを横取りしてみた*1.
python を使ったのは個人的な練習のため. サイズの大きなデータを扱うようになると, どうしてもインメモリで処理する R だけでは不便になってくる. メモリ増設とか Amazon EC2 を使うとか、そのへんの敷居は昔よりたしかに低くなってきてるが貧乏性というか貧乏なので python に手を出すことにしている.
今回は文章だけで6ページぶんくらいあるので長い.
~~まだ完全ではない~~ -> 解決した

RFM 分析というのは, 小売業が Recency (どれだけ最近に買ったか), Frequency (どれくらいの頻度で買ったか), Monetary (いくら買ったか) という3次元の切り口で顧客ごとにどれくらい売り上げに寄与しているかを分析する手法である. 単純にわかりやすいだけでなく, RFM の指標があれば顧客生涯価値 (CLV) の推測ができたり, 顧客の年齢性別などの属性と紐付けられればどういう層が最も売り上げに寄与しているかがわかり, 次の施策を考えることができる.

阿部 (2004) では, RF 分析が購買を続ける期間の長さという情報を捨てていることを指摘している. Recency が良くてもそれが最後の購買で, 以後購入することがないかもしれないし, Frequency が悪くても継続的に購入してくれるリピート客がいるかもしれない. そもそも, R は本来は直接観測できない「離脱」を推測すると経験的に考えられてきた指標である. そこで, これらの研究は間接的に生存期間をはかるように顧客の生存期間がある分布にしたがうと仮定したモデルを提案している:

観測期間*2 $T$ の間で, 最初の購買から最後の購買までの期間 $t$ とおくと, $T-t$ は Recency に対応することになる. しかし, これだけでは観測終了後も購買を持続するのか, $t$ から $T$ まで, つまり Recency の期間中に離脱し, それ以降は購買しないのかは分からない ((阿部 2008) の図3参照). これを解決する方法を提案したのが上の論文である.

モデル

ここでは, 阿部 (2008), Abe (2009), 阿部 (2011) で提案されたモデルの解説をする. Abe (2009) は阿部 (2008) を英語化しただけなので, 結局全て日本語で読めてしまうが, 式展開の説明が簡素すぎたり誤植があったりするので, ここで再度解説する.

阿部 (2008), Abe (2009) では, モデルを階層ベイズ法を用いて推定する*3バージョンを提案していた. 顧客個人の異質性を, 顧客の期待生存期間 ( $\mu$ ) と期待購買頻度 ( $\lambda$ ) の 2つの平均パラメータを 2変量対数正規分布にしたがう異なるパラメータとして表現し, この対数正規分布の平均パラメータを顧客の年齢や性別などの属性を説明変数とした回帰モデルとしていた:

$\begin{align} \begin{bmatrix}\ln\lambda_{i}\\ \ln\mu_{i} \end{bmatrix}\sim & \mathcal{N}(\boldsymbol{\theta}_{i}=\mathbf{X}_{i}\boldsymbol{\beta},\,\boldsymbol{\Gamma}_{0})\label{eq:RF-prior}\end{align}$

さらに, 阿部 (2011) では, これまでの研究で明示的に取り入れていなかった Monetary の要素を取り入れて RFM 分析への拡張として再定式化したモデルを使用した:

$\begin{align} \begin{bmatrix}\ln\lambda_{i}\\ \ln\mu_{i}\\ \ln\eta_{i} \end{bmatrix}\sim & \mathcal{N}\left(\boldsymbol{\theta}_{i}=\mathbf{X}_{i}\boldsymbol{\beta},\,\boldsymbol{\Gamma}_{0}\right)\label{eq:RFM-prior}\end{align}$

さらに, 生存期間は指数分布に, 購買回数はポアソン分布に, 購買金額は対数正規分布にしたがうと仮定する.

$\begin{align} p(\tau_{i}|\mu_{i})= & \mu_{i}\mathrm{e}^{-\mu_{i}\tau_{i}},\tag{生存期間}\label{eq:survaival}\\ p(x_{i}|\lambda_{i})= & \begin{cases} \frac{(\lambda_{i}T_{i})^{x_{i}}}{x_{i}!}\mathrm{e}^{-\lambda_{i}T_{i}} & \text{if }\tau_{i}>T_{i}\\ \frac{(\lambda_{i}\tau_{i})^{x_{i}}}{x_{i}!}\mathrm{e}^{-\lambda_{i}\tau_{i}} & \text{if }\tau_{i}\leq T_{i} \end{cases},\tag{購買回数}\label{purchase}\\ \ln s_{i}\sim & \mathcal{N}(\ln\eta_{i},\,\omega_{i}^{2})\tag{購買金額}\label{eq:money}\end{align}$

と仮定している. 阿部 (2011) はこの仮定を置いた理由として, (1) 購買金額は正であること, (2) 個人ごとの購買金額の分布をヒストグラムで確認すると, 左右非対称な対数正規分布と似ていること, という2点を挙げている*4.

さらに個人の異質性を表現するため, $\mu$ , $\lambda$ , $\eta$ の各パラメータを顧客のデモグラフィック属性で回帰することができるが, 本稿ではデモグラフィック属性がないので行わない.

次に, 尤度がどのようになるかを考える. 潜在変数は実際には $T$ 期間を超えて生存しているかどうかという $\zeta:=1(\tau>T)$ と, その期間を表す $\tau$ の2つが存在することになる. まず, 期間 $T$ 以降も生存している確率は, パラメータ $\mu$ を用いて相補分布から $\bar{F}_{\mathit{exp}}(T|\mu)=1-F_{\mathit{exp}}(T|\mu)=\exp(-T\mu)$ と表せる. ただし, $\bar{F}_{\mathit{exp}}$ は指数分布の相補分布関数である. さらに, $t$ までに $x$ 回の購買が発生する確率はパラメータ $\lambda$ , $x$ のガンマ分布で表せる*5 *6: $x$ 回目の購買が発生するまでの期間 $t$ を連続分布として表現すると, その分布関数は

$\begin{align} F(t)= & 1-\mathrm{P}\{X\leq x-1\}\end{align}$

となる. 購買イベントはそれぞれ独立に発生するから,

$\begin{align} F(t)= & 1-\sum_{k=0}^{x-1}\frac{(\lambda t)^{k}}{k!}\mathrm{e}^{-\lambda t}\\ = & 1-\mathrm{e}^{-\lambda t}\sum_{k=0}^{x-1}\frac{(\lambda t)^{k}}{k!}\end{align}$

となる. 分布関数を微分すれば密度関数になるので,

$\begin{align} f(t)= & \lambda\mathrm{e}^{-\lambda t}\sum_{k=0}^{x-1}\frac{(\lambda t)^{k}}{k!}-\mathrm{e}^{-\lambda t}\sum_{k=0}^{x-1}\frac{\lambda k(\lambda t)^{k-1}}{k!}\\ = & \lambda\mathrm{e}^{-\lambda t}\left[\sum_{k=0}^{x-1}\frac{(\lambda t)^{k}}{k!}-\sum_{k=1}^{x-1}\frac{(\lambda t)^{k-1}}{(k-1)!}\right]\\ = & \lambda\mathrm{e}^{-\lambda t}\left[\sum_{k=0}^{x-1}\frac{(\lambda t)^{k}}{k!}-\sum_{k=0}^{x-2}\frac{(\lambda t)^{k}}{k!}\right]\end{align}$

となる. ここで,

$\begin{align} \left[1-1\right]+\left[\frac{\lambda t}{1!}-\frac{\lambda t}{1!}\right]+\left[\frac{(\lambda t)^{2}}{2!}-\frac{(\lambda t)^{2}}{2!}\right]+\cdots+\frac{(\lambda t)^{x-1}}{(x-1)!}= & \frac{(\lambda t)^{x-1}}{(x-1)!}\end{align}$

となるから,

$\begin{align} f(t)= & \lambda\mathrm{e}^{-\lambda t}\frac{(\lambda t)^{x-1}}{(x-1)!}\\ = & \frac{\lambda^{x}t^{x-1}}{(x-1)!}\mathrm{e}^{-\lambda t}\end{align}$

$x$ が整数なので, $\Gamma(x)=(x-1)!$ となり, ガンマ分布になることがわかる.

次に, 仮定より過去にたいして独立に購買が発生するから, $[t,\,T$ ] で購買の発生しない確率はポアソン分布で表せるので, $T$ 以降も生存するもとで, 観測された購買歴の発生する確率は,

$\begin{align} p\{\tau>T|x,\,t,\,T\}= & f_{\Gamma}(t|\lambda,\,x)\cdot f_{\mathit{po}}(0|\lambda R)\\ = & \frac{\lambda^{x}t^{x-1}}{\Gamma(x)}\mathrm{e}^{-\lambda t}\frac{(\lambda(T-t))^{0}}{0!}\mathrm{e}^{-\lambda(T-t)}\\ = & \frac{\lambda^{x}t^{x-1}}{\Gamma(x)}\mathrm{e}^{-\lambda T}\end{align}$

ただし, $f_{\Gamma}$ はガンマ分布の密度関数である. 一方で, $[t,\,T$ ] までに離脱している場合は, $t$ までに $x$ 回購買がなされ, かつ $[t,\,\tau$ ] までに購買が発生しない, かつ, $[t,\,T$ ] の間に離脱している確率になる. $\tau$ で周辺化すれば,

$\begin{align} p\{\tau\in[t,\,T]|\lambda,\,t,\,T,\,\mu\}= & \int_{t}^{T}f_{\Gamma}(t|\lambda,\,x)\cdot\mathit{Po}(0|\lambda(\tau-t))\cdot\bar{F}_{\mathit{exp}}(\tau|\mu)d\tau\\ = & \frac{\lambda^{x}t^{x-1}}{\Gamma(x)}\mu\int_{t}^{T}\mathrm{e}^{-(\lambda+\mu)\tau}d\tau\\ = & \frac{\lambda^{x}t^{x-1}}{\Gamma(x)}\frac{\mu}{\lambda+\mu}\left[\mathrm{e}^{-(\lambda+\mu)T}-\mathrm{e}^{-(\lambda+\mu)t}\right]\end{align}$

以上から, ベイズの定理で $T$ 以降も生存している確率を,

$\begin{align} p(\tau>T|\lambda,\mu,\,x,\,t,\,T)= & \dfrac{f_{\Gamma}(t|\lambda,\,x)f_{\mathit{po}}(0|\lambda R)\bar{F}_{\mathit{exp}}(T|\mu)}{f_{\Gamma}(t|\lambda,\,x)f_{\mathit{po}}(0|\lambda R)\bar{F}_{\mathit{exp}}(T|\mu)+p\{\tau\in[t,\,T]|\cdots\}}\nonumber \\ = & \dfrac{\mathrm{e}^{-(\lambda+\mu)T}}{\mathrm{e}^{-(\lambda+\mu)T}+\frac{\mu}{\lambda+\mu}\int_{t}^{T}\mathrm{e}^{-(\lambda+\mu)\tau}d\tau}\nonumber \\ = & \dfrac{1}{1+\frac{\mu}{\lambda+\mu}\left\{ \exp\left[(\lambda+\mu)R\right]-1\right\} }=p(\zeta=1|\cdots)\label{eq:zeta-prob}\tag{1}\end{align}$

と表せる. 生存期間が $\tau>T$ , つまり $T$ 後も生存しているかどうかを表すインジケータを $\zeta$ とする*7. $\zeta=1$ のとき, 尤度は

$\begin{align} \mathcal{L}(\boldsymbol{\theta}|\zeta=1,\,\mathcal{D})= & f_{\Gamma}(t|x,\,t)\bar{F}_{\mathit{Exp}}(T|\mu)f_{\mathit{po}}(0|\,\lambda(T-t))\\ = & \frac{\lambda^{x}t^{x-1}}{\Gamma(x)}\mathrm{e}^{-(\lambda+\mu)T}\end{align}$

であり, $\zeta=0$ のとき,

$\begin{align} \mathcal{L}(\boldsymbol{\theta},\tau|\zeta=0,\,\mathcal{D})= & f_{\Gamma}(t|x,\,t)f_{\mathit{po}}(0|\lambda(\tau-t))f_{\mathit{Exp}}(\tau|\mu)\\ = & \frac{\lambda^{x}t^{x-1}}{\Gamma(x)}\mu\mathrm{e}^{-(\lambda+\mu)\tau}\end{align}$

となる. $\zeta$ を用いて集約して表すと, 対数尤度は

$\begin{align} \mathcal{L}= & \dfrac{\lambda^{x}t^{x-1}}{\Gamma(x)}\mu^{1-\zeta}\mathrm{e}^{-(\lambda+\mu)\left\{ \zeta T+(1-\zeta)\tau\right\} }\\ \ln\mathcal{L}= & x\ln\lambda+(x-1)\ln t-\ln\Gamma(x)+(1-\zeta)\ln\mu\\ & -(\lambda+\mu)\left[\zeta T+(1-\zeta)\tau\right]\end{align}$

となる. 購買金額の尤度は, これらと複雑に結びついてはいないので, 単に上記の対数尤度に正規分布の対数尤度を足すだけでよい.

さらに, ここでは見やすさのため省略したが, 実際には個人を表すインジケータが付いており, 顧客の数だけこれを繰り返し足すことになる.

また, 実際にはリピートがない場合もあり, $x=0$ になることがある. $\Gamma(0)$ は定義できないが, リピートがない場合は同時に $t=0$ でもあるはずなので, この場合の尤度はガンマ関数が分母になっている分数部分が消えた
$\begin{align} \mathcal{L}(\boldsymbol{\theta},\tau|\zeta=0,\,\mathcal{D})= & \mu^{1-\zeta}\mathrm{e}^{-(\lambda+\mu)\left\{ \zeta T+(1-\zeta)\tau\right\} }\end{align}$
になる。

プログラム

2017/2/26 追記: 以下の解決編で適切なプログラムに更新しました。このセクションは無視してください。
ill-identified.hatenablog.com

以下は stan で実装するにあたっての技術的な解説.

このモデルは, 複雑な尤度となるため, 通常の方法では計算が難しい. 元論文では階層ベイズ法と称しているが, むしろ潜在変数 $\zeta$ , $\tau$ が重要で, 紹介されている計算手順もモンテカルロ EM アルゴリズムに近いものだった. しかし提案されているのと全く同じ計算手順を実装するのでは芸がないし, 流用可能性を高めることも考えて今回も stan を使って計算してみる.

3つのパラメータの事前分布は, 阿部 (2011) 同様, 対数多変量正規分布にしたがうとする. 今回は購買歴に紐付けられる顧客のデモグラフィック属性データがないため, パラメータは全ての顧客で同じと仮定し ( $\boldsymbol{\theta}_{i}=\boldsymbol{\theta}_{0}$ ) 適当な事前分布を設定する. ハイパーパラメータ $\boldsymbol{\Gamma}_{0}$ の事前分布は, 逆ウィッシャート分布

$\begin{align} \boldsymbol{\Gamma}_{0}\sim & \mathit{IW}(\boldsymbol{v}_{00},\boldsymbol{\Gamma}_{00})\label{eq:prior-wishart}\end{align}$

を利用する. $\boldsymbol{\theta}_{i}$ には要素ごとに独立な一様分布を, $v_{00}$ , $\boldsymbol{\Gamma}_{0}$ には適当な定数を与えた.

パラメータ推定だけでは実用上あまり意味がないので, 阿部 (2011) で書かれているように顧客生涯価値の計算*8を generated quantities ブロックで計算する. なお, 計算上は $\lambda$ , $\mu$ , $\eta$ は1つのベクトルで表すとやりやすいが, それだと結果を取り出す際にめんどくさいので, model ブロックではベクトルとして扱い, generated quantities ブロックで個別の名前の変数に代入することにした. 対数スケールから戻す処理もその際に行なっている.

なお, $s$ は他の分布とはあまり複雑に関係していない. 事実, 阿部 (2008), Abe (2009) は M 要素の推定を除いた以外は阿部 (2011) とほとんど同じである. 購買歴がなく平均額の情報しかない場合などは分布を推定できないので, 顧客生涯価値の計算にそのまま平均値を利用するという妥協策もある. 今回は他2要素とまとめて推定するようなプログラムにした.

Stan を使う場合の技術的なハードルは, ゼロまたは 1 をとる離散パラメータ (潜在変数) である $\zeta$ の扱い方である. Abe (2009), 阿部 (2011) に書いてある手順そのままに $\zeta$ のベルヌーイ乱数を発生させ, 条件分岐で尤度を計算する……, としたいところだが, stan は離散パラメータを利用できないので, ver. 2.9 リファレンスの 12章に書いてあるように, EM アルゴリズムのように潜在変数を周辺化することで除去するという方法もあるが, $[0,\,1$ ] の一様乱数を一旦生成し, $(\ref{eq:zeta-prob})$ の確率と比較して $\zeta$ を決定することにした.

尤度は組み込み関数を組み合わせても記述できるが, そもそも事前分布では $\lambda$ , $\mu$ , $\eta$ は対数で与えられていること, 尤度がすでに導かれていることなどから, 精度向上のため increment_log_prob() を使って対数尤度を直接記述する. また, $T$ , $t$ はデータでは日数だが, 指数変換した際の桁溢れ*9対策のため, 365で割ることにした*10.

gist74e6adddc2810a7d3333a348b2d390ea

用いるデータ

UCI Machine Learning Repository UCI Machine Learning Repository: Online Retail Data Set の Online Retail のデータを利用して計算する. もともとは Chen, Sain, and Guo (2012) で使用されたもので, 英国のオンライン通販サービスの購買履歴である. 購入者の大半は英国在住. この企業は 1981年からカタログや電話注文など古典的な販売業態を通してきたが, 2年前 (当時) から web 通販サイトを立ち上げた, という状態らしい. データは 2010年12月から2011年12月まである*11.

顧客生涯価値の計算には割引率を与える必要があるが, ここでは参考文献と同じ年 15 %, 日単位で約 2.7 %を採用した. オンライン販売のログでやっかいなのは, 注文数量がマイナスのレコードが存在するということである. おそらく返品を表すので, これをうまく処理しなければならない*12. さらに今回のデータでは, 返品の記録がどの注文に対応するかが分からない*13. そこで, 返品を売り上げに参入しないで, 可能な限りそれらしい購買歴を再現することになる. 具体的には, まず, 顧客ID や商品ID, 日付の欠けているようなレコードは不適正なものとしてトランザクションデータから除く. 次に顧客ID, 商品ID, ごとに日付と注文/返品の区分でソートする. 日付を直前の注文レコード日付に修正し, 顧客ID, 商品ID, 日付で売上額を集計して (返品の額はマイナスである) これを実際の売上額と仮定する. 必ずしも注文レコードと対応する返品レコードが連続して現れるという保証はないが, 完全に再現できないのでどこかで妥協する必要がある. 額がゼロ以下になった場合はその注文は購買の発生とみなさず除外する. さらに, 実際に計算したところ, 1ポンド未満のレコードが多く発生したため, 1ポンド以上のレコードのみを使うことにした. この方法で補正した購買歴をもとに, RFM 指標を計算し, 各パラメータを推定する.

また, 全ての購買記録を推定に用いることは出来ない. 観察期間ギリギリの記録では, $T$ がほとんどゼロとなり, $(\ref{purchase})$ 式のポアソン分布のパラメータがゼロになってしまい推定できない. よって, ある程度の観察期間を確保した顧客しか推定に使うことができない. そこで, 2010/12 中に最初の購買が観測された顧客約800人のデータだけを利用する.

以下がそのデータの記述統計.

以下がデータ読み込みから stan 呼び出しまでのプログラムで, python 3.4 で pandas などを使い, 最後に pystan で stan を呼び出している (jupyter notebook で起動) のだが, stan の実行中にクラッシュしてしまったので急いで R でやり直すことに*14……

なお, パラメータが多いので, 結果だけでも数 GiBになるし実行にもそれなりに時間がかかるのでラップトップなんかではやらないほうがいい (AWS などを使うのが手頃か).

以下は pandas などを使って元のエクセルファイルを加工する際に使ったプログラム (jupyter notebook 製)

gist48183856a4f702495d09627e80762f76

こちらは stan を呼び出して結果を集計する部分のみの R プログラム

gistf3505d462c218889bfc2dc739c3cb4d5

結果

実際に 4系列ぶんを HMC で計算したところ, 10000回以上試行しても収束ができてない. $\boldsymbol{\theta}_{0}$ の traceplot の結果が以下のような感じになっている.

f:id:ill-identified:20160501145426p:plain

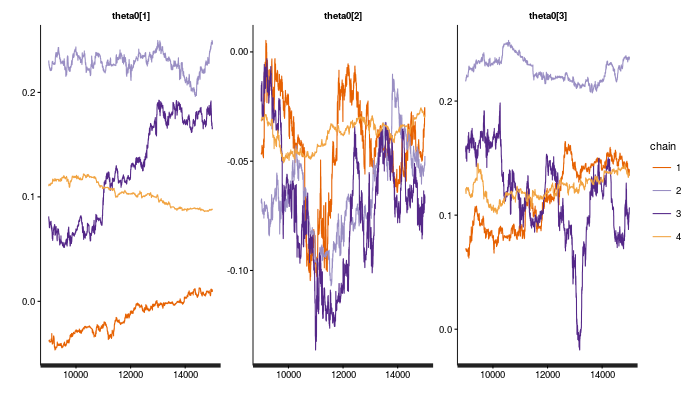
さらに, $\tau$ を生成する部分で $[t,\,T$ ] 区間の切断分布がうまく計算できずにエラー終了になる*15. とりあえず上限だけ設定した分布を使用し, 初期値も $t,\,T$ の平均値とした. 制約が上限だけのため, 結果を見るとところどころ制約に反した推定値がある.

       ID      lambda        mu        eta          CLV        zeta       tau        time      Time     Recency Freq   Monetary tau_well
1   12347   1.3078056 0.4086655  1.2870040 8.158768e+01 1.000000000 0.9733374 1.000000000 1.0054795 0.005479452    6  615.71429    FALSE
2   12348   1.6625851 2.4840424  1.7288114 4.379591e+01 0.750000000 0.8565919 0.775342466 0.9808219 0.205479452    3  449.31000     TRUE
3   12370   1.7328658 0.8952195  3.8260184 1.112647e+02 1.000000000 0.9513447 0.846575342 0.9863014 0.139726027    3  886.42250     TRUE
4   12377   1.1134659 2.2886246  2.9850735 1.393666e+01 0.250000000 0.5148699 0.106849315 0.9698630 0.863013699    1  814.06000     TRUE
5   12383   2.0070310 0.9343815  1.8970712 4.049933e+01 0.750000000 0.7059199 0.460273973 0.9643836 0.504109589    4  370.11200     TRUE
6   12386   3.8162737 2.4334077  0.8428730 3.698143e+01 0.250000000 0.5607973 0.079452055 1.0027397 0.923287671    1  200.95000     TRUE
7   12395   2.8444934 0.5785159  2.3825207 1.029625e+02 1.000000000 1.0755528 0.964383562 1.0164384 0.052054795   10  274.42091     TRUE
8   12417   4.4139054 2.4496696  5.9556794 1.401208e+02 1.000000000 0.9946779 0.969863014 0.9780822 0.008219178    8  405.45556     TRUE
9   12423   2.5468153 0.3421147  2.5822287 8.832888e+01 1.000000000 0.9258729 0.967123288 0.9671233 0.000000000    7  232.41375    FALSE
10  12427   1.4350272 0.7394895  1.8045495 4.527916e+01 1.000000000 1.1024594 0.958904110 1.0164384 0.057534247    2  275.26667     TRUE
11  12429   0.6931753 0.8062314  0.8724209 1.224069e+01 1.000000000 1.0738361 0.975342466 1.0000000 0.024657534    3  937.60000     TRUE
12  12431   3.1719040 1.4533327  3.3128710 9.585705e+01 1.000000000 0.9561497 0.926027397 1.0219178 0.095890411   13  463.38929     TRUE
13  12433   5.1484706 2.5744466  1.2162717 1.523925e+02 1.000000000 1.0747837 1.021917808 1.0219178 0.000000000    5 2229.31167     TRUE
14  12441   0.4854388 2.6115105  0.8520459 2.845405e+00 0.250000000 0.5054921 0.000000000 1.0027397 1.002739726    0  173.55000     TRUE
15  12471   2.3083832 1.6613031  4.2637941 2.326650e+02 1.000000000 0.9820934 0.991780822 0.9972603 0.005479452   19  991.20250    FALSE
16  12472   0.6282756 1.4013803  2.1420961 1.821113e+01 1.000000000 0.9057073 0.923287671 1.0109589 0.087671233    6  938.87286    FALSE
17  12481   1.6455236 1.0489949  0.4748283 2.038658e+01 1.000000000 0.9296181 0.939726027 1.0000000 0.060273973    7  699.54000    FALSE
18  12494   2.3182164 2.1335827  2.1134697 6.099932e+01 1.000000000 1.0223359 0.958904110 1.0000000 0.041095890    5  206.85833     TRUE
19  12515   2.9054662 1.1915621  2.9360445 2.917572e+01 0.000000000 0.4950609 0.000000000 0.9671233 0.967123288    0  383.70000     TRUE
20  12540   1.1118179 2.1854681  2.5775475 1.688938e+01 0.987333333 0.8882369 0.936986301 0.9890411 0.052054795   16  788.24941     TRUE
21  12551   1.7419763 1.4084740  2.2263883 2.997041e+01 0.250000000 0.5117030 0.000000000 0.9780822 0.978082192    0  168.00000     TRUE
22  12557   2.0119643 2.3316576  2.3181907 2.830576e+01 1.000000000 1.0684409 0.972602740 1.0164384 0.043835616    4 2398.19200     TRUE
23  12567   2.2619141 3.1133720  2.2530147 4.519842e+02 0.750000000 1.0957369 0.950684932 1.0109589 0.060273973    8 1012.77111     TRUE

そのため, 他のソフトで計算することも含めて, いろいろ試す必要がありそうだ

まとめ (暫定)

技術面に関して言えば, Stan は使いようによっては数値計算の精度をかなり意識して書かないとダメだと分かってきた. 作業時間の短縮を狙うなら, stan 以外で実装したほうが早かったのではという感じすらある. また時間があるときに推定パートも python で書いてみようと思う. 加えて, データを加工する過程でも, 勉強のためあまり経験のない python (pandas) を利用したの結果、トータルで (データの整合性の確認作業も含めて) おそろしく時間がかかった. もっと経験値が必要なようだ. pandas もオブジェクトの違いがわかりにくく, sqlite でやったほうが早いのではという気がしている. 異なるスタンダードになれるというのも大事だが, pandas と SQL とでは後者のほうが普及しているのでは? pandas の強みって何でしょう?
この手法の実用性について. 個人レベルの顧客生涯価値を計算するのだから, なるべく直近のものまで計算したほうがいいのだが, 観測期間が短くなるほど当然誤差が大きくなるはずだ. 一方で1年も2年も前の顧客の価値しか計算できないようでは即効性のない分析になってしまう. 実用性を考えるなら, 最小でどれくらいの期間あれば使える推定になるかというのは重要になると思うのだが, 今回参照した文献ではその辺には触れられていなかった.
また, 本来は顧客の属性と紐付けて推定するものだが, 先に書いたように今回はそのデータがなかったため断念した. そういうデータがあれば面白い分析が出来そうなのだが, 性質上なかなか手に入らなさそうである.

参考文献

Abe, Makoto. 2009. “‘Counting Your Customers’ One by One: A Hierarchical Bayes Extension to the Pareto/NBD Model.” Marketing Science 28 (3): 541–53. doi:.

Chen, Daqing, Sai Laing Sain, and Kun Guo. 2012. “Data Mining for the Online Retail Industry: A Case Study of RFM Model-Based Customer Segmentation Using Data Mining.” Journal of Database Marketing & Customer Strategy Management 19 (3). Nature Publishing Group: 197–208. doi:Data mining for the online retail industry: A case study of RFM model-based customer segmentation using data mining | SpringerLink.

阿部, 誠. 2004. “CRM のデータ分析に理論とモデルを組み込む – 消費者行動理論に基づいた RF 分析 –.” 流通情報, no. 426: 10—17.

———. 2008. “消費者行動理論にもとづいた個人レベルの RF 分析: 階層ベイズによる Pareto/NBD モデルの改良.” 日本統計学会誌 37 (2): 239—259.

———. 2011. “RFM指標と顧客生涯価値: 階層ベイズモデルを使った非契約型顧客関係管理における消費者行動の分析.” 日本統計学会誌 41 (1): 51—81.

*1:厳密には MCMC じゃなくて HMC を使ったんだけど

*2:ここでは, 顧客ごとの最初の購買から観測終了までの期間を意味する.

*3:階層ベイズ法と銘打っているが, 実際にはむしろ生存期間を潜在変数として扱うというところがこのモデルの重要なところな気がする.

*4:先行研究では正規分布やガンマ分布を仮定していたものもあった.

*5: $x$ が正整数なので厳密にはアーラン分布か.

*6:参考は http://mathworld.wolfram.com/ErlangDistribution.html

*7:未知数はギリシャ文字で書くという原則にしたがって書いているので, 元論文と違う記号になっている.

*8:顧客生涯「価値」であるから本来マージンを求めるのが字義として正しいのだが, 原価やコストがわからないので売り上げ額をそのまま用いる.

*9:stan のバグも絡んでいるらしい

*10:あまりスマートなやり方でない?

*11:UCI の方には 12/31 までの記録とあるが, 実際のデータには 12/9 までしかない. 3週間も一度も注文がないというのは不自然なので, 観測期間の終わりは 12/9 とした.

*12:阿部 (2011) では百貨店の会員情報と紐付けられた購買歴を使っている.

*13:返品の注文 ID は頭に ’C’ がつくため, 注文か返品かの区別はできるが, ’C’ を取った残り部分が注文 ID に対応するわけではない

*14:メモリが足りないので本来は python でやったほうがいいと思うが, なるべく月1のペースでブログを更新するようにしたかった

*15:この辺の例外処理を簡単に書けるようにならないものか……

ill-identified diary

所属組織の見解などとは一切関係なく小難しい話しかしません

[python] [stan] 潜在変数と階層ベイズ法と RFM 分析 [未完成]

概要

モデル

プログラム

用いるデータ

結果

まとめ (暫定)

参考文献